ТЕМА: Основные понятия комбинаторики.
Ответьте на вопросы письменно: (20-25 мин)
Что называют факториалом? (примеры вычисления)
Комбинаторика-это…
Что такое соединения? виды соединений?
Решить задачу 1 и задачу 2 методом подбора!
Часто в математике нужно вычислить произведение натуральных чисел по порядку, начиная с 1. Например, 1*2*3*4*5*6*7 и т.д. Чтобы запись была короче используют знак «!»
Произведением всех натуральных чисел от 1 до n называется факториалом числа n и записывается n!(читается как эн факториал)
n!=1⋅2⋅3⋅...⋅(n−2)⋅(n−1)⋅n
Чему, к примеру, равны 2!, 3!, 4!, 5!, 6! ? Посчитайте в тетради!
2!= … 3!=… 4!=… 5!=… 6!=…
Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.
Комбинаторика – раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составляемой по заданным правилам.
Группы, составленные из каких-либо элементов, называются соединениями.
Различают три вида соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными, а раздел математики, занимающийся их решением, - комбинаторикой.
Рассмотрим три основных вида соединений и формулы вычисления их количества. Для этого сначала рассмотрим 2 задачи, которые помогут нам сосредоточиться на сути новых понятий.
Задача 1. В некотором учреждении имеются две различные вакантные должности, на каждую из которых претендуют три сотрудника: A, B, C. Сколькими способами из этих трех кандидатов можно выбрать два лица на эти должности?
Задача 2. Для участия в соревнованиях требуется выбрать двоих спортсменов из трех кандидатов: A, B, C. Сколькими способами можно осуществить этот выбор?
1) Размещения.
Определение. Размещениями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.
Число размещений из m элементов по n обозначают  (от французского «arrangement» - «размещение») и вычисляют по формуле:
(от французского «arrangement» - «размещение») и вычисляют по формуле:

2) Перестановки.
Определение. Перестановкой из n элементов называют размещение из n элементов по n.
Число перестановок из n элементов обозначается  и вычисляется по формуле:
и вычисляется по формуле:

3) Сочетания.
Определение.
Сочетаниями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m обозначают 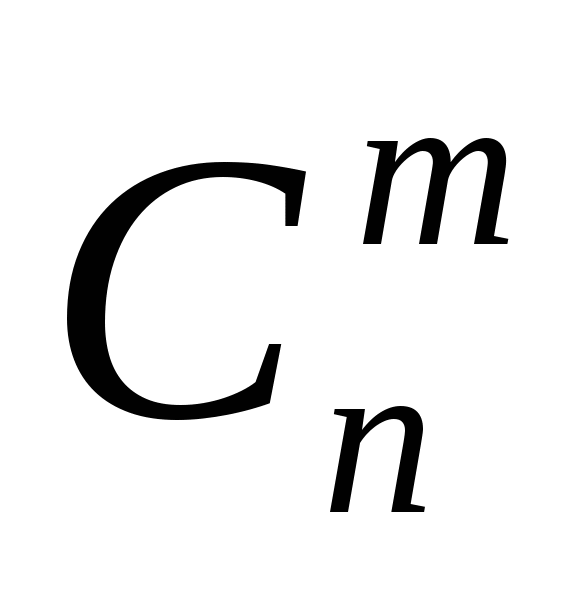 (от французского «combination» - «сочетание») и вычисляют по формуле:
(от французского «combination» - «сочетание») и вычисляют по формуле:

Решение комбинаторных задач.
При решении комбинаторных задач важно научиться различать виды соединений.
Чтобы отличать задачи на подсчёт числа размещений от задач на подсчёт числа сочетаний, определим, важен или нет порядок в следующих выборках:
а) судья хоккейного матча и его помощник;
б) «Шесть человек останутся убирать класс!»
в) две серии для просмотра из многосерийного фильма.
Задача 1. Сколькими способами могут занять I, II, III места 8 участниц финального забега на дистанции 100 м?
Задача 2. Из 30 обучающихся группы надо выбрать старосту и помощника старосты. Сколькими способами это можно сделать?
Задача 3. Сколькими способами можно составить букет из трёх цветков, выбирая цветы из девяти имеющихся?
Задача 4. В группе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Домашнее задание Подготовка сообщений по темам: «Истории комбинаторики», «Комбинаторика и ее применение в реальной жизни».
Проверь себя!
1.Определите вид соединений:
а) Соединения из n элементов, отличающиеся друг от друга только порядком расположения в них элементов, называются __________
б) Соединения из m элементов по n, отличающихся друг от друга только составом элементов, называются _______________
в) Соединения из m элементов по n, отличающихся друг от друга составом элементом и порядком их расположения, называются _________
2.Восстановите соответствие типов соединений и формул для их подсчёта
| 
| А.сочетания |
| 
| В. размещения |
| 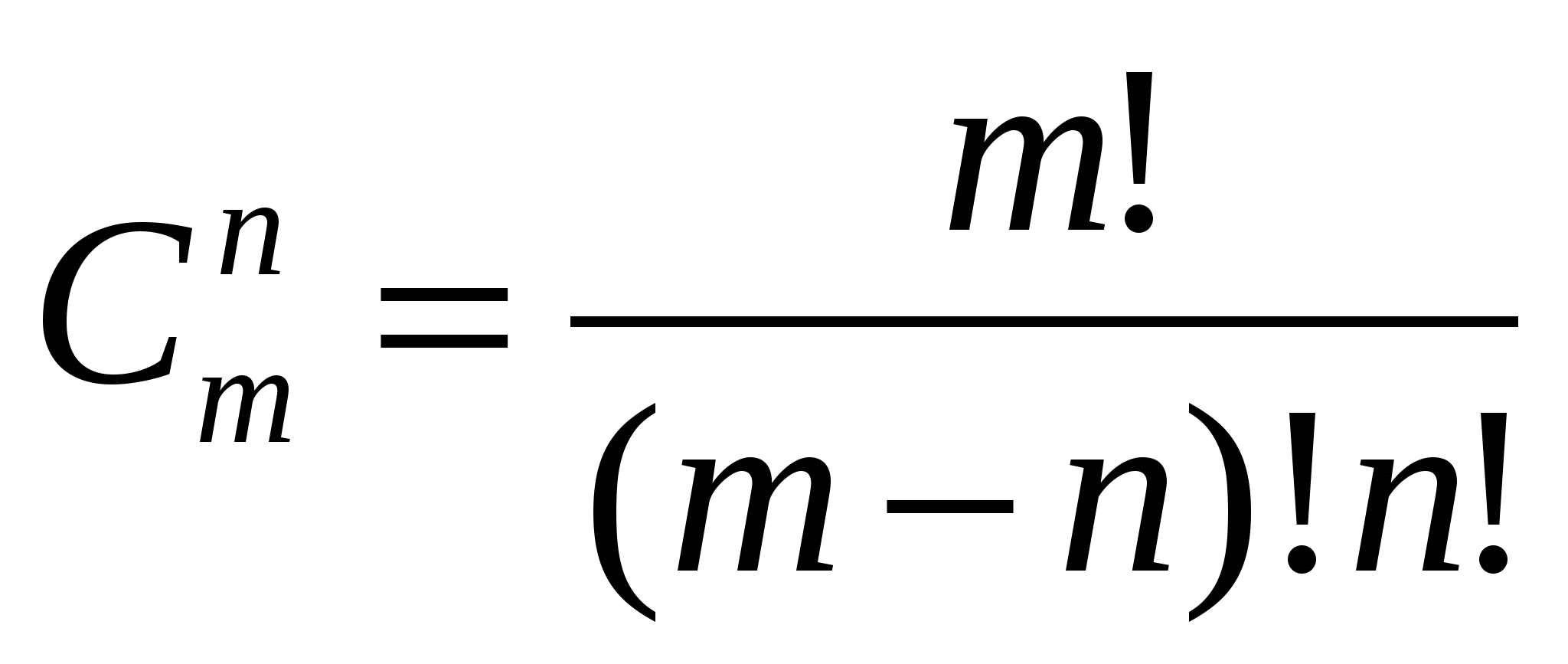
| С. перестановки
|
3. Сколькими способами из класса, где учатся 24 ученика, можно выбрать: а)двух дежурных; б)старосту и помощника старосты?
4. «Проказница Мартышка, Осёл, Козёл да косолапый Мишка задумали сыграть квартет». Сколькими способами они могут выбрать каждый для себя по одному инструменту из 10 данных различных инструментов?







 (от французского «arrangement» - «размещение») и вычисляют по формуле:
(от французского «arrangement» - «размещение») и вычисляют по формуле:









