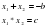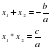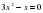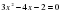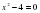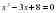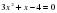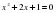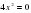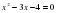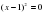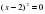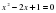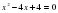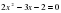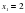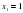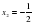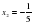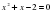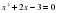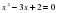1) Обобщить решение квадратных уравнений и закрепить теорему Виета;
2) Углубленное изучение свойств квадратных уравнений;
3) Способствовать выработке у школьников желания в потребности обобщения изучаемых фактов, развивать самостоятельность и творчество.
Просмотр содержимого документа
«Урок алгебры в 8 классе по теме "Квадратные уравнения и теорема Виета".»
2) Урок алгебры в 8 классе
Тема урока: Квадратные уравнения и теорема Виета.
Цель урока:
1) Обобщить решение квадратных уравнений и закрепить теорему Виета;
2) Углубленное изучение свойств квадратных уравнений;
3) Способствовать выработке у школьников желания в потребности обобщения изучаемых фактов, развивать самостоятельность и творчество.
Оборудование: таблица.
Ход урока
I. Задание на дом.
№№ 546(а,б), 587(а,б,в). придумать по 4 уравнения на 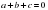
и 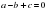 и решить.
и решить.
II. Повторение теоретического материала.
1) Общий вид квадратного уравнения
2) Приведение квадратных уравнений
3) Неполные квадратные уравнения, их решение
4) Что такое дискриминант D для нечетных и d для четных
5) Корни квадратного уравнения
6) Теорема Виета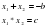
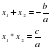
III. Упражнения для повторения (устно).
Что лишнее
1) 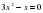
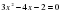
2) 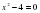
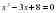
3) 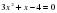
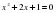
4) 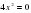
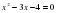
Найти а, b, с, х1+х2, х1*x2. Решить неполные квадратные уравнения
(у доски)
IV.Способы решения полных квадратных уравнений.
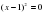
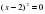
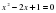
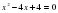
а) Как вообще можно решать квадратные уравнения.
Можно решать выделением квадрата двучлена. Формулами корней квадратного уравнения (а - 5)2 = -4 и используя теорему Виета х2 -6х + 5 = 0 найти х1+х2 и х1*х2. Угадать корни теоремой Виета
б) Решить квадратное уравнение функциями
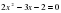

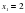
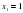
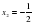
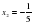
Итак: Мы выяснили, как можно решать квадратное уравнение. Каждый раз решая новым способом мы убеждались, что приходим к более легкому решению. Сегодня мы изучим еще один новый способ для решения некоторых квадратных уравнений. Для этого надо знать некоторые свойства квадратного уравнения.
V. Изучение нового способа.
На доске:
|
| a | b | c | a+b+c | x1 | x2 |
| 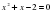
| 1 | 1 | -2 | 0 | 1 | -2 |
| 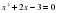
| 1 | 2 | -3 | 0 | 1 | -3 |
| 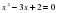
| 1 | -3 | 2 | 0 | 1 | 2 |
| 
| 5 | -8 | 3 | 0 | 1 | 
|
Посмотрите на эти уравнения, взгляните на их корни. Обратите внимание на сумму коэффициентов. Сделайте вывод. Таблица:
№ 534 (а,б,д) из учебника
|
| a | b | c | a+b+c | x1 | x2 |
| 
| 2 | -1 | -3 | 0 | -1 | 
|
| 
| 1 | 5 | 4 | 0 | -1 | -4 |
| 
| -1 | 2 | 3 | 0 | -1 | 3 |
| 
| 5 | 1 | -4 | 0 | -1 | 
|
VI.Закрепление.
Каким способом решаем данное уравнение?
а) 
2+3+1 =0 
б) 
3+1-4=0 
в)
-1-2+3=0 
Как быстрее можно решить данные уравнения?
а)  (5;5)
(5;5)
б)  (2;1)
(2;1)
в)  (-1;4)
(-1;4)
г)  (6;-8)
(6;-8)
д)  (-2;-3)
(-2;-3)
е)  (1;
(1; )
)
ж) 
з) 
Самостоятельная работа
1)  (1;-24)
(1;-24)  (1;-16)
(1;-16)
2)  (1;
(1; )
)  (1;
(1;  )
)
3)  (1;-3)
(1;-3)  (1;-16)
(1;-16)
4)  (-1;-12)
(-1;-12)  (-1;-9)
(-1;-9)
VII Итог урока.







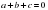
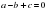 и решить.
и решить.