Урок геометрии в 9 классе
Тема: « Конус
Цели: познакомить учащихся с понятием конуса, его элементами; вывести формулу, выражающую объем конуса и формулу площади боковой поверхности конуса; учить решать задачи; способствовать развитию логического мышления учащихся.
1. Возьмем прямоугольный треугольник АВС и будем вращать его вокруг катета АВ . В результате получится тело, которое называется конусом.
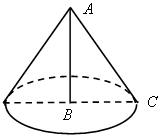
2. Прямая АВ называется осью конуса, а отрезок АВ – его высотой.
При вращении катета ВС образуется круг, он называется основанием конуса. При вращении гипотенузы АС образуется поверхность, состоящая из отрезков с общим концом А Ее называют конической поверхностью или боковой поверхностью конуса, а отрезки, из которых она составлена, – образующими конуса. Таким образом, конус – это тело, ограниченное кругом и конической поверхностью.
3. Пользуясь принципом Кавальери, можно доказать (см. задачу № 1219), что объем конуса равен одной трети произведения площади основания на высоту.
,
где r – радиус основания, h – его высота. 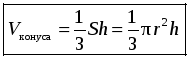
. Ввести понятие развертки боковой поверхности конуса . Развертка боковой поверхности конуса представляет собой круговой сектор. Радиус этого сектора равен образующей конуса, то есть рав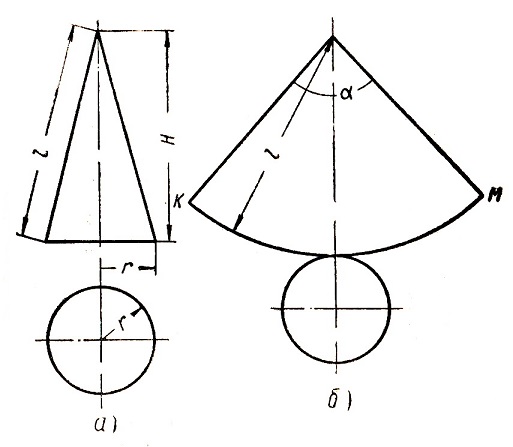 ен l, а длина дуги сектора равна длине окружности основания конуса, то есть равна 2πr.
ен l, а длина дуги сектора равна длине окружности основания конуса, то есть равна 2πr.
5. Площадь Sбок боковой поверхности конуса равна площади ее развертки, то есть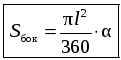 де α – градусная мера дуги сектора (рис. 363, б).
де α – градусная мера дуги сектора (рис. 363, б).
Длина дуги окружности с градусной мерой и радиусом l равна 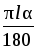 .
.
С другой стороны, длина дуги равна 2πr, то есть 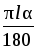 = 2πr, поэтому
= 2πr, поэтому
Sбок = 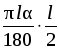 = 2πr ∙
= 2πr ∙ 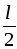 = πrl.
= πrl.
Итак, площадь боковой поверхности конуса с образующей l и радиусом основания r выражается формулой
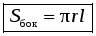 .
.
,
Выполнение упражнений.
1. Решить задачу № 1220 (б, в).
Учащиеся решают самостоятельно, потом решение задачи проверяется.
Решение
б) Дано: r = 4 см; V = 48 π см3. Найти h.
V = 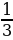 πr2h; отсюда h =
πr2h; отсюда h = = 9 (см).
= 9 (см).
Ответ: 9 см.
в) Дано: h = m; V = р. Найти r.
V = 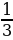 πr2h; найдем r2 =
πr2h; найдем r2 = , тогда r =
, тогда r = .
.
Ответ:  .
.
2. Решить задачу № 1221 на доске и в тетрадях.
Решение
Sосн = Q, Sбок = P. Найти V.
1) Sосн = πr2 = Q, отсюда r = .
.
2) Sбок = πrl = P, отсюда l = .
.

3) По теореме Пифагора из Δ АВС найдем
h2 = l2 – r2 = .
.
Значит, h =  .
.
4) Найдем объем конуса
V =  πr2h =
πr2h = Q ∙
Q ∙  .
.
Ответ:  .
.
3. Решить з 
5. Решить задачу № 1249.
Решение
По условию h = 12 см, V = 324 π см3. Найти α дугу развертки боковой поверхности конуса.
1) V =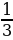 πr2h;
πr2h;
324π =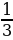 πr2 ∙ 12;
πr2 ∙ 12;
324 = 4r2;
r2 = 81;
r = 9 (см).
2) Sбок = ∙ α = πrl, отсюда, сократив обе части равенства на πl, получим
∙ α = πrl, отсюда, сократив обе части равенства на πl, получим  = r, тогда
= r, тогда  = 9, значит, α =
= 9, значит, α = .
.
3) l2 = h2 + r2, то l = = 15 (см).
= 15 (см).
4) α = = 216°.
= 216°.
Ответ: α = 216°.
. Итоги урока.
Домашнее задание: изучить материал пункта 130; ; решить задачу № 1220 (а); записать в тетрадь решение задачи № 1222








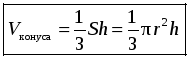
 ен l, а длина дуги сектора равна длине окружности основания конуса, то есть равна 2πr.
ен l, а длина дуги сектора равна длине окружности основания конуса, то есть равна 2πr.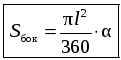 де α – градусная мера дуги сектора (рис. 363, б).
де α – градусная мера дуги сектора (рис. 363, б).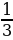 πr2h; отсюда h =
πr2h; отсюда h = = 9 (см).
= 9 (см).










