Урок-игра "Лучший знаток математики"

Урок - игра «Лучший знаток математики»

Внеклассное мероприятие

по математике

для учащихся 8 класса

Цель мероприятия: через занимательные упражнения содействовать повышению интереса учащихся к математике; развивать логическое мышление, внимание, сообразительность.

Оборудование: листы с заданиями, листы с вариантами ответов, 8 наборов карточек с цифрами от 1 до 4; секундомер, метроном, призы

Подготовительная работа

Учитель предварительно ознакомил класс с условиями игры; предупредил о том, какие темы будут вынесены для закрепления, разбил класс на команды (4 участника + 4 ученика в "группе поддержки" на каждую тему).

На перемене, перед началом игры, ученики передвигают парты к задней стене класса. Перед доской освобождается место для основных участников. На полу отмечаются мелом линии. Приглашаются ученики 9 класса – эксперты. Они наблюдают за временем, музыкальным оформлением, правильностью ответов; ведут подсчет баллов.

Правила игры

Приглашаются 7 ученика – основные участники и 4 ученика – " группа поддержки". Основные участники становятся у черты лицом к доске, спиной к классу и "группе поддержки" ("группа поддержки" за первыми партами). Учитель сообщает тему. Один из учеников класса кратко сообщает исторические сведения по теме. Далее предлагаются задания и 4 ответа к каждому. Ученик – участник игры должен за определенное время, отсчитываемое метрономом, найти правильный ответ и поднять карточку с соответствующей цифрой (номер по порядку ответов). Те же задания выполняют ученики из "группы поддержки" и поднимают свои карточки.

За правильный ответ ученик получает 1 балл и делает шаг вперед. Если совпали правильные ответы у основного участника и "поддерживающего", то основному участнику добавляется еще 1 балл.

Победит тот, кто наберет больше баллов. Он выходит в финал.

Затем объявляется новая тема. Выходят новые участники. Игра продолжается.

Затем финал и чествование победителя. В ходе игры учитель может спросить ответ у любого ученика, поэтому задания решают все.

Кроме того, для поддержания интереса, помимо учебных заданий, даются задания на составление слов (подобно тому, как это делается в телеигре "Звездный час"), задачи на смекалку. Например, из букв слова "планиметрия" составить как можно больше слов.

Задания по теме "Функции"

1. Какая из формул задает функцию "обратная пропорциональность":

а) y = kx + b; б) в) ; г)

2. В каких координатных четвертях расположен график функции

при k

а) I и II; б) I и III; в) I и IV; г) II и IV

3. Укажите область определения функции у =

а) х – любое число, кроме 0 и 2; б) х – любое число;

в) х – любое число, кроме ± 1; г) х – любое число, кроме 0

4. Дан график функции (см. рис). Как записывается уравнение этой функции:

у

1

0 х

а) y = 2x; б) в) y = 2 - x; г)?

5. Даны графики функций и их уравнения. Но не все уравнения соответствуют графикам. Какие уравнения надо переставить?

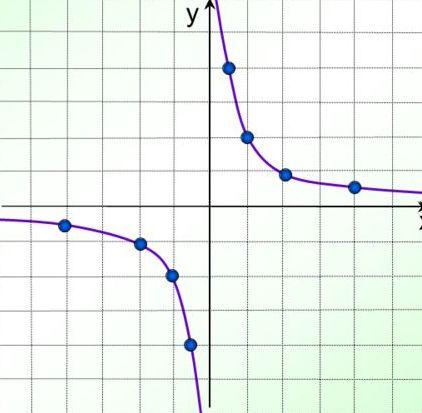
а) ; б) х³;

;

в)

г) y = 2x

"Степень с целым показателем"

1. Значение выражения равно:

а) 1; б) 2⁴ =16; в) = ; г)

2. Значение выражения

равно:

а) 2 ^-1= ; б) 1; в) 2⁶ = 64; г) 2¹= 2

3. Как записать число 2 180 000 в стандартном виде:

а) 218 · 10⁴; б) 2,18 · 10⁶; в) 2,18 · 10⁷; г) 21,8 · 10⁵?

4. Число 0,0000035 в стандартном виде записывается так:

а) 35 · 10^-7; б) 35 · 10^-5; в) 3,5 · 10^-6; г) 3,5 · 10⁶?

5. Вычислите 10⁰: 10^-3

а) =1000; б) = ; в) 10⁰ =1; г) =10 000?

"Четырехугольники"

1. Один из четырехугольников лишний, т.е. не удовлетворяет некоторому условию. Какой?

а) б)

в) г)

2. Какому из древних ученых принадлежит утверждение: квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов:

а) Архимед; б) Пифагор; в) Фалес; г) Евклид?

3. Кто из древних ученых создал руководство по математике под названием "Начала":

а) Архимед; б) Пифагор; в) Фалес; г) Евклид?

4. На каком рисунке заштрихованы равные треугольники?

а) б)

в)

г)

5. Кто является автором вашего учебника "Геометрия":

а) Фалес; б) Погорелов; в) Атанасян; г) Евклид?

Можно подобрать подобные задания к другим темам, изученным в течение года (или семестра).

Краткие исторические сведения

Функции

Еще задолго до того, как сформировались общие понятия переменной величины и функции, они фактически использовались в математике.

Термин "функция" ввел немецкий математик Г.Лейбниц (1646 – 1716 г.г.). У него функция связывалась с графиком.

Термин "функция" происходит от лат. functio – деятельность, выполнение

Степени

Понятие степени с натуральным показателем сформировалось еще у древних народов. Квадрат и куб числа использовали для вычисления площадей и объемов. Степени некоторых чисел использовались при решении отдельных задач учеными Древнего Египта и Вавилона.

В конце XVI века Франсуа Виет ввел буквы для обозначения в уравнениях не только неизвестных, но и их коэффициентов. Он применял сокращения:

N (Numerus – число) – для первой степени,

Q (Quadratus – квадрат) – для второй,

C (Cubus – куб) – для третьей,

QQ – для четвертой и т.д.

Современные определения и обозначения степени с нулевым, отрицательным и дробным показателем берут начало от работ английских математиков Д.Валлиса (1616 – 1703 г.г.) и И.Ньютона (1643 – 1727 г.г.)

3