ТЕМА Что такое функция. РЕАЛЬНЫЕ ЗАВИСИМОСТИ.
Цели: ввести понятие функциональной зависимости; дать определения независимой переменной (аргумента), зависимой переменной, области определения функции, области значений функции.
Ход урока
Организационный момент
I. Устная работа.
1. Найдите значение выражения.
а) 3x – (2 + 3x) при х = 7,862; б) 2a – (a – 0,3) при а = 0,7;
2. Решите уравнение.
а) 3х = –9; б) 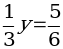 ; в) 5а – 15 = 0; г) 3х = 3х + 11; д)
; в) 5а – 15 = 0; г) 3х = 3х + 11; д) 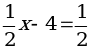 (x – 8); е) 3y +
(x – 8); е) 3y + 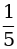 = 0.
= 0.
II. Объяснение нового материала.


 III. Формирование умений и навыков.
III. Формирование умений и навыков.
Все задания, решаемые на этом уроке, направлены на усвоение как самого понятия функции, так и различных способов её задания (словесный, с помощью формулы, табличный, графический). Ученики должны уметь переходить от одного вида задания к другому и находить значения функции при каждом способе задания.


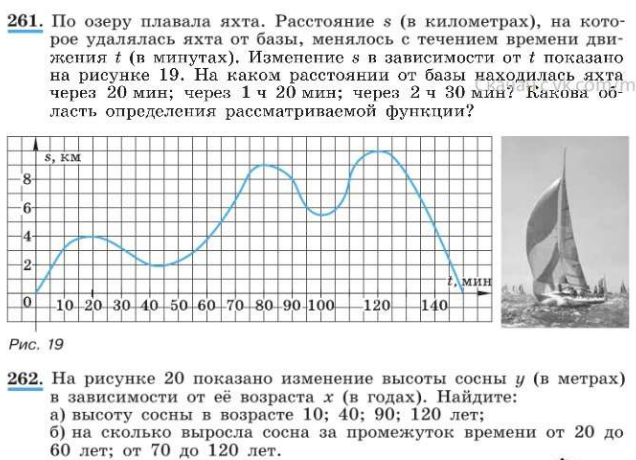
Задача Функция задана графиком:
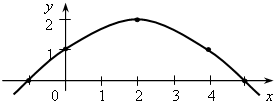
а) Найти значения функции при х = 0; 2; 3,5; –1.
б) При каком значении х значение функции равно 1; 2; 0?
в) Назвать несколько значений х, при которых значение функции положительно.
г) Назвать несколько значений х, при которых значение функции отрицательно.
Устная работа
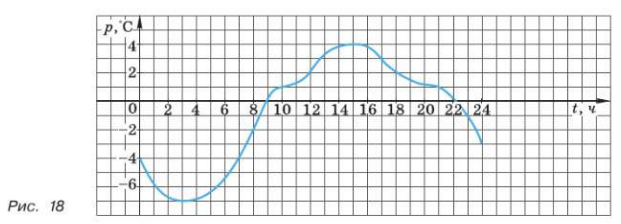
Результаты измерений температуры воздуха за сутки даны в следующей таблице:
| Время, ч | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| Температура, °С | –1 | +1 | –3 | –4 | 2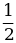 | 5 | 8 | 10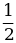 | 11 | 9 | 6 | 3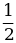 | 1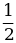 |
а) Назовите температуру в 6 ч, 8 ч, 24 ч.
б) В какое время температура была равна +1°, –4°, 11°?
в) Почему эту зависимость можно назвать функцией?
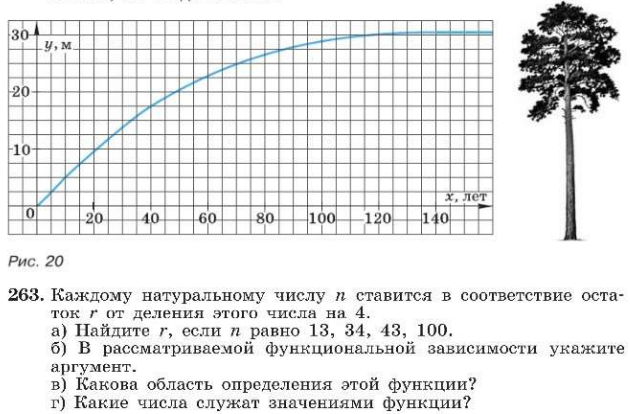
Решение:
Если r – остаток от деления натурального числа п на 4, то можно записать n = 4 · x + r, где 0 ≤ r
Найдем соответствующие значения r:
а) Если п = 13, то 13 = 3 · 4 + 1, то есть r = 1;
б) если п = 34, то 34 = 8 · 4 + 2, то есть r = 2;
в) если п = 43, то 43 = 10 · 4 + 3, то есть r = 3;
г) если п = 100, то 100 = 25 · 4 + 0, то есть r = 0.
В рассматриваемой функциональной зависимости аргументом является переменная п.
Областью определения является множество чисел {13; 34; 43; 100}.
Значениями функции служат числа 0; 1; 2; 3.
IV. Итоги урока. Рефлексия.
– Что называется функцией?
– Что называется аргументом?
– Какими способами можно задать функцию? Назовите преимущества каждого из них.
Домашнее задание:
1. Решите №№ № 259; № 262; № 264.



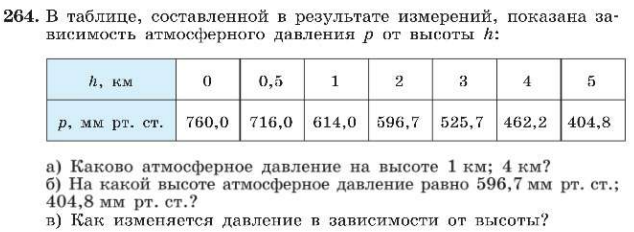
2. ЗАДАЧА. Функция задана графиком:
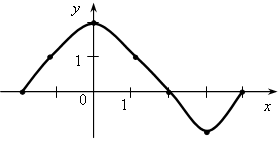
а) Найти значения функции при значениях аргумента 0; –2; 1; 3.
б) При каком значении х значение функции равно 2; 0; 1; –1?
в) Назвать несколько значений х, при которых значение функции положительно.
г) Назвать несколько значений х, при которых значение функции отрицательно.
ТЕМА Вычисление значений функции по формуле
Цели: продолжить работу по усвоению понятия функции и связанных с функцией понятий (область определения функции, область значений функции и др.); формировать умение находить значения функций, заданных аналитически (с помощью формулы).
Ход урока
I. Организационный момент
Устная работа.
1. Задайте формулой функцию, сопоставляющую каждому числу третью степень этого числа; сумму этого числа с числом 5.
2. Велосипедист едет со скоростью 15 км/ч и за t ч проходит расстояние s км (зависимость s от t). Найдите значение функции, соответствующее значению аргумента, равному 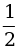 ; 2; 2
; 2; 2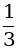 .
.
II. Объяснение нового материала.
Чаще других в математике и её приложениях применяется задание функции формулой. Все другие способы играют подчиненную роль. Однако сопоставление разных способов задания выполняет важную роль:
1) и таблицы, и графики служат для удобного в определенных обстоятельствах представления функции, имеющей аналитическую форму записи;
2) необходимо для усвоения всего многообразия аспектов понятия функции.
Разбираем пример № 1 со с. 55 учебника. Показываем, что для того, чтобы найти значение функции, необходимо подставить некоторое значение аргумента в формулу.


Также объясняем, что в случае, когда х или область определения функции явно не задана, считают, что она состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

III. Формирование умений и навыков.
Групповая работа
1-я группа.
1. 
2. Вычислить значение следующих функций при х, равном –2; –1; 0; 1; 2.
а) у = 3х; б) у = –2х; в) у = –х – 3; г) у = 20х + 4.
2-я группа.
1. № 270. 2. № 271.
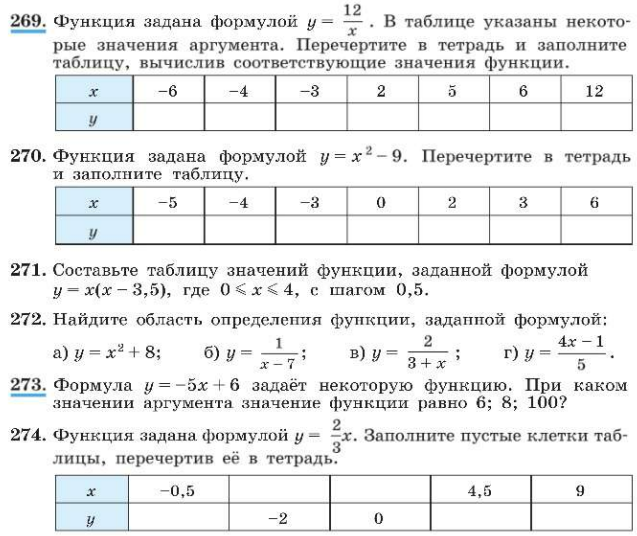
Решение:
у = х (х – 3,5)
| х | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
| у | 0 | –1,5 | –2,5 | –3 | –3 | –2,5 | –1,5 | 0 | 2 |
1. Найдите область определения функции, заданной формулой:
а) у = 3х + 2; б) у = 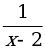 ; в) у = x7 + 2x – 3; г) у =
; в) у = x7 + 2x – 3; г) у = 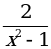 ; д) у =
; д) у = 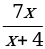 ; е) у =
; е) у = 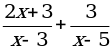 .
.
2. № 351.Решение:
а) у = 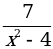 . Область определения функции – все числа, кроме тех, при которых х – 4 = 0, то есть х2 = 4. Значит, не входят в ООФ х = 2 и х = –2.
. Область определения функции – все числа, кроме тех, при которых х – 4 = 0, то есть х2 = 4. Значит, не входят в ООФ х = 2 и х = –2.
б) у = 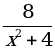 . Область определения функции – все числа, кроме тех, при которых х2 + 4 = 0, то есть х2 = –4. Уравнение не имеет решения, значит, ООФ – любое число.
. Область определения функции – все числа, кроме тех, при которых х2 + 4 = 0, то есть х2 = –4. Уравнение не имеет решения, значит, ООФ – любое число.
Ответ: а) любое число, кроме 2 и –2; б) любое число.
3. Дополнительные задания (для сильных учащихся).
3.1. Найдите область определения функции.
а) у = 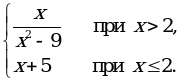 б) у =
б) у = 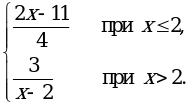
3.2. Задайте формулой какую-нибудь функцию, область определения которой:
а) все действительные числа;
б) все действительные числа, кроме –11;
в) все действительные числа, кроме 3 и 5;
г) все неотрицательные действительные числа;
д) все неположительные действительные числа.;
е) только одно число.
IV. Проверочная работа.
| Вариант 1 | Вариант 2 |
| 1. Дана функция у = 2х2 – 4х. Найдите значение функции при х = 0
и х = –1. 2. Найдите область определения функции. а) у = 2х – 7; б) у = 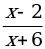 ; ; | 1. Дана функция у = 5х2 + х. Найдите значение функции при х = 0
и х = 1. 2. Найдите область определения функции. а) у = 3х + 6; б) у = 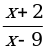 ; ;
|
V. Итоги урока. Рефлексия.
VI. Домашнее задание: № 268; № 269; № 272.



Вычисление значений функции по формуле
Цели: продолжить формировать умение находить значение функции по формуле, а также формировать умение находить значение аргумента, соответствующее заданному значению функцию, умение решать практические задачи с использованием функциональной терминологии.
Ход урока
I. Организационный момент
Устная работа.
1. Найдите значение функции у = 2х – 1 для значений аргумента, равного 0; 1; 2; –1.
2. Найдите область определения функции:
а) у = 3х – 7; б) у = 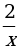 ; в) у = x3 – 2x2 – 1; г) у =
; в) у = x3 – 2x2 – 1; г) у = 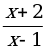 ;
;
II. Формирование умений и навыков.
1. № 273, № 274.
 2. Функция задана формулой у = 2х – 1.
2. Функция задана формулой у = 2х – 1.
а) Какое значение у соответствует х, равному 10; –4,5; 15; 251; 600?
б) При каком значении х соответствующее значение у равно: –19; –57; 205; –3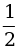 ?
?
Решение:
а) Если х = 10, то у = 2 · 10 – 1 = 19;
если х = –4,5, то у = 2 · (–4,5) – 1 = –10;
если х = 15, то у = 2 · 15 – 1 = 29;
если х = 251, то у = 2 · 251 – 1 = 501;
если х = 600, то у = 2 · 600 – 1 = 1199.
б) Если у = –19, то 2х – 1 = –19;
2х = –19 + 1;
2х = –18;
х = –9; то есть у = –19, при х = –9.
Если у = –57, то 2х – 1 = –57;
2х = –57 + 1;
2х = –56;
х = – 28, то есть у = –57 при х = – 28.
Если у = 205, то 2х – 1 = 205;
2х = 205 + 1;
2х = 206;
х = 103, то есть у = 205 при х = 103.
Если у = –3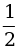 , то 2х – 1 = –3
, то 2х – 1 = –3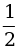 ;
;
2х = –3,5 + 1;
2х = –2,5;
х = –1,25, то есть у = –3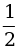 при х = –1
при х = –1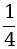 .
.
3. Из формулы равномерного движения s = υt выразить скорость υ как функцию пути s и времени t. Вычислить по этой формуле среднюю скорость полета пули, если s = 3 км, t = 6 с.
4.  Решение:
Решение:
Обозначим за т массу пробки в граммах, а за V – объем в см3. Тогда зависимость массы куска пробки от объема можно выразить формулой т = 0,18 · V.
а) Если V = 240, то т = 0,18 · 240 = 43,2 (г);
б) если т = 64,8, то 0,18 · V = 64,18;
V = 64,18 : 0,18;
V = 360 (см3).
Ответ: а) 43,2 г; б) 360 см3.
5.  Решение:
Решение:
Анализ условия: 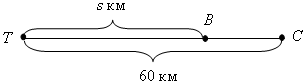
s = 12 · t.
а) Если t = 3,5, то s = 12 · 3,5 = 42 (км);
б) если s = 30, то 12 · t = 30;
t = 30 : 12;
t = 2,5 (ч).
Ответ: а) 42 км; б) 2,5 ч.
6. № 352.Решение:
Анализ условия: 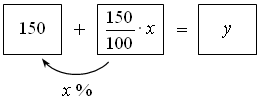
у = 1,5х + 150.
а) если х = 10, то у = 1,5 · 10 + 150 = 15 + 150 = 165;
б) если у = 180, то 1,5х + 150 = 180;
1,5х = 180 – 150;
1,5х = 30;
х = 30 : 1,5;
х = 20, значит, у = 180 при х = 20.
Ответ: а) у = 165; б) х = 20.
III. Проверочная работа.
Вариант 1
1. Функция задана формулой у = 3х – 7. Найдите значение аргумента, при котором значение функции равно нулю.
2. Найдите значение аргумента, при котором функция у = –3х – 2 принимает значение 0,3.
3. Запишите область определения функции, заданной формулой
у = 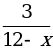 .
.
Вариант 2
1. Функция задана формулой у = 5 + 2х. Найдите значение аргумента, при котором значение функции равно нулю.
2. Найдите значение аргумента, при котором функция у = –5х + 11 принимает значение 0,2.
3. Запишите область определения функции, заданной формулой
у = 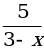 .
.
IV. Итоги урока. Рефлексия.
– Дайте определение функции. Что называется аргументом, значением функции?
– Объясните на примере функции, заданной формулой у = 3х + 18
Домашнее задание: № 275; № 277; № 279; № 353.













 III. Формирование умений и навыков.
III. Формирование умений и навыков.








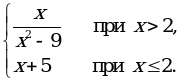 б) у =
б) у = 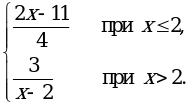


 Решение:
Решение:











