Урок: " Квадратичная функция и её график"

Раздел 8.3A: Квадратичная функция

Школа: Назарбаев Интеллектуальная школа химико-биологического направления г. Петропавловска

Дата:

Ф.И.О. Шарипова АС

КЛАСС: 8

Количество присутствующих:

отсутствующие:

Тема урока:

Квадратичная функция и ее график.

Цель (цели) обучения, на что направлен урок

8.5.1.4 находить значения функции по заданным значениям аргумента и обратно;

8.5.1.5 устанавливать связи между коэффициентами а, b, с квадратичной функции и расположением ее графика на координатной плоскости.

Цели урока

Учащийся знает алгоритм построения графика квадратичной функции;

Учащийся умеет строить график квадратичной функции.

Критерии оценивания

• Уметь находить координаты вершины параболы, зная и используя формулы координат вершины параболы;

• Уметь располагать ветви параболы в зависимости от знака старшего коэффициента;

• Уметь использовать симметрию параболы;

• Уметь строить график функции по найденным точкам.

Языковая цель

Лексика/терминология:

Квадратичная функция, парабола, выделение полного квадрата, ось симметрии, координаты вершины параболы, старший коэффициент, алгоритм построения.

Развитие навыков

Коммуникативные навыки:

1. Работа в парах. Кластер.

Привитие

ценностей

Связи с ценностями НИШ:

• Способствовать самореализации учащихся, способности самостоятельно ставить перед собой цели и реализовывать их.

• Развитие математической грамотности, через умение правильно использовать термины на уроках, словесно комментировать выполняемые упражнения.

Ценности ГГ:

• Воспитание общечеловеческих ценностей: культуры поведения, доброжелательности, взаимовыручки через создание коллоборативной среды на уроке.

• Воспитание аккуратности, трудолюбия, ответственности, самостоятельности через создание проблемных ситуаций на уроке, выполнения задач исследовательского, творческого характера, практико –ориентированных задач.

Межпредметные связи

Навыки использования ИКТ

Умение использовать интерактивную доску, использовать программу «Графический калькулятор».

Предварительные знания

Знают, как строить график квадратичной функции с помощью параллельного переноса и по алгоритму.

План

Запланированные этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

0 –5 мин

Вызов.

1. ФИЗМИНУТКА .

1. Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 10 раз.
2. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 10 раз.
3. Медленно наклоняйте голову: вперед—влево— вправо - назад. Повторите 10 раз.
4. Поморгайте несколько раз глазами, не напрягая мышц.

Сделайте глубокий вздох и медленный выдох.

Здравствуйте.Садитесь.

1. ОПРЕДЕЛЕНИЕ ТЕМЫ И ЦЕЛЕЙ УРОКА.

-совместно с учащимися определить тему урока;

Запишите дату и тему урока в тетрадь.

- совместно с учащимися определить цели урока;

- совместно с учащимися определить критерии оценивания.

Цели урока и критерии оценивания записать на доске.

РРТ

Середина урока

23мин

1. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА.

Работа в парах

кластер

Итак, функция вида y = ax² + bx + c называется квадратичной, графиком ее является парабола. Как следует из названия, главным слагаемым является ax². То есть а не должно равняться нулю, остальные коэффициенты (b и с) нулю равняться могут.

            Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов.

            Самая простая зависимость для коэффициента а. Большинство школьников уверенно отвечает: " если а  0, то ветви параболы направлены вверх, а если а а  0.

y = 0,5x² - 3x + 1

В данном случае а = 0,5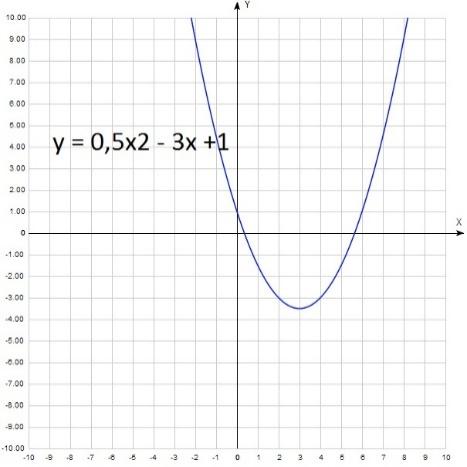

А теперь для а 

y = - 0,5x2 - 3x + 1

В данном случае а = – 0,5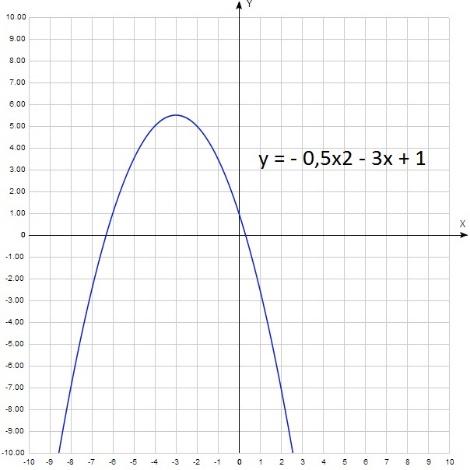

            Влияние коэффициента с тоже достаточно легко проследить. Представим, что мы хотим найти значение функции в точке х = 0. Подставим ноль в формулу:

y = a 0² + b 0 + c = c. Получается, что у = с. То есть с – это ордината точки пересечения параболы с осью у. Как правило, эту точку легко найти на графике. И определить выше нуля она лежит или ниже. То есть с  0 или с 

 с  0: 

y = x² + 4x + 3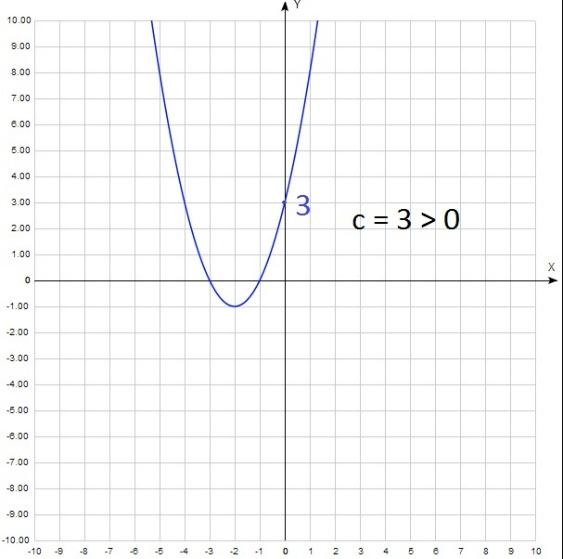

с 

y = x² + 4x – 3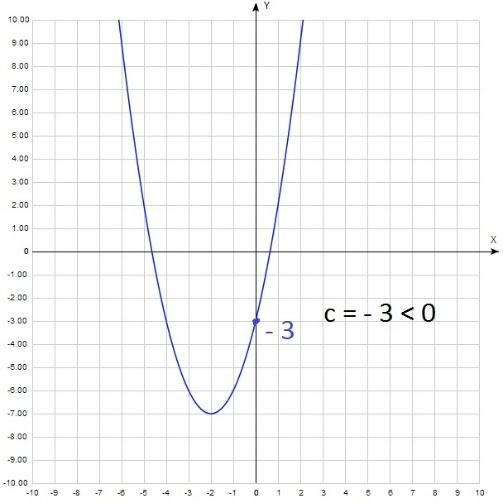

Соответственно, если с = 0, то парабола обязательно будет проходить через начало координат:

y = x² + 4x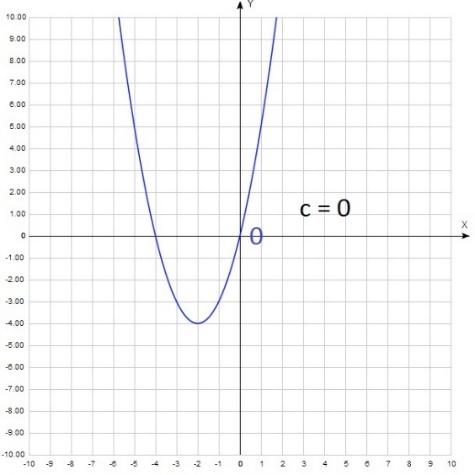

Сложнее с параметром b. Точка, по которой мы будем его находить, зависит не только от b но и от а. Это вершина параболы. Ее абсцисса (координата по оси х) находится по формуле х_в = - b/(2а). Таким образом, b = - 2ах_в. То есть, действуем следующим образом:  на графике находим вершину параболы, определяем знак ее абсциссы, то есть смотрим правее нуля (х_в  0) или левее (х_в 

            Однако это не все. Надо еще обратить внимание на  знак коэффициента а. То есть посмотреть, куда направлены ветви параболы. И только после этого по формуле b = - 2ах_в определить знак b.

Рассмотрим пример: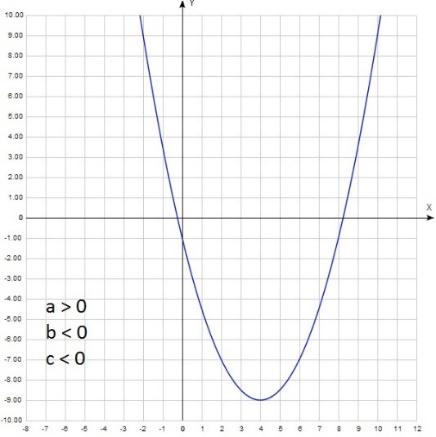

Ветви направлены вверх, значит а  0, парабола пересекает ось у ниже нуля, значит с х_в  0. Значит b = - 2ах_в = -++ = -. b а  0, b с 

Рассмотрим еще один график: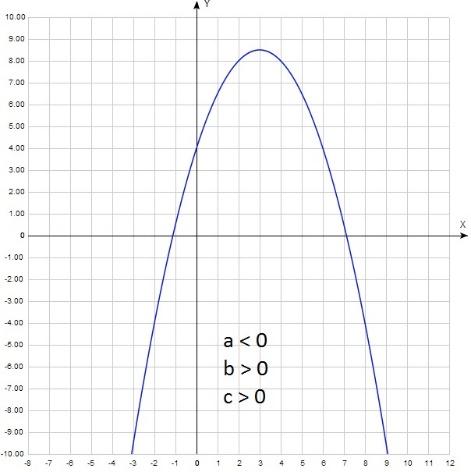 

Ветви направлены вниз, значит а с  0, вершина параболы лежит правее нуля. Следовательно, х_в  0. Значит b = - 2ах_в = --+ = +. b  0. Окончательно имеем:     а b  0, с  0.

А теперь такой: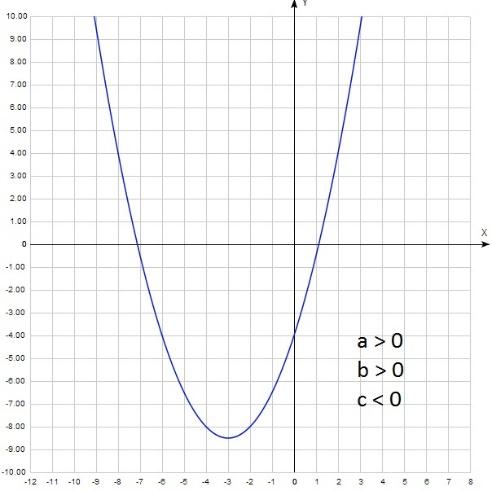

Ветви направлены вверх, значит а  0, парабола пересекает ось у ниже нуля, значит с х_в b = - 2ах_в = -+- = +. b  0. Окончательно имеем:     а  0, b  0, с 

Если b = 0, то вершина параболы лежит на оси у. Она может лежать выше нуля (с  0)

y = x² + 3: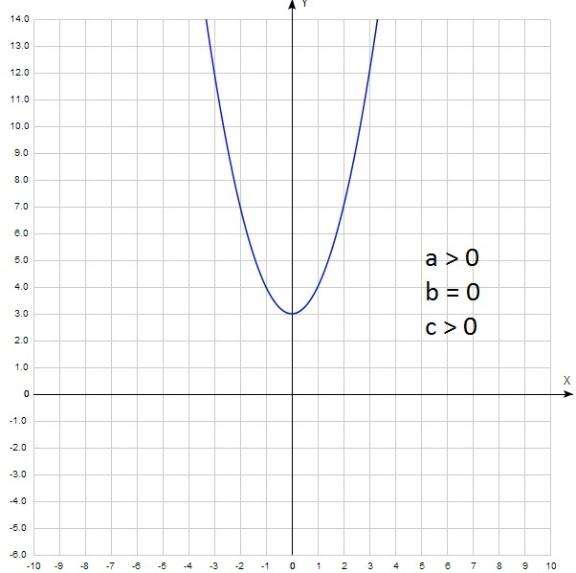

Или ниже нуля  (с у:

y = x² - 4: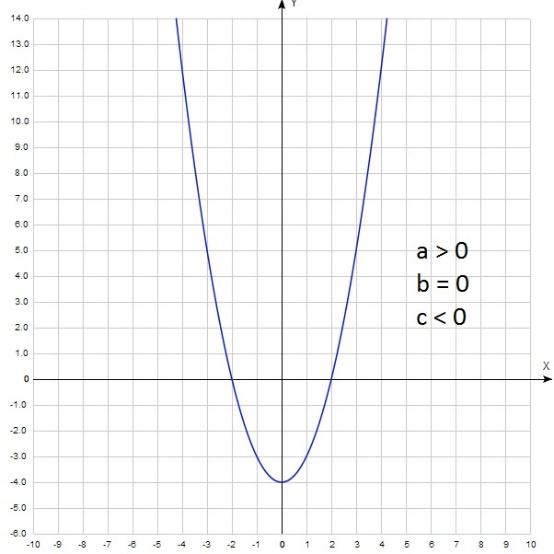

Раздаточный материал

Устная работа.

Определите, график какой функции изображен на рисунке:

PPT

Устно

По графику функции у = ах² + bх + с определите знаки коэффициентов а, b и с:

а)

б)

Р е ш е н и е

а) Ветви параболы направлены вверх, поэтому а 0.

Парабола пересекает ось ординат в нижней полуплоскости, поэтому с b воспользуемся формулой для нахождения абсциссы вершины параболы: т = . По графику видно, что т а 0. Поэтому b 0.

б) Аналогично определяем знаки коэффициентов а, b и с:

а с 0, b

Письменно в тетради

ФО №3

1. По графику функции у = ах² + bх + с определите знаки коэффициентов а, b и с:

Ответ: , , .

2. По графику функции у = ах² + bх + с определите знаки коэффициентов а, b и с:

Ответ:  , , .

3.При каком значении аргумента значение функции

равно 0?

Решение:

При y=0

Решаем квадратное уравнение.

4. Найдите значение функции при х=2.

Рефлексия

2 мин

Как влияют коэффициенты а, b и с на расположение графика квадратичной функции?

Д/з

1 мин

1) График какой из функций изображен на рисунке

Дополнительная информация

Дифференциация - как вы планируете оказывать больше поддержки? Как вы планируете давать задания более способным учащимся?

Дифференциация на уроке основана на принципах проблемного обучения и самостоятельного открытия знаний при изучении нового материала, а так же заданий более высокого уровня сложности на этапе закрепления.

Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?

При объяснении нового материала самооценивание по готовым ответам учащихся и словесное оценивание учителем, при первичном закреплении материала самооценивание по листу с готовым решением.

На этапе закрепления самооценивание по чертежу построенному на компьютере.

Здоровье и соблюдение техники безопасности

Физминутка в начале урока. Повторение правил ТБ при работе с ноутбуками.

Рефлексия по уроку

Были ли цели урока/цели обучения реалистичными?

Все ли учащиеся достигли ЦО?

Если нет, то почему?

Правильно ли проведена дифференциация на уроке?

Выдержаны ли были временные этапы урока?

Какие отступления были от плана урока и почему?

Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.

Цели урока были реалистичными, так как учащимся удалось самостоятельно вывести формулы и составить алгоритм построения графика квадратичной функции.

Конечно, были учащиеся которые не совсем поняли материал, но тема имеет продолжение на следующем уроке.

Дифференциация для учащихся при изучений нового материала была предусмотрена в виде задания более высокого уровня сложности, в котором необходимо было синтезировать знания из предыдущих тем с новым материалом и провести анализ при решении задачи.

Временные рамки были выдержаны.

Отступлении от плана урока не было.

Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?

1: Удачным была постановка вызова в начале урока .

2: Самостоятельное исследование учащимися поставленной задачи и самостоятельное составление алгоритма построения графика квадратичной функции..

3 .Использованеие ИКТ при проверке заданий

Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?

1: Больше времени уделить на рефлексию. Каждый ученик должен осознать, какое значение урок имел лично для него и записать это.

Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?

В классе есть учащиеся у которых задания более высокого уровня сложности вызывают интерес и повышают мотивацию к учению, но и есть учащиеся которым необходима поддержка.