Урок по алгебре в 8 классе по теме
«Понятие квадратного арифметического корня
из неотрицательного числа»
Цель урока: дать понятие о корне из числа, научить находить 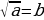 по определению.
по определению.
Задачи урока:
Повторить и закрепить знания учащихся об рациональных числах.
Ввести понятие квадратного корня их неотрицательного числа а и определение арифметического квадратного корня из числа а.
Закрепить эти понятия в ходе выполнения упражнений.
Рассмотреть правила вычисления квадратного корня из неотрицательного числа.
Формировать умение вычислять квадратный корень из чисел и выражений.
Развивать логическое мышление учащихся.
Вырабатывать навыки устного счета.
План урока:
Организационный момент (1 минута).
Актуализация опорных знаний учащихся (5 минут).
Объяснение нового материала (10 минут).
Закрепление нового материала (20 минут).
Итог урока (2 минуты).
Домашнее задание (2 минуты).
Ход урока
Организационный момент.
Подготовка учащихся к работе на занятии, приветствие.
Актуализация опорных знаний учащихся.
1. Что называется степенью числа с натуральным показателем? Основанием степени? Показателем степени?
Представить в виде степени:
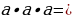
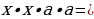
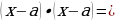
Вычислить:
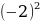 =
= 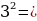
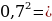
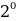 =
= 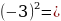
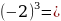
2. Найти значение 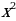 при х = 3; х = 4; х = - 5; х = 0; х =
при х = 3; х = 4; х = - 5; х = 0; х = 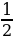 ; х = - 4 .
; х = - 4 .
3. Решить уравнение:
а) 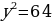 б)
б) 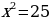 в)
в) 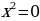
Объяснение нового материала.
Учитель объясняет тему согласно параграфу учебника. Учащимся в тетрадь надо вписать определения квадратного корня, подкоренного числа, извлечения квадратного корня.
1). Вводная беседа.
Мы повторили понятие степени с натуральным показателем. Оно является таким же действиям как сложение, умножение, вычитание и деление. Каждое из них имеет обратное действие. Сложение – вычитание, умножение – деление. Действие – возведение в степень тоже имеет обратное. Давайте попробуем найти его.
Для этого рассмотрим задачу на нахождение площади квадрата.
2). Введение определения.
Решим задачу:
| 1. Нахождение площади квадрата по стороне | 2. Нахождение стороны по площади квадрата |
| 
а а = 3, 8, 10, 25. S = ? | 
а S = 4; 25; 81; 121; 400; 50. а = ? |
Определение: Квадратным корнем из числа а называют число, квадрат которого равен числу а.
Число 7 и -7 – являются корнями уравнения x2 = 49. И оба при возведении в квадрат дают 49. Но сторона квадрата может быть только числом неотрицательным.
Определение: Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен числу а.
Арифметический квадратный корень обозначается значком 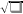 - радикал, корень.
- радикал, корень.
Это число обозначают 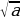 , число а при этом называют подкоренным выражением.
, число а при этом называют подкоренным выражением.
Пример: 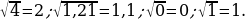
Записать в тетрадь:
Равенство 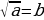 является верным, если выполняются два условия:
является верным, если выполняются два условия:
1) b ≥ 0, 2) b² = а.
При а 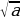 не имеет смысла. Действительно, квадрат любого числа есть число неотрицательное. Например, не имеют смысла выражения
не имеет смысла. Действительно, квадрат любого числа есть число неотрицательное. Например, не имеют смысла выражения 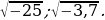
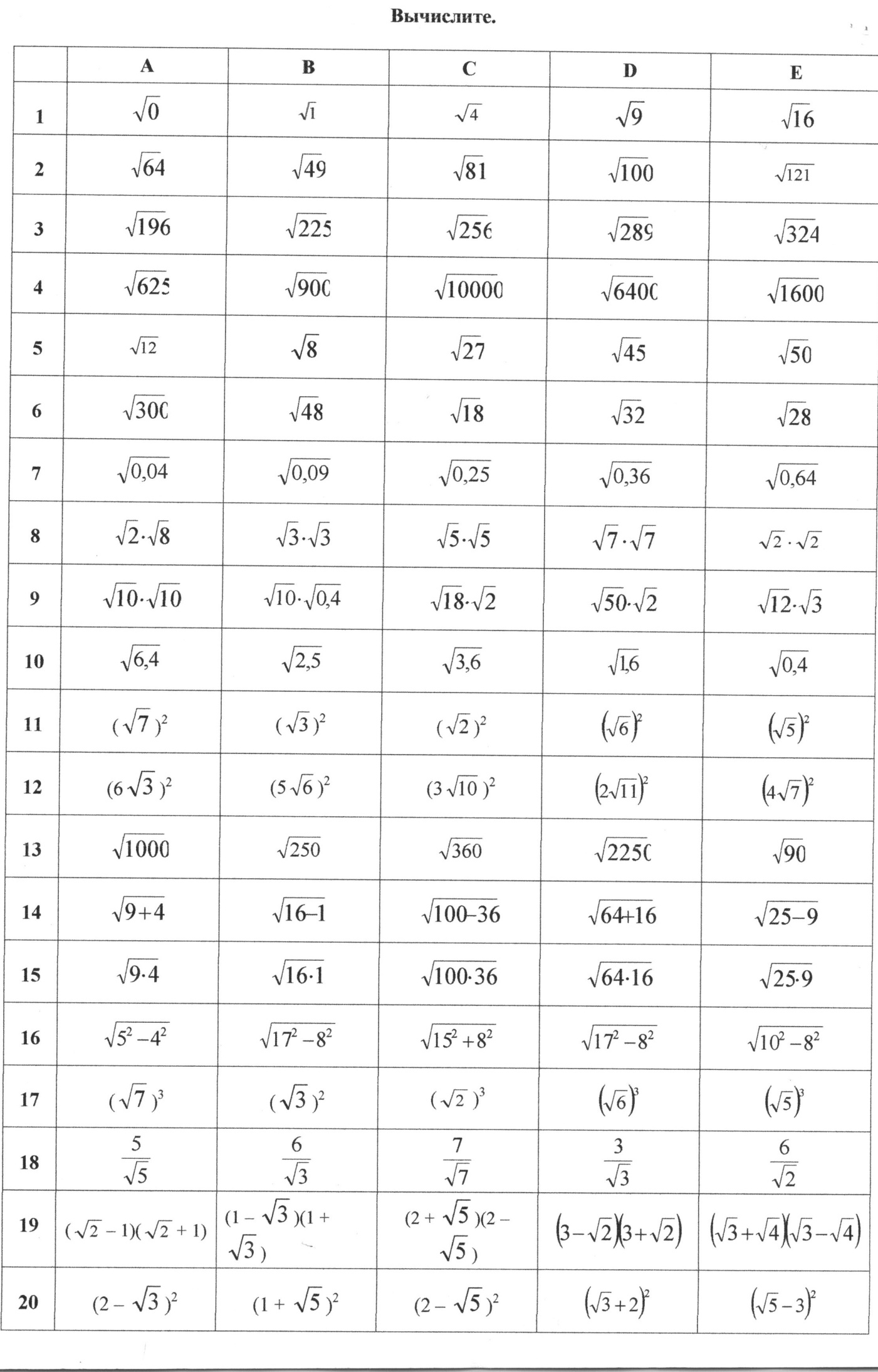
3) Устная работа по закреплению понятия арифметического корня. Приложение 1 (строки 1,2,3,4.).
Из истории. Ещё 4000 лет назад вавилонские ученые составили наряду с таблицами умножения и таблицами обратных величин (при помощи которых деление чисел сводилось к умножению) таблицы квадратов чисел и квадратных корней из чисел. При этом они умели находить приблизительное значение квадратного корня из любого целого числа. Начиная с XIII века, итальянские и другие европейские математики обозначили корень латинским словом Radix (корень) или сокращенно R. Используемый в настоящее время знак корня произошел от обозначения, которое применяли немецкие математики XV-XVI веках. Они обозначили квадратный корень точкой впереди числа или выражения. В скорописи точки заменялись черточками, позже перешедшими в символ 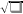 . Так, в рукописи, написанной в 1480 году на латинском языке, один такой символ точки перед числом (
. Так, в рукописи, написанной в 1480 году на латинском языке, один такой символ точки перед числом (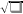 ) означал квадратный корень, два таких знака (
) означал квадратный корень, два таких знака (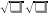 ) означали корень четвертой степени, а три знака – кубический корень. Вероятно, из этих обозначений впоследствии и образовался знак
) означали корень четвертой степени, а три знака – кубический корень. Вероятно, из этих обозначений впоследствии и образовался знак  , близкий к современному символу корня, но без верхней черты. Этот знак встречается впервые в немецкой алгебре “Быстрый и красивый счет при помощи искусных правил алгебры”, изданной в 1525 году в Страсбурге. Лишь в 1637 году Рене Декарт соединил знак корня с горизонтальной чертой.
, близкий к современному символу корня, но без верхней черты. Этот знак встречается впервые в немецкой алгебре “Быстрый и красивый счет при помощи искусных правил алгебры”, изданной в 1525 году в Страсбурге. Лишь в 1637 году Рене Декарт соединил знак корня с горизонтальной чертой.
В мире отмечается День квадратного корня – неофициальный праздник, отмечаемый девять раз в столетие в день, когда и число, и порядковый номер месяца являются квадратными корнями из двух последних цифр года. Основателем праздника является школьный учитель Рон Гордон из города Редвуд, Калифорния, США. Впервые этот праздник отмечался 09 сентября 1981 года (09.09.1981).
Вопрос: когда следующий праздник? Ответ обучающихся: 05.05.2025 г.
Закрепление
1). Решение упражнений на закрепление определения квадратного корня.
(распечатка упражнений на нахождение значений выражений, содержащих квадратные корни). Приложение 1 (строка 15, 16), приложение 2.
Итог урока.
Сформулируйте определение арифметического квадратного корня.
При каких значениях а выражение 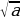 имеет смысл?
имеет смысл?
Домашнее задание.
 12 читать, учить определения; выполнить № 300, 304.
12 читать, учить определения; выполнить № 300, 304.
Список использованной литературы
1. Макарычев Ю.Н. Математика. Алгебра: 8-й класс: базовый уровень: М34 учебник / Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова; под ред. С.А.Теляковского – Москва: Просвещение, 2024 – 319 с. : ил.
2. Сиротина Т. В. Алгебра. 8 класс. Базовый уровень. Тетрадь-тренажёр / Т. В. Сиротина. — 2-е изд., эл. — 1 файл pdf : 104 с. — Москва : Издательство «Интеллект-Центр», 2024.
Приложение 1
Приложение 2
Найти значение выражения:







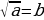 по определению.
по определению.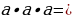
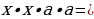
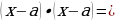
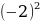 =
= 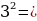
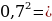
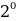 =
= 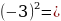
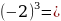
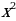 при х = 3; х = 4; х = - 5; х = 0; х =
при х = 3; х = 4; х = - 5; х = 0; х = 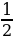 ; х = - 4 .
; х = - 4 . 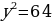 б)
б) 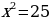 в)
в) 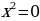

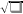 - радикал, корень.
- радикал, корень.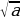 , число а при этом называют подкоренным выражением.
, число а при этом называют подкоренным выражением.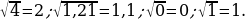
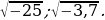
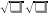 ) означали корень четвертой степени, а три знака – кубический корень. Вероятно, из этих обозначений впоследствии и образовался знак
) означали корень четвертой степени, а три знака – кубический корень. Вероятно, из этих обозначений впоследствии и образовался знак 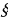 12 читать, учить определения; выполнить № 300, 304.
12 читать, учить определения; выполнить № 300, 304.











