Урок математики в 11 классе "Производная. Применение производной: Возрастание и убывание функции"

11 класс. Алгебра и начала математического анализа

Тема урока: «Применение производной: Возрастание и убывание функции».

Тип урока: урок усвоения новых знаний и первичного закрепления новых знаний.
Цель урока: Организация деятельности учащихся, направленная на овладение системой математических знаний и умений по теме «Применение производной: Возрастание и убывание функции», необходимых для решения задач ЕГЭ, применения в практической деятельности, продолжения образования.

Задачи урока:

Учебные:

- изучить понятие возрастающей и убывающей функции с использованием производной;

- сформулировать и доказать теорему Лагранжа и теорему о достаточных условиях возрастания и убывания функции;

- вывести алгоритм исследования непрерывной функции на монотонность;

- применение алгоритма на практике при решении задач;

- продолжить развивать навык по правилам дифференцирования.

Развивающие:

- развивать у учащихся умение работать самостоятельно;

- прививать интерес к математике и математическим наукам;

- развивать умение использовать научные методы познания;

- развивать память, логическое мышление, математическую речь (устную и письменную);

- способствовать развитию информационной компетенции, учебно-познавательной деятельности,

- развивать навыки использования компьютера и мультимедийных учебных программ для организации собственной познавательной и исследовательской деятельности.

Воспитательные:

- развивать усидчивость, самостоятельность, самоконтроль, наблюдательность;

- формирование опыта равноправного сотрудничества;

- содействовать формированию системы знаний.

Оборудование и материалы для урока: компьютер, интерактивная доска, интерактивная презентация для сопровождения урока, раздаточный материал.
Методы обучения: информационный (словесный), частично-поисковый
Формы организации учебной деятельности: фронтальная, индивидуальная, работа в парах.
Структура урока:
- Организационный момент.

- Актуализация знаний.
- Изучение нового материала.

- Первичное осмысление.
- Закрепление изученного материала.

- Определение домашнего задания.
- Итог урока.

Ход урока

1. Оргмомент

- Ребята, здравствуйте, садитесь!

- Сегодня у нас необычный урок. К нам пришли гости(представление гостей). Отметить отсутствующих.

- И так начнем

II. Актуализация знаний.

Сегодня для усвоения материала урока нам также необходимо вспомнить:

Фронтальный опрос: Вопросы на слайде:

1. Что называют промежутками монотонности функции

2. Какая функция называется возрастающей на промежутке?

3. Какая функция называется убывающей на промежутке?

4. Какие числовые промежутки существуют? Назовите числовые промежутки:

?

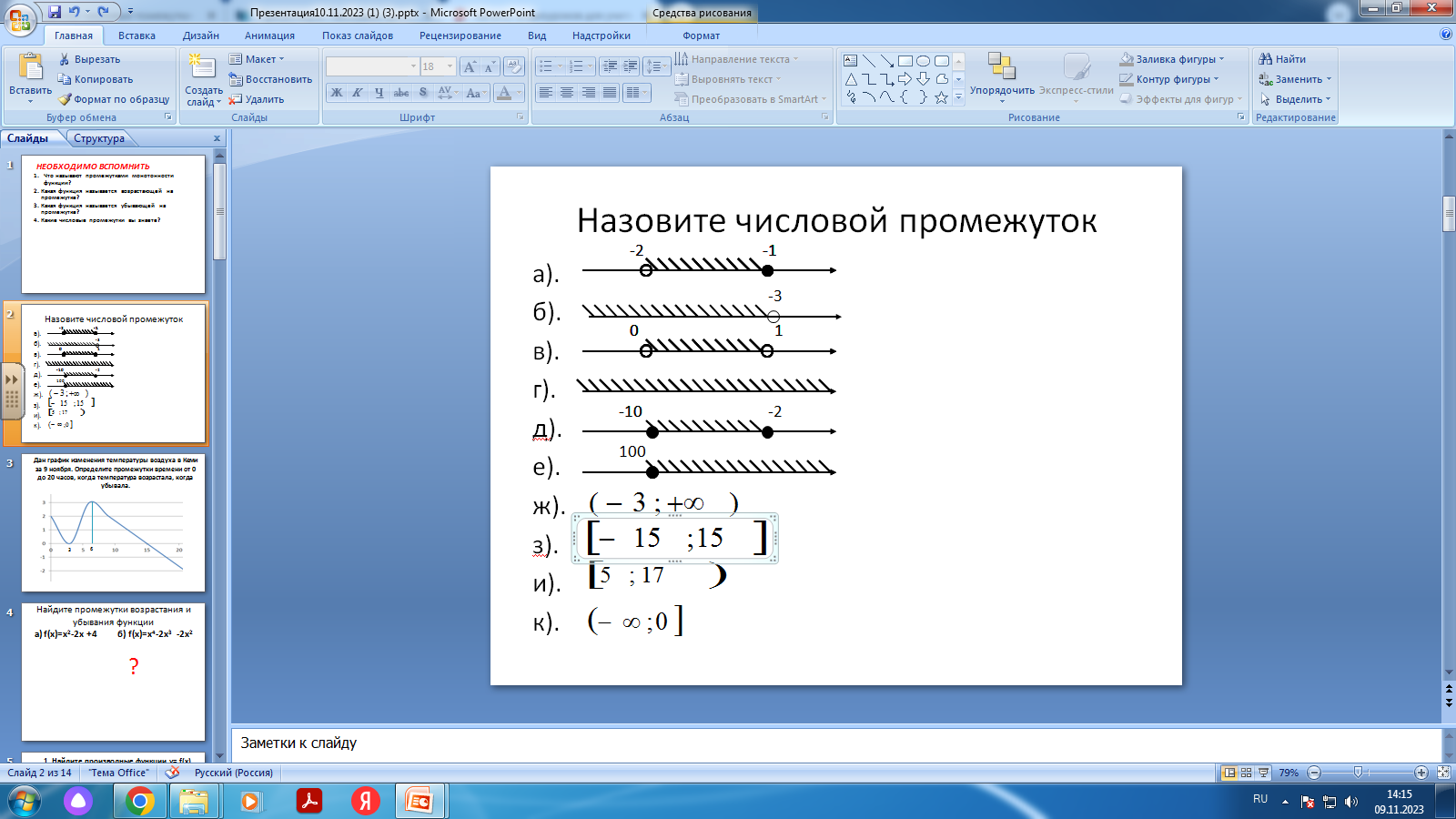5. На графике температуры воздуха в Кеми на 09 ноября найдите промежутки возрастания (убывания).

В случае, если график функции не задан, то как можно найти промежутки возрастания и убывания функции? Например, даны функции. Найдите промежутки возрастания и убывания: а) f(x)=x²-2x +4 б) f(x)=x⁴-2x³ -2x²

Для первой функции так как она является квадратичной промежутки находятся легко, во втором случае все не так просто. По результатам работы на данном этапе урока учащиеся констатируют: задание для них является невыполнимым.

- Перед нами возникает проблема . На данном этапе мы не можем ответить на эти вопросы.

-Что же делать, как нам выполнить это задание? (нам нужно разработать правило, с помощью которого мы сможем указать промежутки возрастания и убывания, возможно здесь понадобится производная.)

Производные мы вычислять умеем. Выполним задание на карточках:

Индивидуальная работа

Собираем решения и выполняем самопроверку по слайду. Если Вы верно решили задания то должно получится слово ЛАГРАНЖ.

А не является ли этот ЛАГРАНЖ тем самым ключиком для разрешения нашей проблемы. Сейчас узнаем.

(Ученик идет к доске и готовится выступить с презентацией «Теорема Лагранжа»")

Откройте тетради, запишите число и тему урока

- Какова же тема нашего урока? (изучить применение производной)

«Применение производной: Возрастание и убывание функции».

III. Изучение нового материала

а) включение в деятельность

Мы сегодня сформируем начальное представление о приложениях производной в математике и в жизни, «откроем» зависимость между свойствами монотонности функции и значениями её производной; и рассмотрим применение производной для решения задач ЕГЭ.

б) Новый материал

1. Ученик выступает с презентацией «Теорема Лагранжа». Приводит исторические сведения, доказательство теоремы Лагранжа и ее геометрический смысл.

2. Используя теорему Лагранжа мы с вами докажем теорему о достаточных условиях возрастания и убывания функции. Учитель записывает на меловой доске, делая выводы с помощью учеников. ( см.учебник Ю. М. Колягин и др. Алгебра и начала анализа стр. 107).

IV.Первичное осмысление.

1. Выполним несколько устных упражнений для закрепления сказанного.

(упражнения на слайдах).

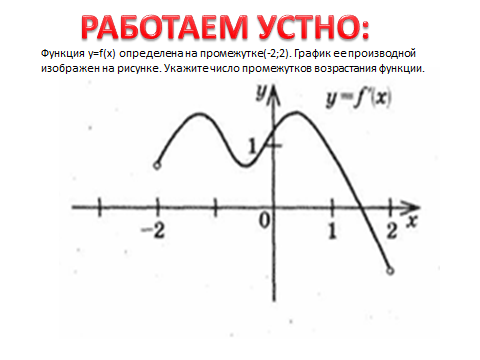
Ответ :3

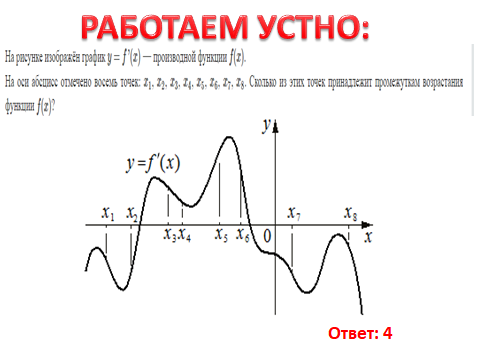
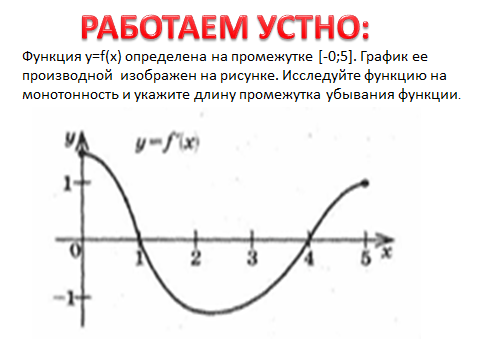
Последнее задание выполняется одним из учеников на интерактивной доске.

1. Теперь вернемся к нашей функции а) f(x)=x²-2x +4 . Не всегда удобно и возможно использовать графический способ для нахождения промежутков монотонности. Попробуем разработать алгоритм нахождения промежутков возрастания и убывания функции аналитическим путем. Определим порядок действий. Обучающиеся вместе с учителем решают задание на интерактивной доске.

2. Формулируют

Алгоритм нахождения промежутков возрастания и убывания функции

1. Найти производную исходной функции;

2. Найти нули производной и отметить их на числовой прямой;

3. Определить знак производной функции на каждом промежутке;

4. Построить таблицу и внести в нее данные о промежутках знакопостоянства производной и в соответствии со знаком производной сделать вывод возрастает или убывает функция на каждом промежутке;

5. Записать ответ.

4. Кто-нибудь из учеников находит промежутки возрастания и убывания функции f(x)=x⁴-2x³ -2x²

V. Закрепление изученного материала (работа в парах)

1. Выполнение теста из 5 заданий вар 55596890 (на сайте Решу ЕГЭ)

2.Работа с учебником: Откройте учебник на странице 109. Выполните письменно в тетради упражнения: 269(2,3,5), 270.

VI. Итог урока. Домашнее задание.

- Сегодня на уроке мы учились определять промежутки монотонности функции по графику функции и графику её производной. Сделали вывод о том, что не всегда удобно использовать графический метод для нахождения промежутков монотонности. Вывели алгоритм, при помощи которого можно находить промежутки возрастания и убывания аналитически.

- Перед вами 3 карточки. Красная, жёлтая и зелёная.

Оцените себя. Если вы считаете, что усвоили тему урока, научились находить с помощью производной точки экстремума, поднимите зелёную карточку.

Если есть небольшие затруднения, то жёлтую.Если вообще не понятно, как находить данные точки – красную.

Объявление оценок за урок.

Читать стр. 106-109, учить определения, письменно 269(4,6), 272(1).

Приложение: (карточка для индивидуальной работы).

Каждому номеру задания соответствует ответ, обозначенный буквой. Расставив буквы по порядку, Вы получите слово. Какое?