Конспект урока по математике в 5 классе СКО VIII вида.
Тема: «Обыкновенные дроби»
Цель: закрепление понятия обыкновенной дроби.
Задачи:
Закрепить понятие обыкновенной дроби, научить читать дроби, сравнивать, отличать правильные и неправильные дроби.
Развивать мыслительные процессы, зрительное восприятие, умение комментировать свои действия. Обогащать речь учащихся математическими терминами.
Воспитывать усидчивость, аккуратность, умение доводить начатое дело до конца.
Наглядность: геометрические фигуры, разделенные на равные части, карточки «Математические бусы», набор «Дроби», изготовленный учащимися на уроках технологии.
Оборудование: Компьютер, проектор, экран, презентация.
Вид урока: урок закрепления знаний.
Ход урока
Организационный момент
Получение дробей.
а) Проблемная ситуация, в которой учащиеся убеждаются в необходимости деления целого на равные части.
У ученика одно яблоко. Пришли 3 друга. Он хочет съесть яблоко вместе с друзьями. Как поступить? (ответ: Нужно разрезать яблоко на 4 равные части)
Каждому достанется 1 часть.
Что мы получили? (ответ: Мы получили дробь)
Прочитайте тему урока: «Обыкновенные дроби» (слайд 1)
Как получили дробь? (ответ: Разрезали яблоко на 4 равные части, каждому достанется одна четвертая)
Как записать?  (ответ:
(ответ: 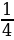 )
)
б) Понятия числителя и знаменателя дроби.
Что показывает число, которое записано под чертой дроби? (ответ: Показывает, что разделили целое на 4 равные части)
Как называется? (ответ: Называется знаменателем)
Что показывает число, которое записано над чертой дроби? (ответ: Показывает, сколько частей взяли)
Как называется? (ответ: Называется числителем)
Итак, из чего состоит дробь? (ответ: Дробь состоит из числителя и знаменателя)
в) Назовите дроби, которые вы получили в результате выполнения практической работы.
Предшествующая практическая работа:
1) деление геометрических фигур (кругов, прямоугольников, квадратов) на равные части, закрашивание нескольких частей;
2) изготовление набора «Дроби» на уроке технологии.
Какая часть у меня в руках? Что за дробь получилась?
(Учащиеся представляют свою работу, называют получившуюся дробь.)
Вывод. Мы вспомнили:
а) получение дроби; б) обозначение дроби двумя числами: числителем и знаменателем.
3. Чтение дробей учащимися (слайд 2): 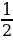 ,
, 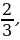
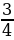 ,
, 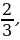
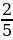 ,
, 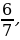
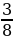 ,
, 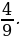
Упражнение в определении числителя и знаменателя каждой дроби. Назови знаменатель у предпоследней дроби. Назови числитель у второй дроби.
Сравнение дробей. Работа с учебником: с.118 № 475.
Запись в тетради и на доске.
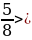
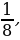
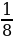

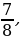
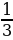

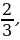
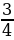

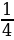 ,
, 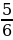

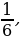
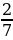

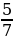 ,
, 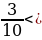
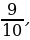
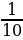

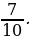
Вывод. Из дробей с одинаковым знаменателем та больше, у которой числитель больше.
Индивидуально - дифференцированная работа. Задание по карточкам: заполнить «Математические бусы» дробями в порядке возрастания, убывания.
Физ. минутка
Сколько точек будет в круге, (слайд 3)
Столько раз поднимем руки.
Сколько елочек зеленых, (слайд 4)
Столько выполним наклонов.
Приседаем столько раз, (слайд 5)
Сколько бабочек у нас.
Понятие неправильной дроби.
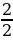 ,
, 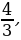
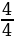 ,
, 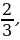
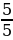 ,
, 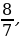
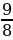 ,
, 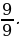 (слайд 6)
(слайд 6)
Как называются дроби, которые вы видите на экране? (ответ: Называются неправильными)
Какие дроби называются неправильными? ( ответ: У которых числитель больше знаменателя или равен знаменателю)
Упражнение на закрепление понятия неправильной дроби.
Какие числители нужно записать вместо знаков вопроса, чтобы дроби 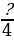 ,
,
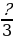 ,
, 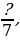
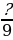 ,
, 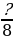 ,
, 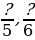 ,
, 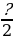 были неправильными?
были неправильными?
Работа с учебником: с. 124 № 494(3). Работа в тетради и на доске.
Вывод. У неправильной дроби числитель равен знаменателю или больше знаменателя.
Игра «Третий лишний».
Две дроби имеют общее свойство, а третья нет. Назови лишнюю дробь.
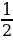 ,
, 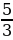 ,
, 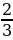 (слайд 7)
(слайд 7)
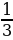 ,
, 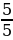 ,
, 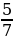 (слайд 8)
(слайд 8)
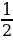 ,
, 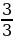 ,
, 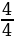 (слайд 9)
(слайд 9)
Найди дроби, которые не соответствует чертежу.
(слайды 10, 11, 12, 13) Объясни почему.
Практическое использование знаний, полученных на уроках математики. Связь с уроками технологии (отпилить 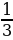 рейки), социально-бытовой ориентировки (отмерить
рейки), социально-бытовой ориентировки (отмерить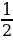 стакана муки в рецепте печенья).
стакана муки в рецепте печенья).
Оценки.
Итог. Какую тему изучали? Что понравилось на уроке? Что вызвало трудность?





 (ответ:
(ответ: 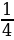 )
) 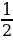 ,
, 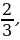
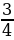 ,
, 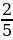 ,
, 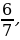
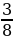 ,
, 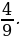
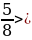
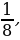
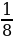

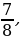
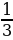
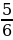
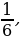
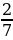
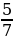 ,
, 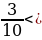
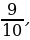
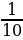
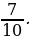
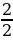 ,
, 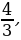
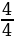 ,
, 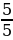 ,
, 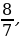
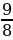 ,
, 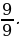 (слайд 6)
(слайд 6)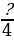 ,
,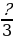 ,
, 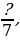
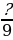 ,
, 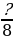 ,
, 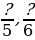 ,
, 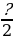 были неправильными?
были неправильными? 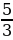 ,
, 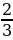 (слайд 7)
(слайд 7)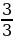 ,
, 









