Просмотр содержимого документа
«Урок на тему: Трапеция»
Урок №7 8г Дата___________
Тема урока: ТРАПЕЦИЯ
Цели урока: ввести понятия «трапеция»; рассмотреть решение задач, в которых раскрываются свойства трапеции.
Развивающие: развивать логическое мышление учащихся.
воспитательная – воспитание трудолюбия, взаимопомощи, математической культуры; воспитание чувства ответственности перед товарищами, умение контролировать свои действия.
Планируемые результаты:
Личностного развития:
продолжать развивать умение ясно, точно и грамотно излагать свои мысли в устной и письменной речи,
развивать креативность мышления, инициативу, находчивость, активность при решении математических задач.
Метапредметного развития:
расширять кругозор, прививать умение совместно работать (чувство товарищества и ответственности за результаты своего труда);
продолжать развивать умение понимать и использовать математические средства наглядности.
Предметного развития:
формировать умение применять изученные понятия для решения задач практического характера.
Тип урока: комбинированный
Оборудование: учебник, доска, мел
Ход урока
Организационный момент
Изучение нового материала.
1. Вспомнить с учащимися определение параллелограмма.
2. Трапеция - четырехугольник, у которого две противолежащие стороны параллельны, а две другие – непараллельны.
Рассмотрим четырехугольник, про который можем сказать , что две противолежащие стороны параллельны, две другие не параллельны.
Трапеция – (от греч. trapezion, букв. – столик).
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные.
Виды трапеции. Равнобедренная – трапеция, у которой равны боковые стороны.
Прямоугольная – трапеция, один из углов которой прямой.
III. Решение задач.
№ 385 (решена в учебнике), № 386 (по теореме Фалеса). Можно после решения этой задачи дать определение средней линии трапеции.
IV. Итоги урока.
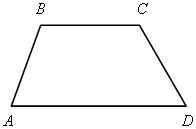
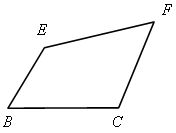
1. АВСD, ВЕFC – трапеции.
2. Частные виды трапеции:
| 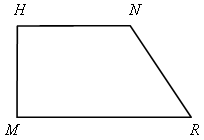
Прямоугольная трапеция | 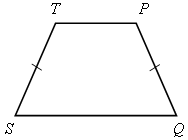
Равнобокая трапеция
(равнобедренная) |
| 3. В решении задач на трапецию можно использовать свойства углов при параллельных прямых и секущей 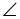 1 = 1 = 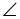 2 (как внутренние накрест лежащие при ВС || АD и секущей ВD). 2 (как внутренние накрест лежащие при ВС || АD и секущей ВD). | 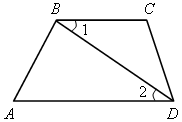
|
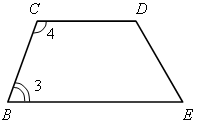
| 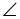 3 + 3 + 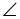 4 = 180° (как внутренние односторонние при СD || ВЕ и секущей ВС). 4 = 180° (как внутренние односторонние при СD || ВЕ и секущей ВС).
| 
|
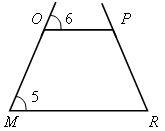
| 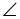 5 + 5 + 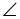 6 (как соответственные при ОР || MR и секущей ОМ). 6 (как соответственные при ОР || MR и секущей ОМ).
| 
|
4. Применение теоремы Фалеса в трапеции:
| а) ВС || MN || KР || QS || АD и МВ = МK = KQ = QA, то CN = NP = PS = SD; б) МВ = МK = KQ = QA и CN = NP = PS = SD, то ВС || MN || KP || QS || AD. | 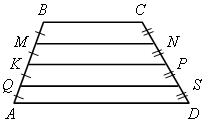
|
Домашнее задание: вопросы 10, 11, с. 114; № 384, № 387.



























