Урок по алгебре в 11 классе "Решение уравнений"

ОБОБЩАЮЩИЙ УРОК ПО АЛГЕБРЕ В 11 КЛАССЕ

«РЕШЕНИЕ УРАВНЕНИЙ»

УМК: А.Г. Мордкович, Алгебра и начала анализа. 10-11 классы

Тип урока: Комплексное применение знаний.

Цели урока:

Образовательные: обобщение и систематизация, расширение и углубление знаний по теме «Квадратные уравнения»; выработка умений самостоятельно применять знания, осуществлять их перенос в новые условия; повышение качества знаний школьников.

Развивающие: активизировать познавательную деятельность школьников; способствовать развитию алгоритмического мышления учащихся; расширить представления учащихся о сферах применения математики, развивать интеллектуальные качества личности школьников такие, как самостоятельность, способность к оценочным действиям, обобщению, быстрому переключению; способствовать формированию навыков самостоятельной работы; формировать умения четко и ясно излагать свои мысли.

Воспитательные: расширить сферу математических знаний, общекультурный кругозор учащихся; формировать умения аккуратно и грамотно выполнять записи.

Основные этапы урока:

1) подготовительный этап – мотивация необходимости изучения учебного материала;
2) обучающий этап – работа с алгоритмом решения квадратного уравнения;
3) самоконтроль при подготовке к выполнению самостоятельной работы;
4) самостоятельная работа.

Для осуществления поставленных на урок задач выбраны следующие методы и формы обучения:

методы: формы:

наглядный; общеклассная;

практический; индивидуальная;

словесный;

частично-поисковый.

Ход урока:

I. Орг. момент.

II. Актуализация опорных знаний.

Слайд 2.

1) Историческая справка. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н.э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.

Древнеиндийский математик Баудхаяма в VIII столетии до н.э. впервые использовал квадратные уравнения в форме ax² = c и ax² + bx = c и привел методы их решения.

Вавилонские математики примерно с IV века до н.э. и китайские математики примерно со II века до н.э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения.

Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был Брахмагупта (Индия, VII столетие нашей эры).

Слайд 3.

2) При каком условии квадратное уравнение не имеет корней?

3) Чему равно произведение и сумма корней приведенного квадратного уравнения?

4) Для каких квадратных уравнений, не решая их, можно сказать, что они имеют два различных корня?

III. Систематизация знаний.

Рассмотреть задания ЕГЭ, приводящие к решению квадратных уравнений.

Слайд 4.

Задание В14.

Найдите наибольшее значение функции f(x) = x³ – 5x² + 7x – 6 на отрезке [0; 2].

Решение: f(x) = 0,

3x² – 10x + 7 = 0,

D/4 = 25 – 21 = 4, D/4 0,

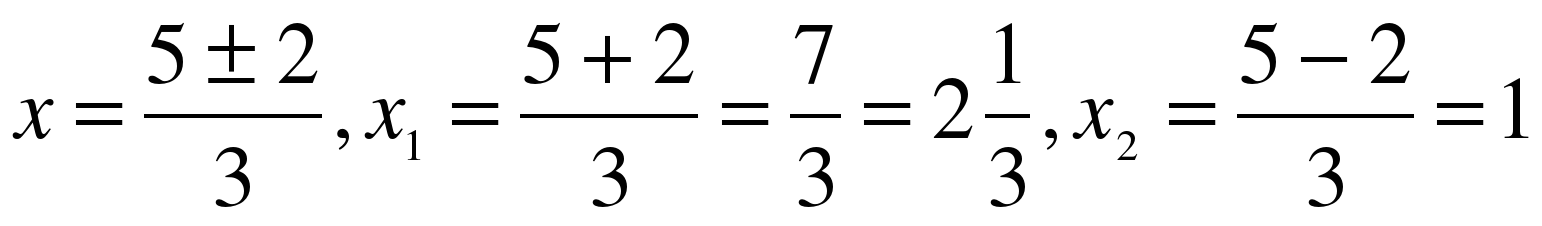
f(0) = - 6,

f(1) = - 3,

f(2) = - 4.

Ответ: - 3.

Слайд 5.

Задание В13.

Катер в 10.00 вышел из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 15 мин., катер отправился назад и вернулся в пункт А в 14.00 того же дня. Определите (в км/ч) собственную скорость катера, если известно, что скорость течения реки равна 1 км/ч.

Решение:

Слайд 6.

Пусть скорость катера х км/ч.

v t S

По течению (x + 1) км/ч ч 15 км

Против течения (x – 1) км/ч ч 15 км

Время в пути: 2 ч 45 мин = ч

Составим и решим уравнение:

Ответ: 11 км/ч.

Слайд 7.

Задание С1.

1. Решите систему уравнений:

Решение:

Решим первое уравнение системы.

Пусть sinx = t, тогда

2t² – 3t + 1 = 0,

D = 9 – 8 = 1, D 0,

sin x = 1, sin x = ,

x₁ = x₂ =

x₃ =

Из второго уравнения системы имеем: y = cos x.

Подставим найденные значения в данное уравнение:

- не удовлетворяет условию y 0,

- удовлетворяет условию y 0,

- не удовлетворяет условию y 0.

Ответ:

Слайд 8.

1. Решите систему уравнений:

Решение:

Решим первое уравнение системы, пусть 4^{sin y} = t, t 0.

2t² + 3t – 2 = 0,

D = 9 + 16 = 25, D 0,

Уравнение решений не имеет.

Подставим найденные значения во второе уравнение системы:

Уравнение решений не имеет.

Ответ: (1;

Слайд 9.

Задание С5.

1) Найдите все значения параметра а, при каждом из которых уравнение

x² -(|a + 5| − |a - 5|)x + (a - 12)(a + 12) = 0

имеет два различных отрицательных корня.

Решение:

Используя теорему Виета, запишем условия существования двух различных отрицательных корней для квадратного уравнения:

x₁x₂ 0

x₁ + x₂ 0