Урок по геометрии "Призма. Поверхность призмы"

Подготовила :

Якубова А.Р.,

учитель математики первой квалификационной категории

• Понятие и чертёж
• Элементы призмы
• Общие свойства призм
• Виды призм и их особенности
• Поверхность призм
• Сечения призм
• Призмы вокруг нас

• Чертёж призмы

• Призма -

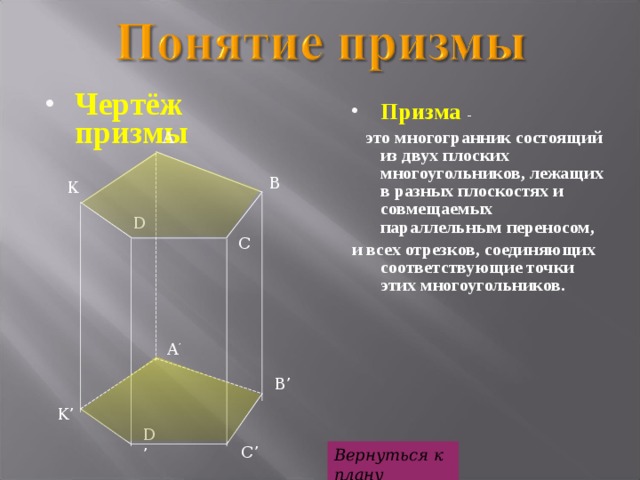
это многогранник состоящий из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом,

и всех отрезков, соединяющих соответствующие точки этих многоугольников.

А

В

К

D

С

A ’

B’

K’

D’

C’

Вернуться к плану

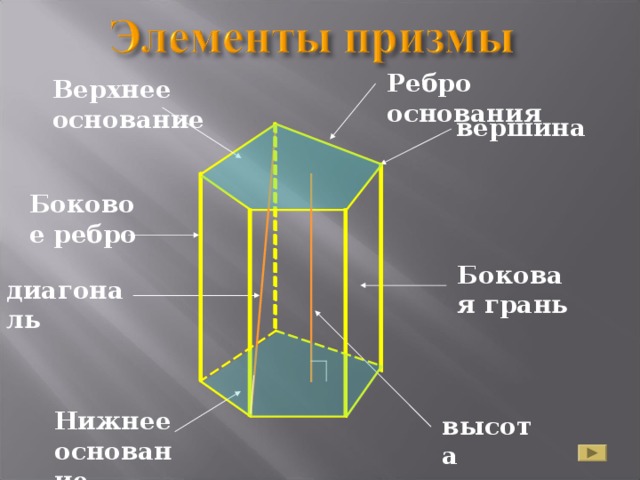
Ребро основания

Верхнее основание

вершина

Боковое ребро

Боковая грань

диагональ

Нижнее основание

высота

• Основания –

это грани, совмещаемые параллельным переносом.

• Боковая грань –

это грань, не являющаяся основанием.

• Боковые рёбра –

это отрезки, соединяющие соответствующие вершины оснований.

• Вершины –

это точки, являющиеся вершинами оснований.

• Высота –

это перпендикуляр, опущенный из одного основания на другое.

• Диагональ –

это отрезок, соединяющий две вершины, не лежащие в одной грани.

Вернуться к плану

• Основания призмы равны
• Основания призмы лежат в параллельных плоскостях
• У призмы боковые рёбра параллельны и равны
• Любая боковая грань является параллелограммом

Вернуться к плану

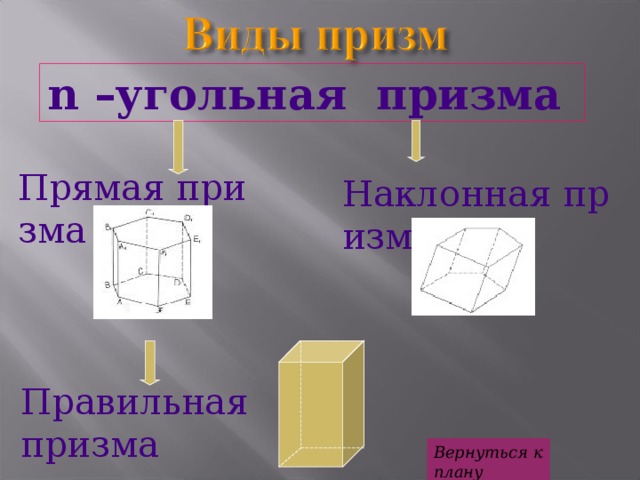
n – угольная призма

Прямая призма

Наклонная призма

Правильная призма

Вернуться к плану

• - это призма, в основании которой лежит n - угольник

Треугольная призма

Шестиугольная призма

Четырёхугольная призма

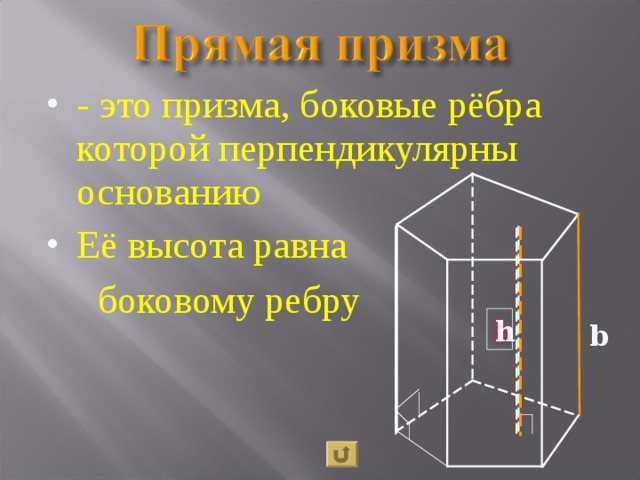
• - это призма, боковые рёбра которой перпендикулярны основанию
• Её высота равна

боковому ребру

h

h

b

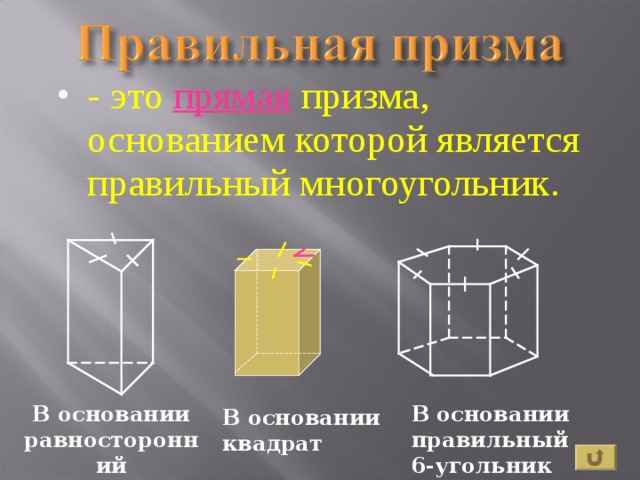
• - это прямая призма, основанием которой является правильный многоугольник.

В основании равносторонний треугольник

В основании правильный

6-угольник

В основании квадрат

• - это призма, боковые рёбра которой не перпендикулярны основанию.

h

Полная поверхность

S полн.

Поверхность – это сумма

площадей граней

Поверхность оснований S осн

Боковая поверхность S бок

+

• Теорема:

Боковая поверхность прямой призмы равна произведению периметра основания на длину бокового ребра.

Дано: прямая n- угольная призма, a 1 , а 2 … а n - стороны основания, l - боковое ребро.

Доказать: S бок = P осн l

Вернуться к плану

• Боковые грани прямой призмы – прямоугольники у которых сторонами являются стороны основания призмы и боковые рёбра призмы S 1 = a 1 l , S 2 =a 2 l …S n = a n l
• S бок = S 1 +S 2 +…S n = a 1 l + a 2 l + a n l =

(a 1 +a 2 +…a n ) l =P осн l

Теорема доказана

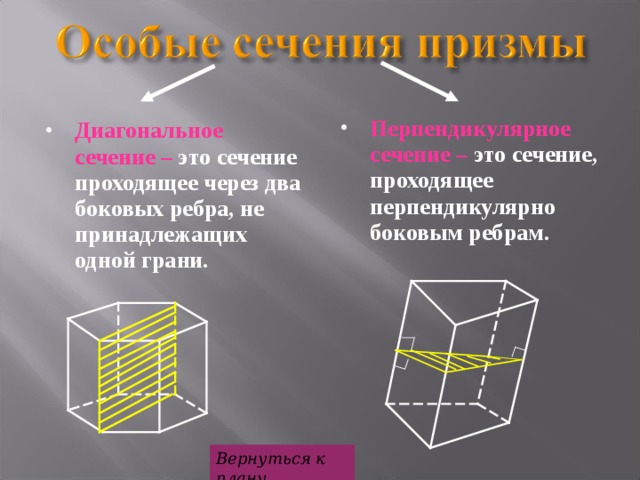
• Перпендикулярное сечение – это сечение, проходящее перпендикулярно боковым ребрам.

• Диагональное сечение – это сечение проходящее через два боковых ребра, не принадлежащих одной грани.

Вернуться к плану