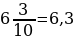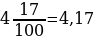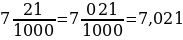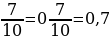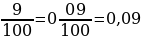Урок по математике "Десятичная дробь" 6 класс

ОК -6 Десятичные дроби

Десятичная дробь –это число, в записи которого целая часть отделена от дробной части запятой.

дробная часть (числитель)

а, . . . . .

десятые

сотые

тысячные

десятитысячные

и т. д.

Десятичная дробь получена из числа, знаменатель дробной части которого равен 10;100;1000 и т. д.

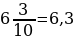
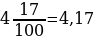
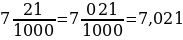
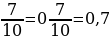
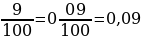
Сравнение десятичных дробей

1. Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь, равная данной.

6 дм = 0,6 м 6 дм = 60 см = 600 мм, значит

60 см = 0,60 м 0,6 = 0,60 = 0,600…

600 мм = 0,600 м

1. При сравнении десятичных дробей с одинаковой целой частью надо:

а) уравнять количество знаков после запятой;

б) сравнить дроби не обращая внимания на запятую.

Пример. Сравнить дроби 5,345 и 5,36.

5,345 ˂ 5,360, значит 5,345 ˂ 5,36.

1. Если целые части дробей не равны, то большей будет та дробь, целая часть которой больше.

Пример. Сравнить дроби 8,5 ˃ 4,543.

1. Сравнить десятичные дроби можно поразрядно 2,681 ˂ 2,69, т. к.

8 ˂ 9

Изображение десятичных дробей на координатном луче

Меньшая десятичная дробь лежит на координатном луче левее большей, и большая – правее меньшей.

Равные десятичные дроби изображаются одной и той же точкой.

Сложение и вычитание десятичных дробей

Чтобы сложить (вычесть) десятичные дроби, нужно:

1. уравнять в этих дробях количество знаков после запятой;

2. записать их друг под другом, чтобы запятая была записана под запятой;

3. выполнить сложение (вычитание), не обращая внимания на запятую;

4. поставить в ответе запятую под запятой в данных дробях.

3, 7 + 2,651 = 3 ,700 3,7 – 2,651 = 3, 700 145 – 78,65 = 145, 00

+ 2 ,651 - 2, 651 - 78,65

6 ,351 1,049 66,35

Округление чисел

1. Округление числа до целого – замена числа ближайшим к нему натуральным числом или нулем.

Пример. Округлить 3, 142 и 3,903 до целого.

Число 3, 142 ближе к 3, значит 3,142 ≈ 3;

число 3,903 ближе к 4, значит 3,903 ≈ 4.

1. Округление числа до какого – нибудь разряда: все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают.

Если после округляемого разряда стоят цифры 0;1;2;3;4, то округляемую цифру не изменяют, а последующие за ней отбрасывают. Если после округляемого разряда стоят цифры 5;6;7;8;9, то округляемую цифру увеличивают на 1.

Пример. Округлить 86, 2753 до:

а) десятых 86, 2753 ≈ 86,3 в) тысячных 86, 2753 ≈ 86,275

б) сотых 86, 2753 ≈ 86,28 г) десятков 86, 2753 ≈ 90