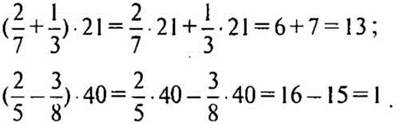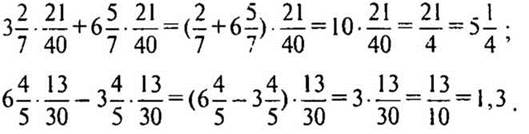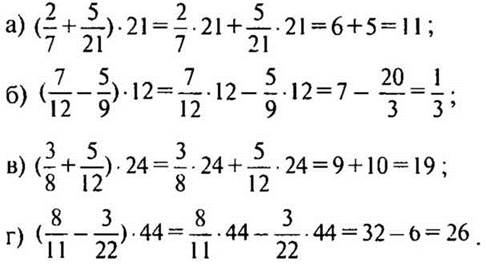Урок по теме «Применение распределительного свойства умножения», 6 класс

Урок по теме «Применение распределительного свойства умножения», 6 класс

Цели: повторить распределительное свойство умножения относительно сложения и вычитания; способствовать формированию и развитию логического мышления, умению формулировать и обосновывать суждения; воспитывать аккуратность, точность и внимательность при работе с дробями.

Ход урока

I. Организационный момент

«Незнанием никогда не следует хвалиться: незнание есть бессилие». (Н. Г. Чернышевский)

II. Анализ самостоятельной работы

1. Познакомить учащихся с результатами самостоятельной работы.

2. Решить задания, в которых допущено наибольшее количество ошибок.

III. Устный счет

1. № № учебника

2. Сумма каких двух натуральных чисел равна их произведению?

(Ответ: 2 + 2 = 4; 2 · 2 = 4.)

3. С помощью приема прикидки определите:

21% от 1990 руб. (400 руб.)

76% от 4012 км (3000 км)

9% от 200 г (20 г)

4. Из 6 спичек сделайте 4 равных равносторонних треугольника. (Треугольная пирамида.)

IV. Сообщение темы урока

— На уроке мы будем рассматривать, в каких случаях удобнее применять распределительное свойство умножения. Помните, что всегда нужно смотреть, как удобнее выполнить вычисления.

V. Изучение нового материала

1. Подготовительная работа. Фронтальный опрос.

1) Как умножить дробь на натуральное число?

2) Как найти дробь от числа?

3) Что такое 1%?

4) Как найти несколько процентов от числа?

5) Что значит сократить дробь?

6) Записать и сформулировать распределительный закон умножения относительно сложения и относительно вычитания.

7) Какие преобразования выражений позволяет выполнять распределительный закон?

2. Работа над новой темой.

— Рассмотрим случаи, когда применение распределительного свойства умножения помогает упрощать вычисления.

1) Найдите значение выражения:

Решение:

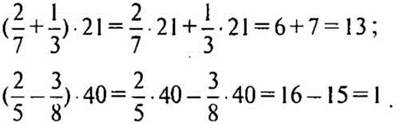
(Ответ: а) 13; б) 1.)

— Запишем распределительное свойство умножения в следующем виде:

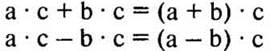
— Подтвердите это примерами.

2) Найдите значение выражения:

Решение:

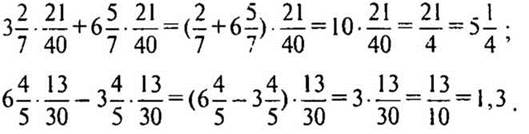
(Ответ:  )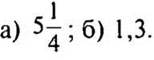

VI. Закрепление изученного материала

№ 536 стр. 88 (с подробным комментированием у доски и в тетрадях).

Решение:

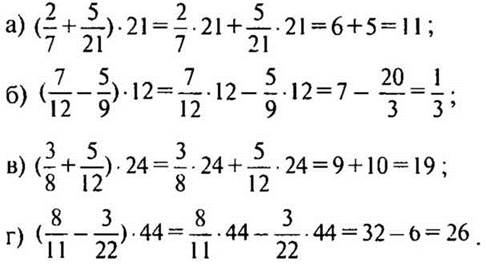
(Ответ: а) 11; б) 1/3; в) 19; г) 26.)

VII. Физкультминутка

VIII. Работа над задачей

— Решите задачу. От куска проволоки отрезали сначала 40%, а потом еще 30% остатка. Сколько процентов куска проволоки осталось?

Решение:

Пусть 100% — весь кусок проволоки.

100 — 40 = 60% — осталось после того, как отрезали 40%.

60% = 0,6

30% = 0,3

0,6 · 0,3 = 0,18 = 18% — отрезали во второй раз.

60 - 18 = 42% — проволоки осталось.

(Ответ: 42%.)

IX. Повторение изученного материала

№ 554 стр. 90 (на обратной стороне доски, самопроверка).

— Как найти куб числа?

— Как умножить дробь на дробь?

(Ответ:  )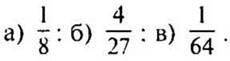

X. Самостоятельная работа

№№ учебника

XI. Подведение итогов урока

— Сформулируйте распределительное свойство умножения относительно сложения и вычитания.

— Расскажите, как упростить выражение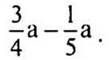 

Выставление оценок.

Домашнее задание