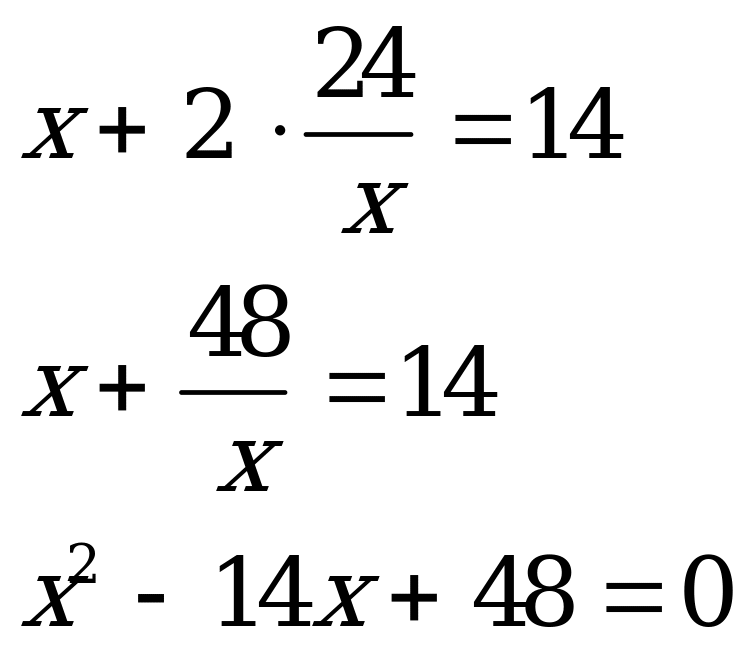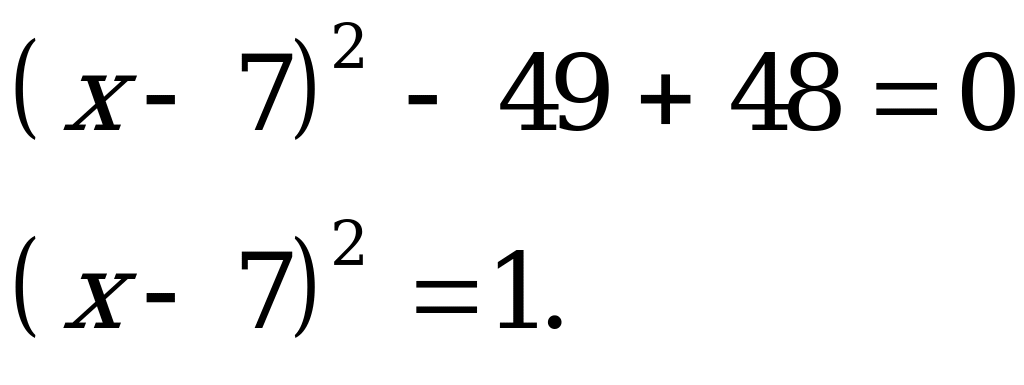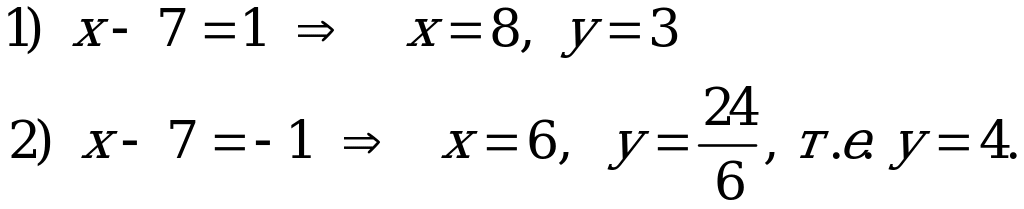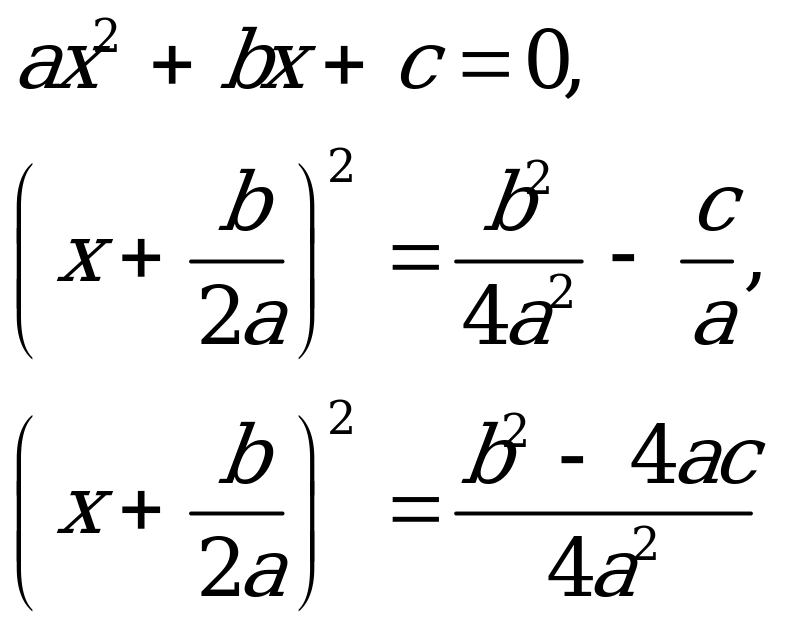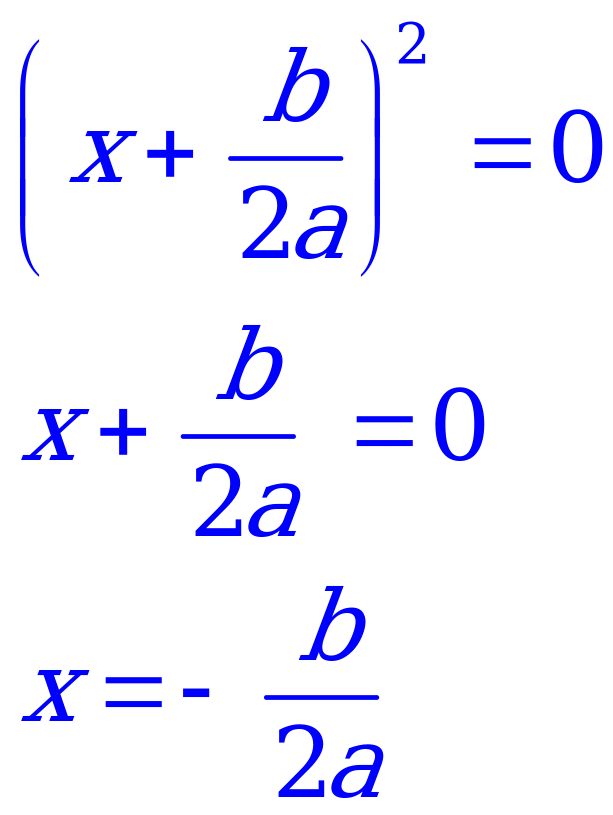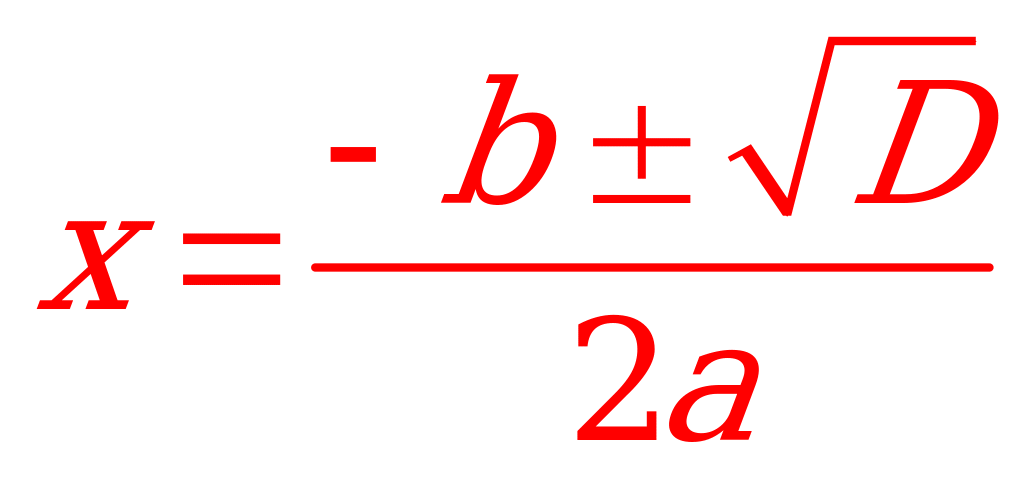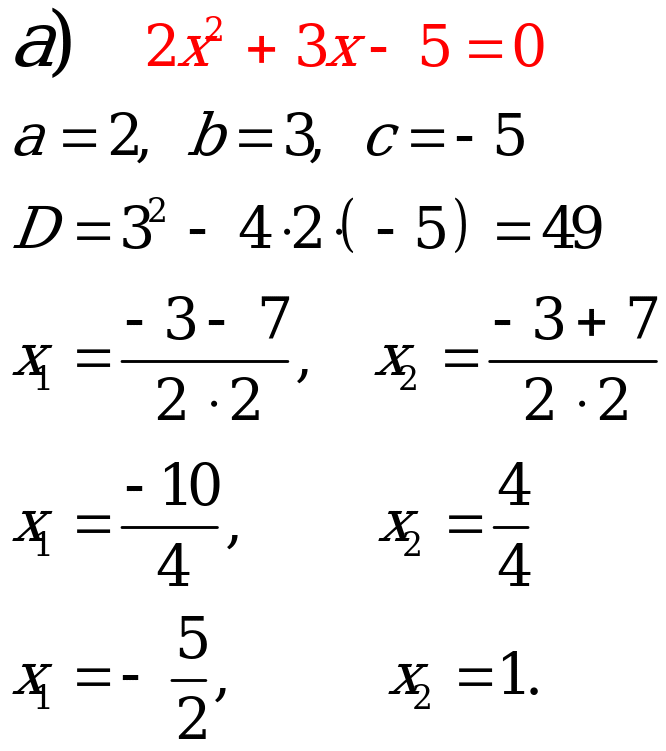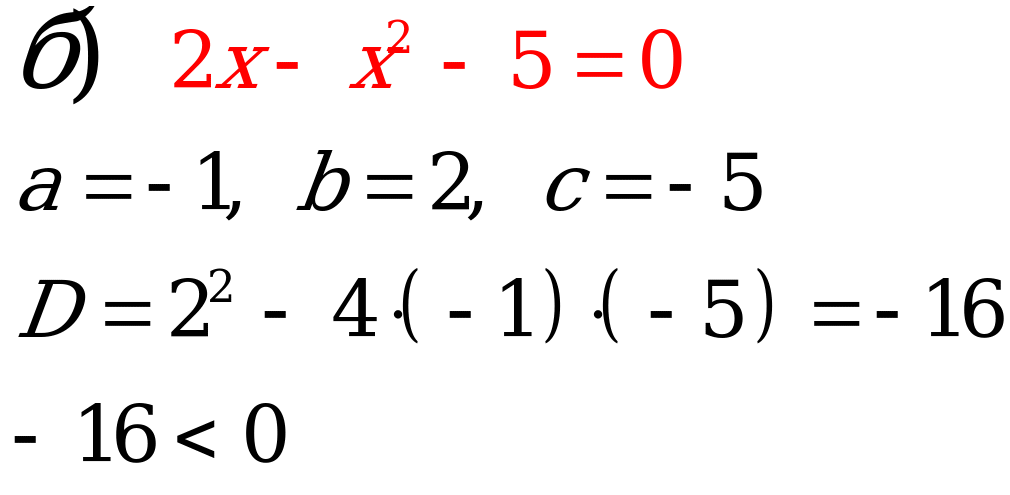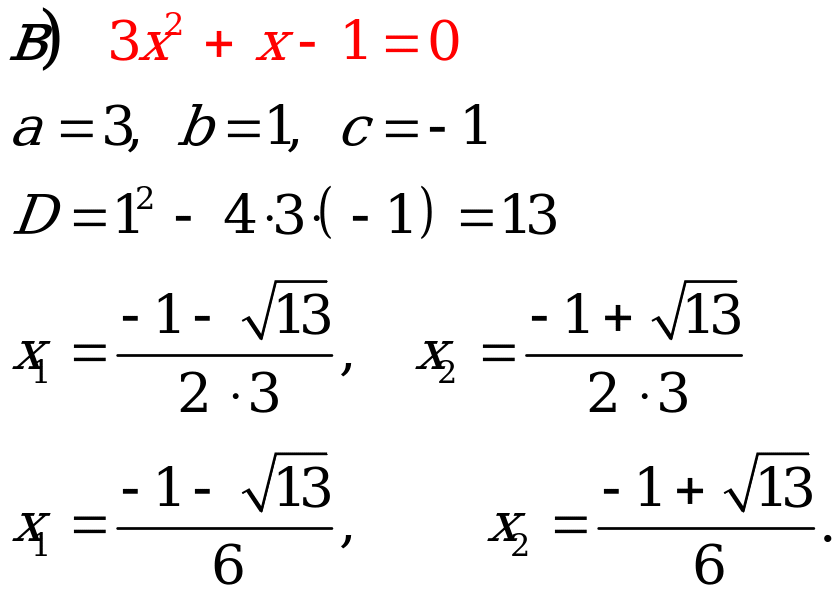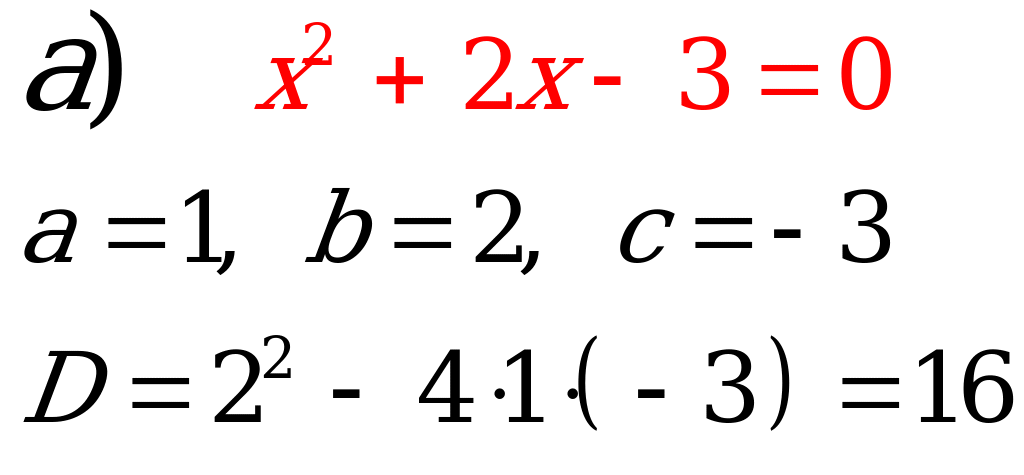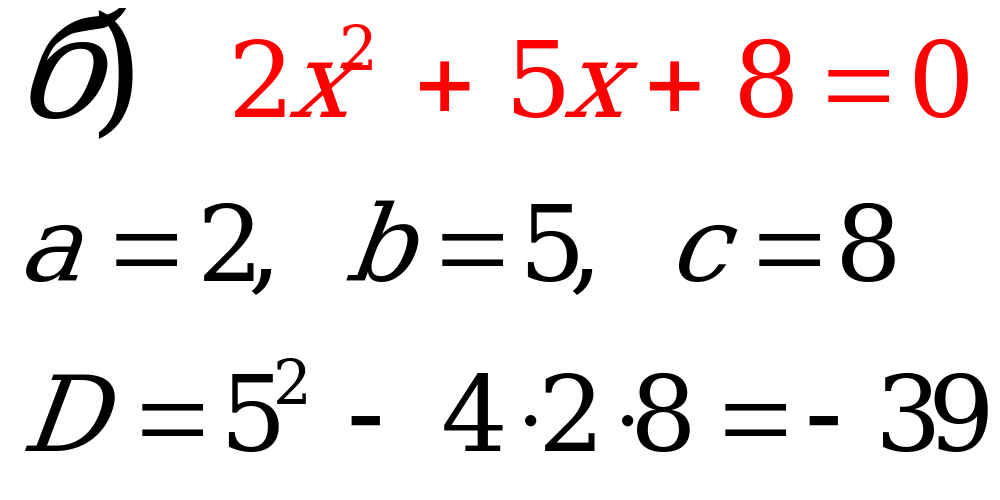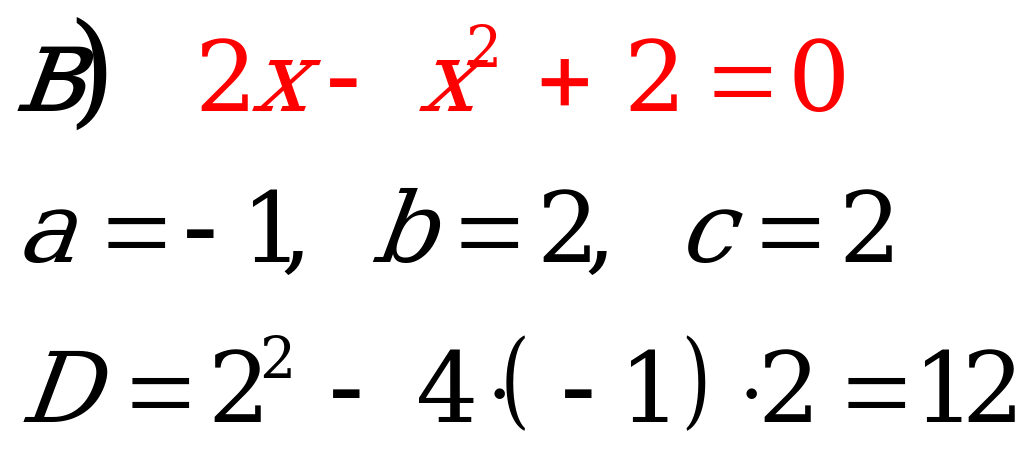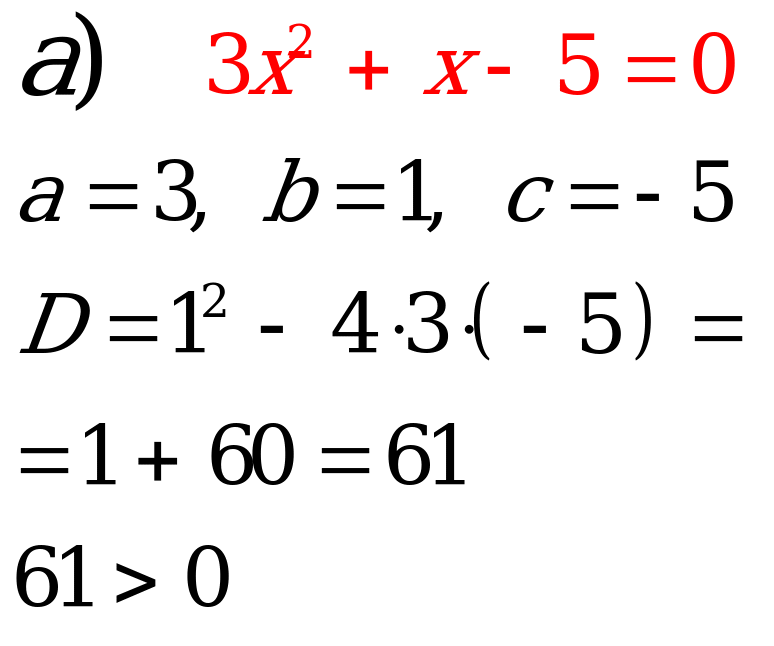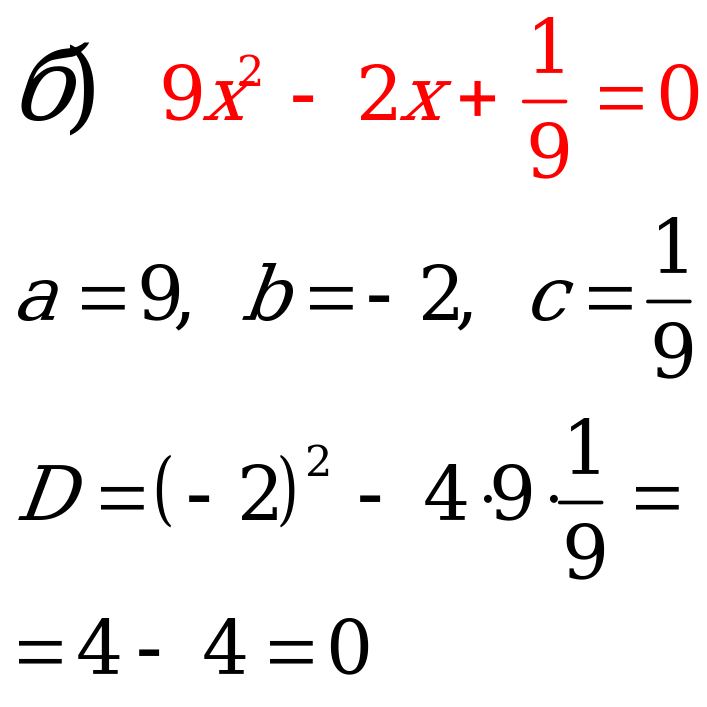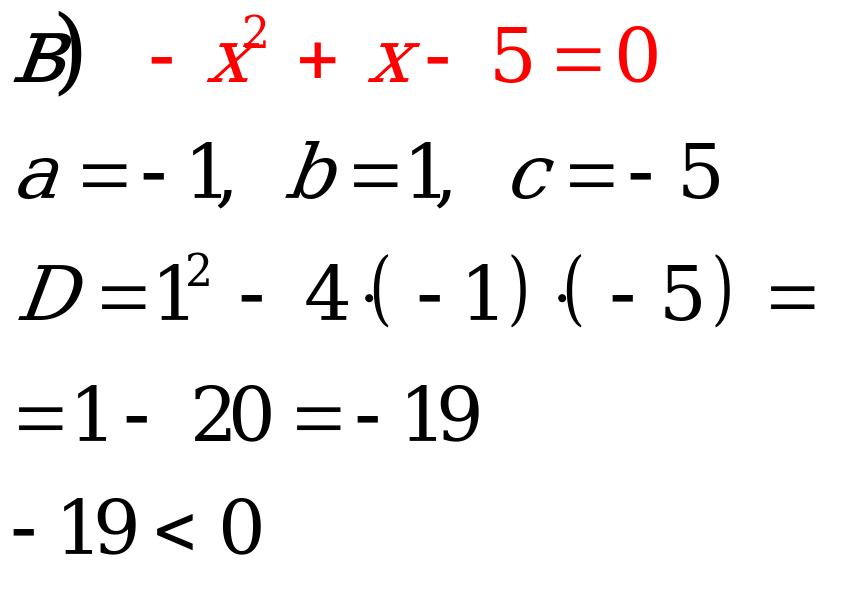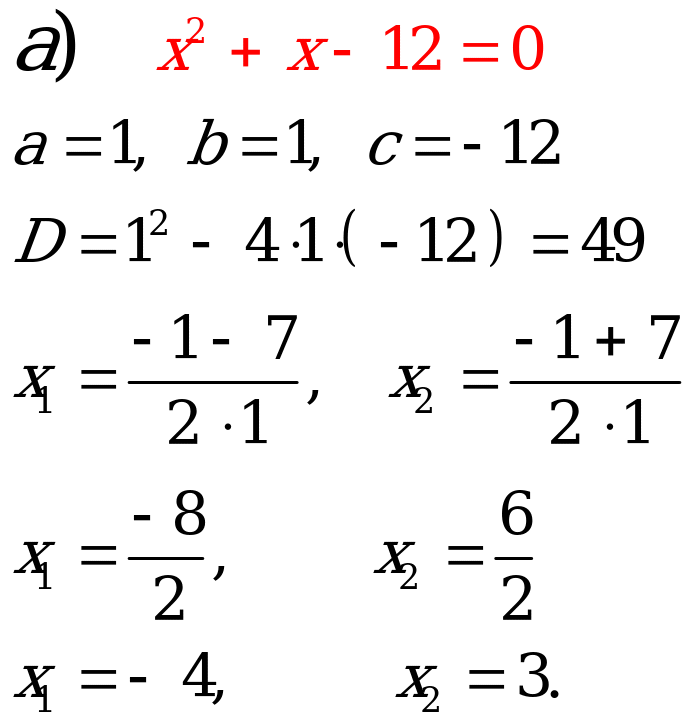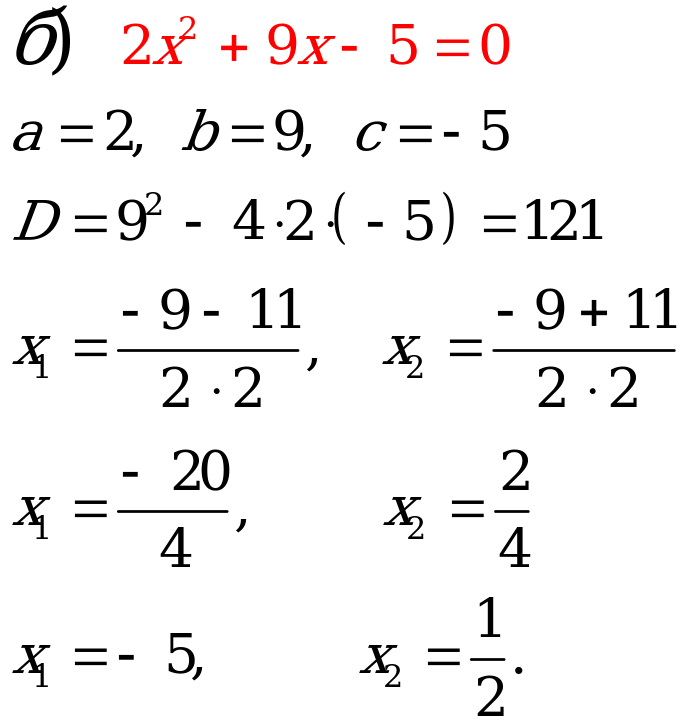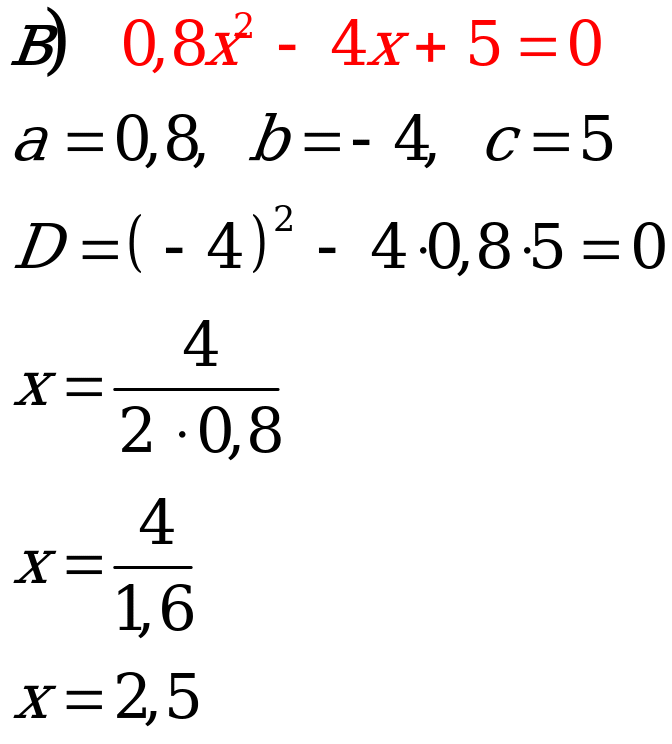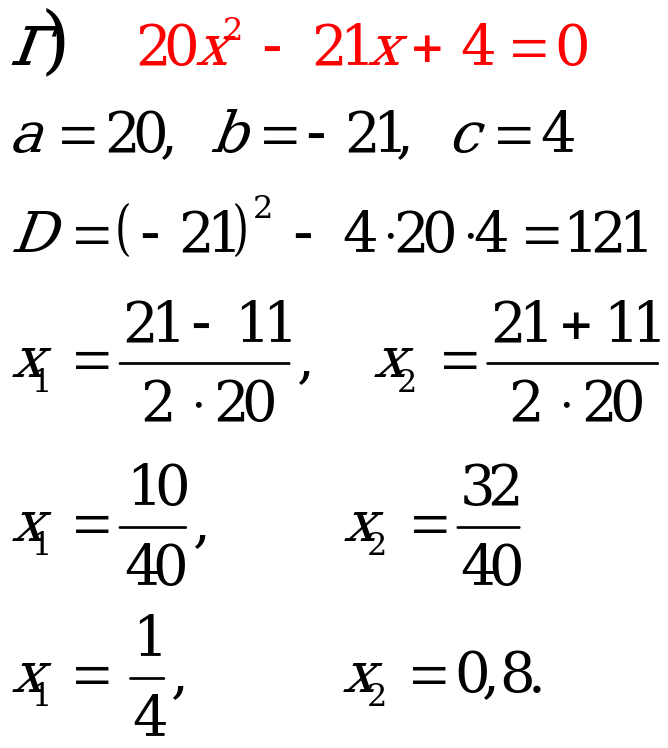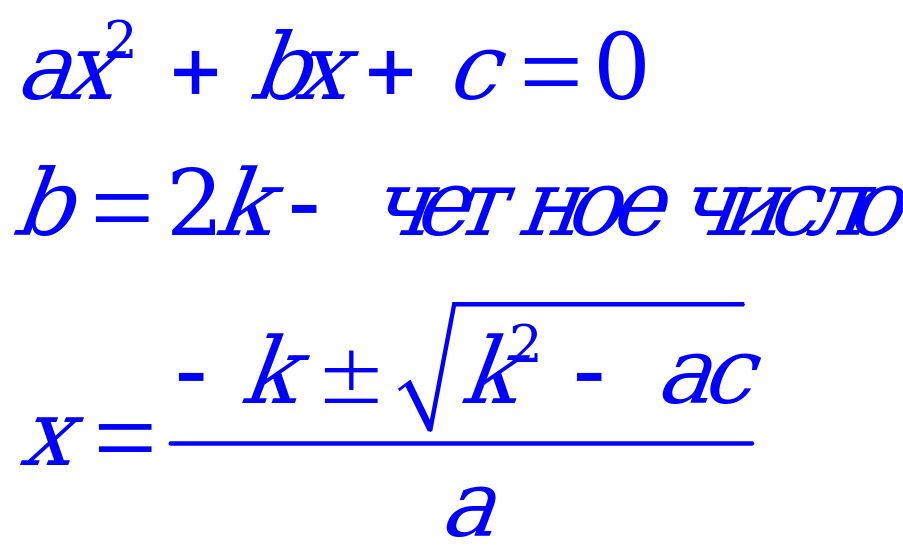Тема: «Формулы для решения квадратных уравнений»
Цель урока:
Ход урока:
Слово учителя.
Впервые квадратное уравнение сумели решить математики Древнего Египта. В одном их математических папирусов содержится задача: «Найти стороны поля, имеющего форму прямоугольника, если его площадь 12, а 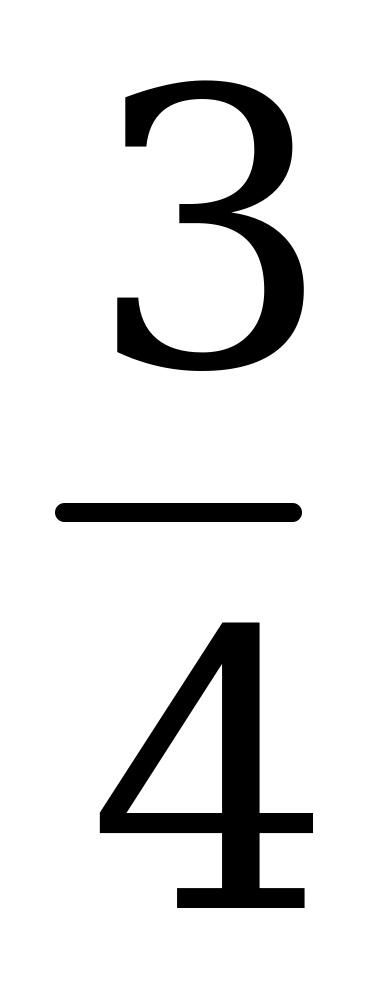 длины равны ширине». Рассмотрим её.
длины равны ширине». Рассмотрим её.
Пусть 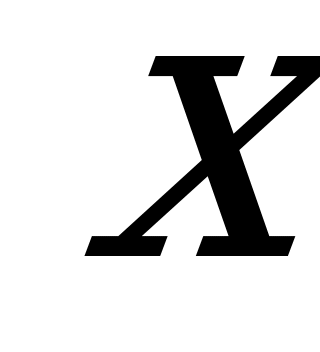 - длина поля. Тогда
- длина поля. Тогда 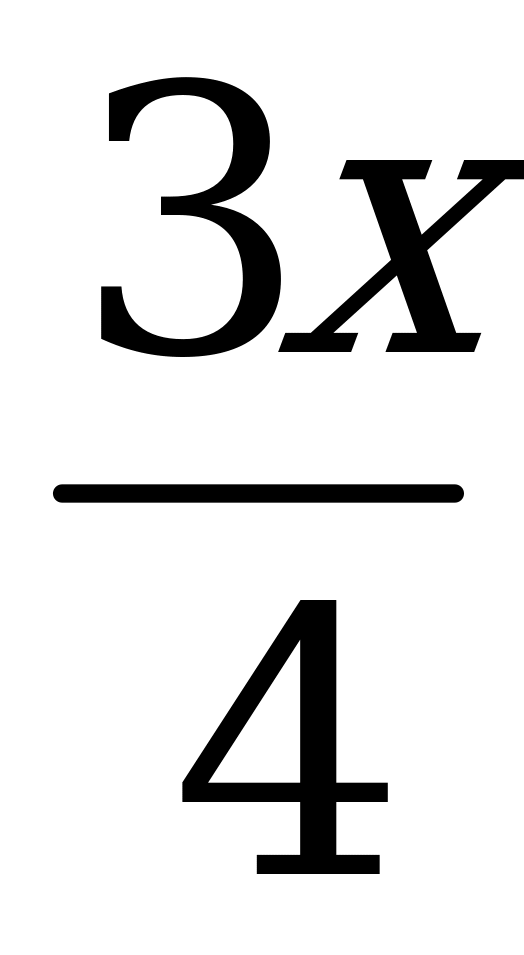 - его ширина,
- его ширина,  - площадь. Получилось квадратное уравнение:
- площадь. Получилось квадратное уравнение: 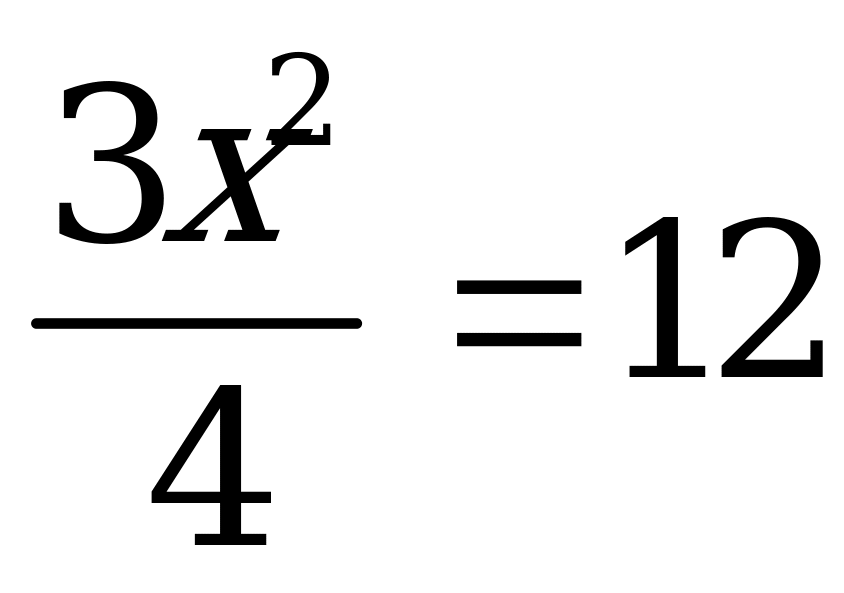 . В папирусе дано правило для его решения: «Раздели 12 на
. В папирусе дано правило для его решения: «Раздели 12 на 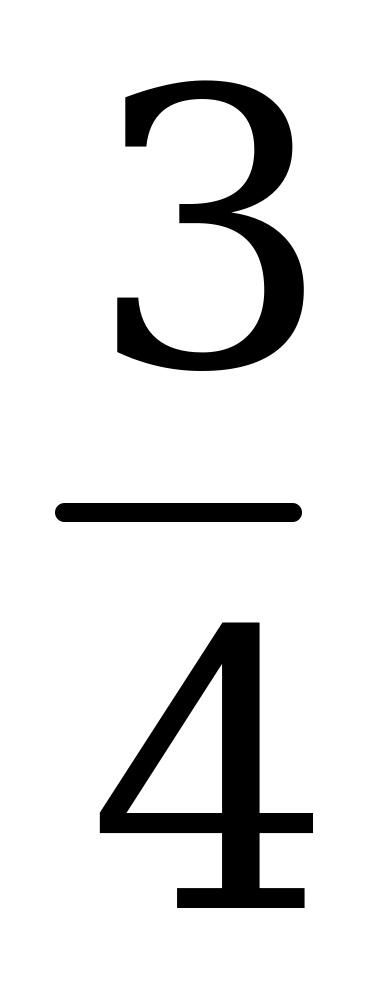 ».
».
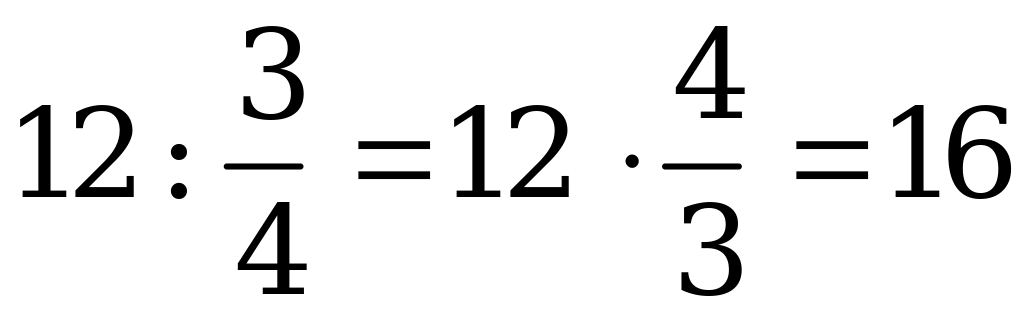 .
.
Итак, 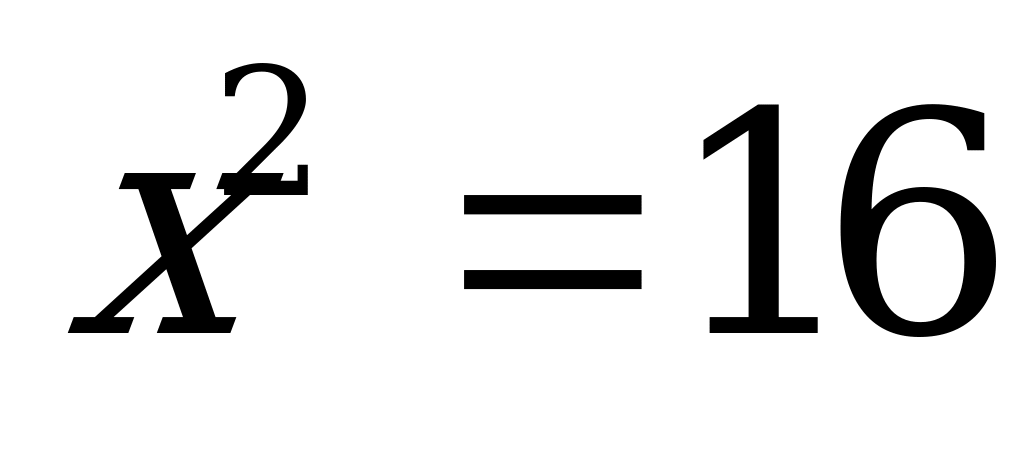 . «Длина поля равна 4» - указано в папирусе.
. «Длина поля равна 4» - указано в папирусе.
Прошли тысячелетия, в алгебру вошли отрицательные числа. Решая уравнение 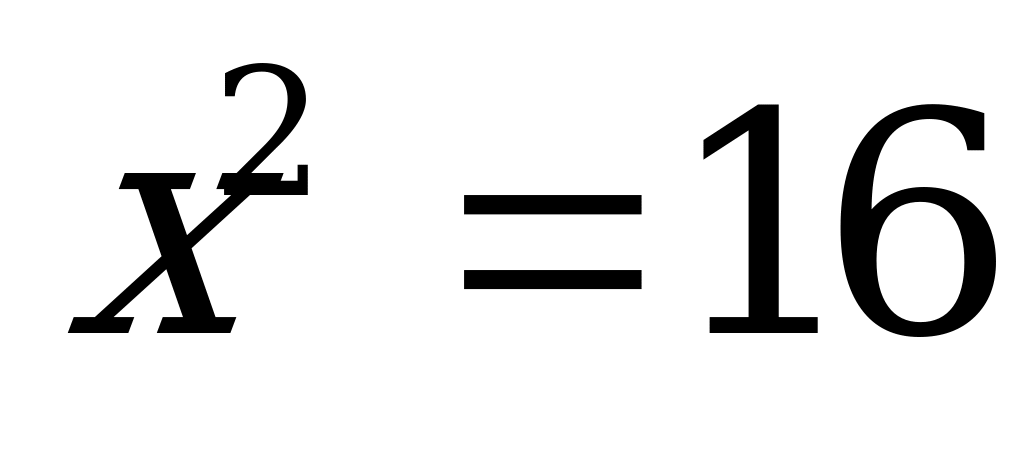 мы получаем два числа:
мы получаем два числа: 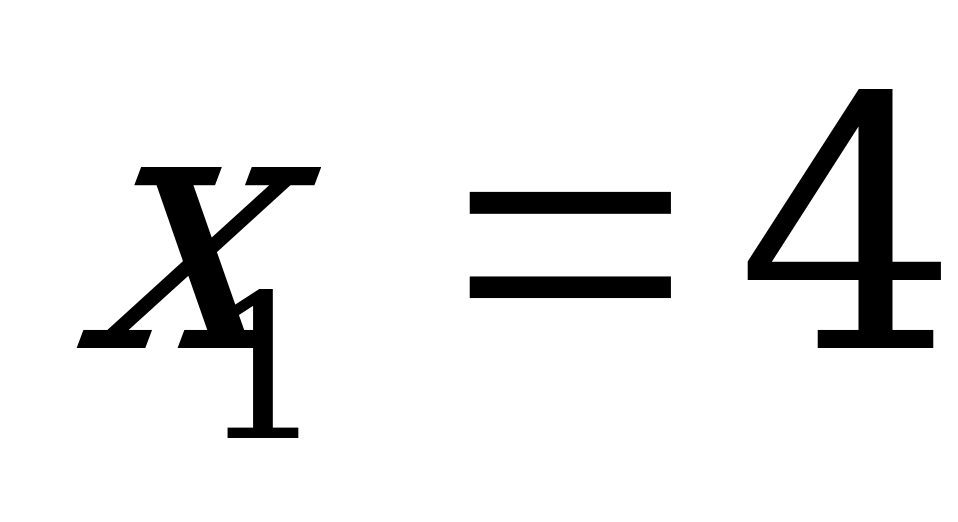 и
и 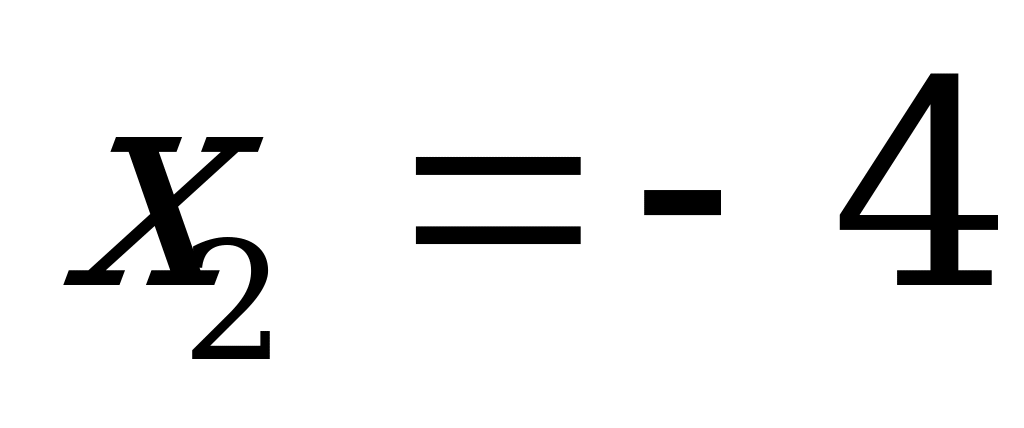 . Разумеется в египетской задаче и мы приняли бы
. Разумеется в египетской задаче и мы приняли бы 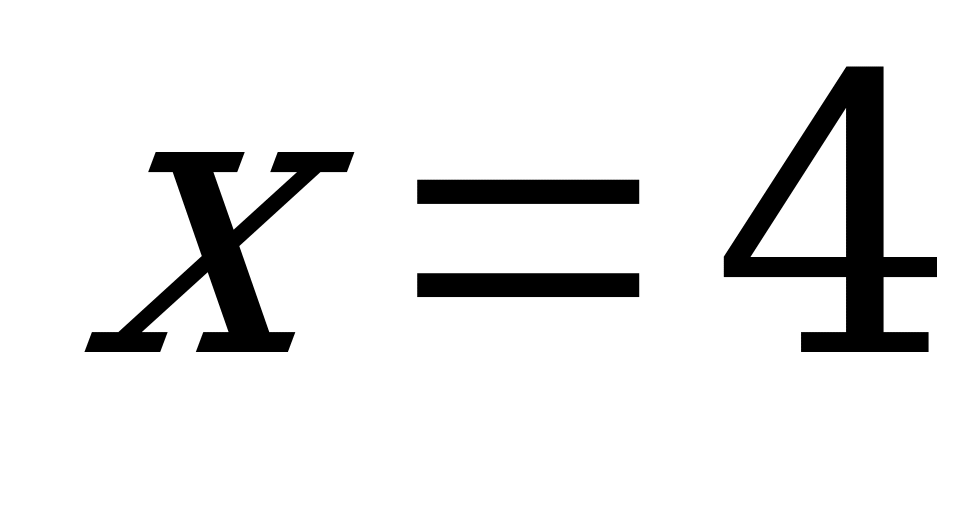 , т.к. длина поля может быть только положительной величиной.
, т.к. длина поля может быть только положительной величиной.
Огромный шаг вперед по сравнению с математиками Египта сделали ученые Междуречья. Они нашли правило для решения приведенного квадратного уравнения 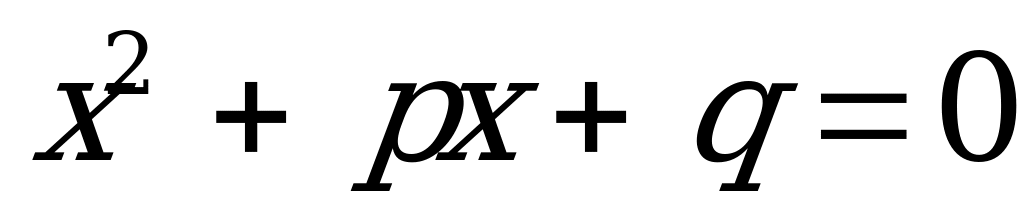 , где
, где 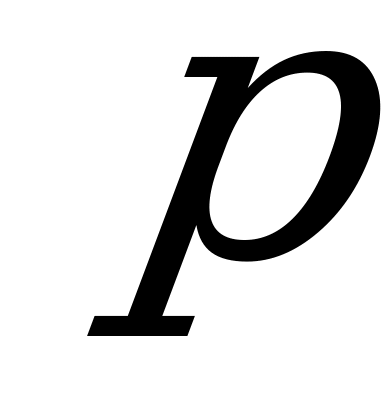 и
и 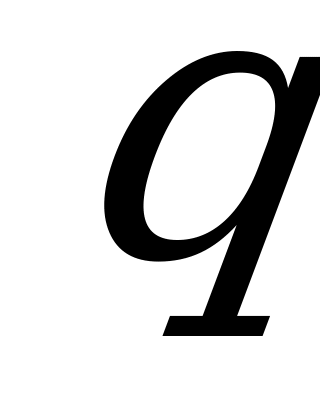 - любые действительные числа..
- любые действительные числа..
В одной из вавилонских задач так же требовалось определить длину прямоугольного поля 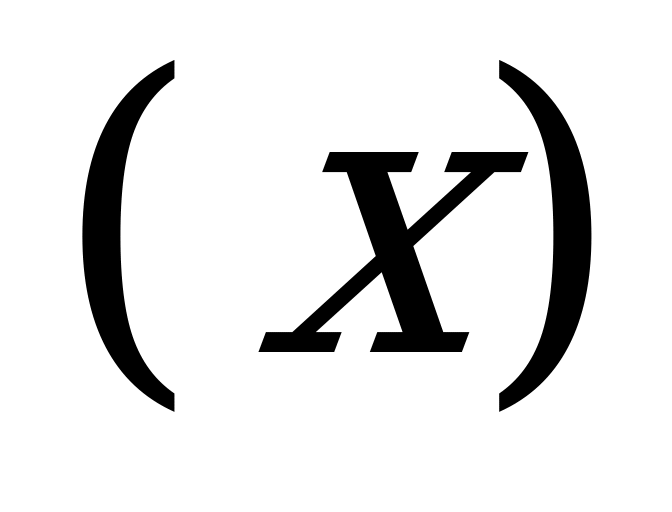 и его ширину
и его ширину 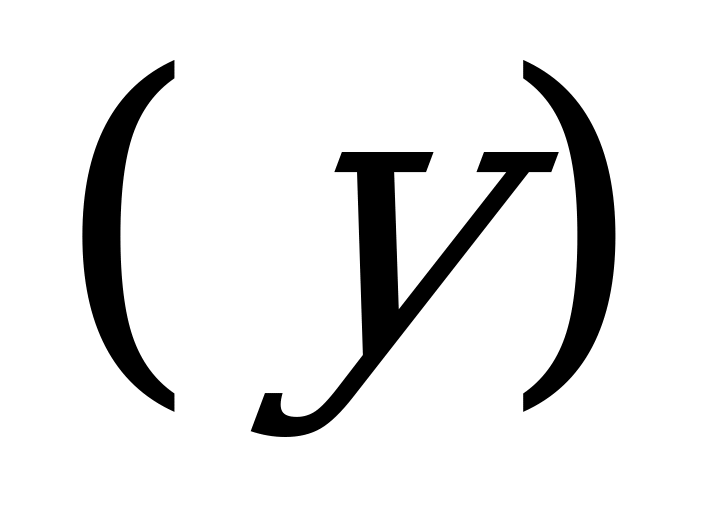 : «Сложив длину и две ширины прямоугольного поля, получишь 14, а площадь поля 24. Найди его стороны».
: «Сложив длину и две ширины прямоугольного поля, получишь 14, а площадь поля 24. Найди его стороны».
Составим систему уравнений: 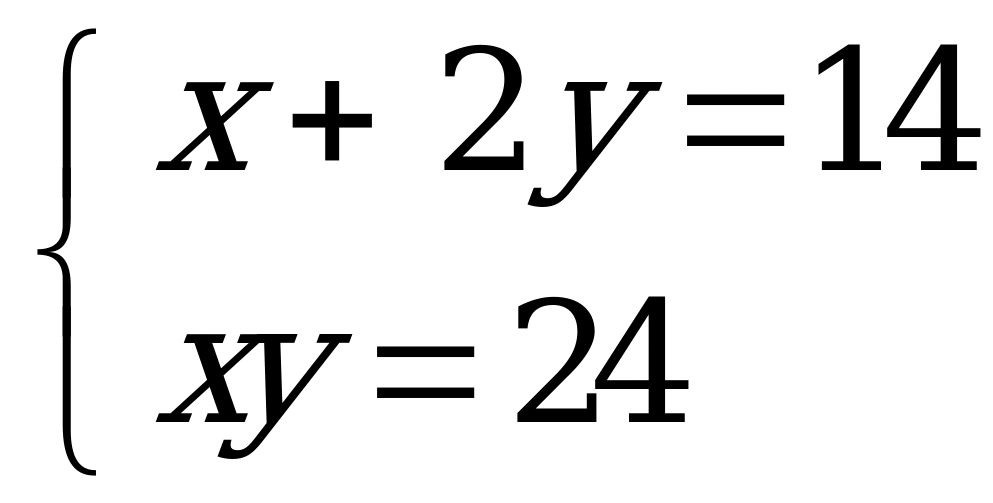
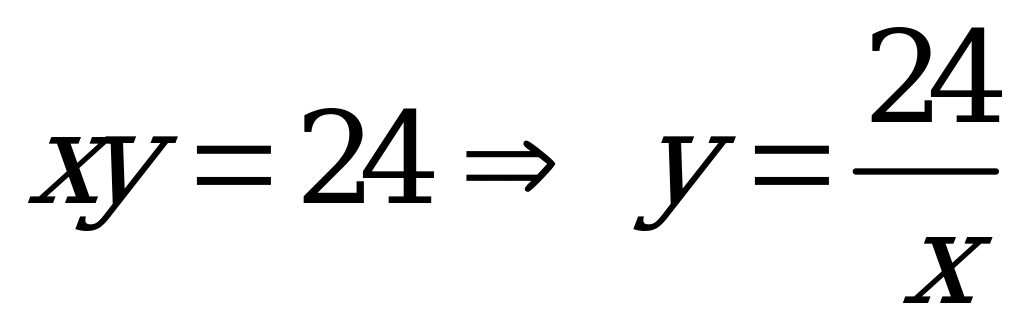 и подставим в первое уравнение:
и подставим в первое уравнение:
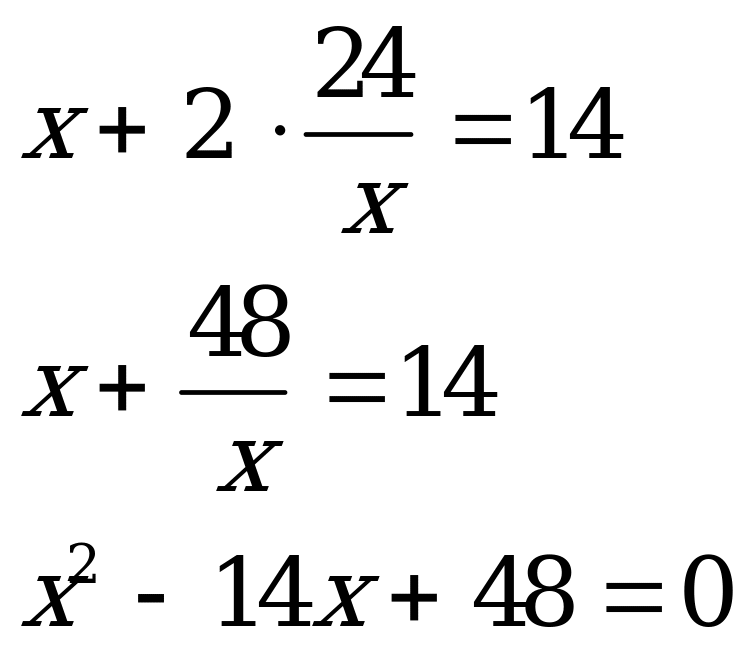
Для его решения прибавили к выражению 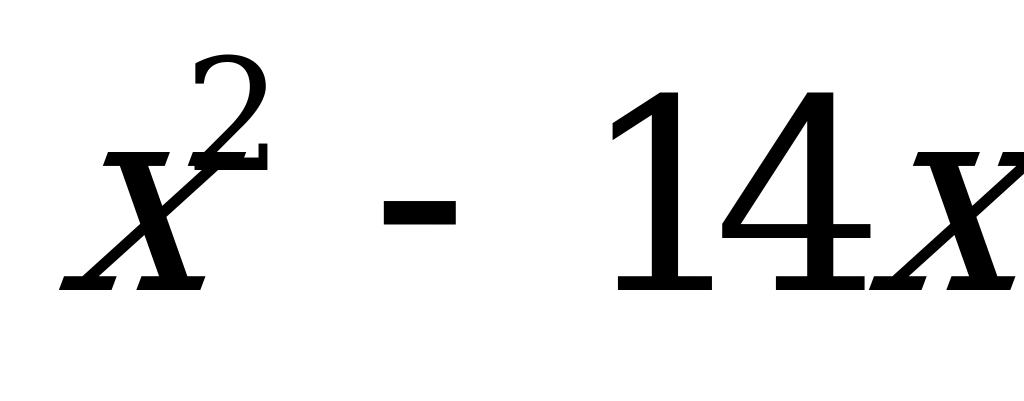 некоторое число, чтобы получить полный квадрат:
некоторое число, чтобы получить полный квадрат: 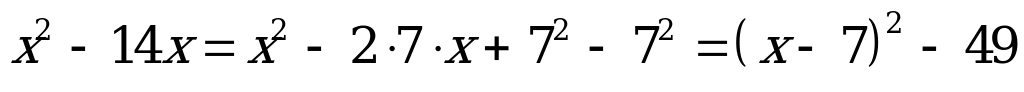 .
.
Теперь уравнение можно записать так:
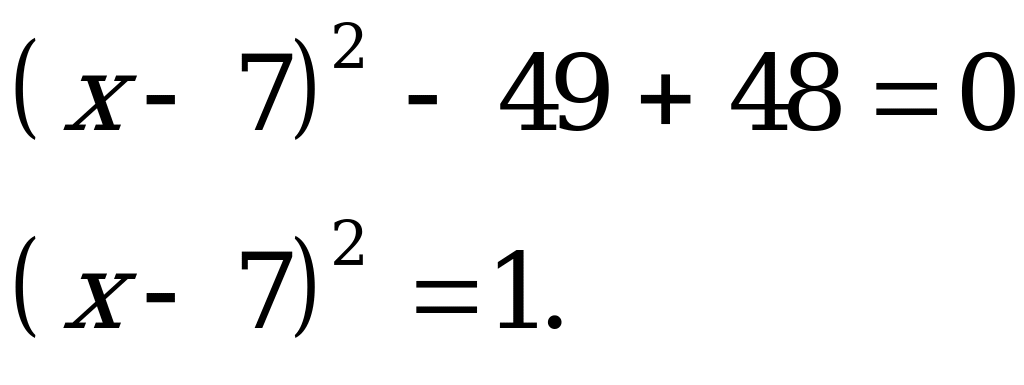
Мы пришли к квадратному уравнению, которое умели решать и египтяне. Не зная отрицательных чисел, древние математики получали:
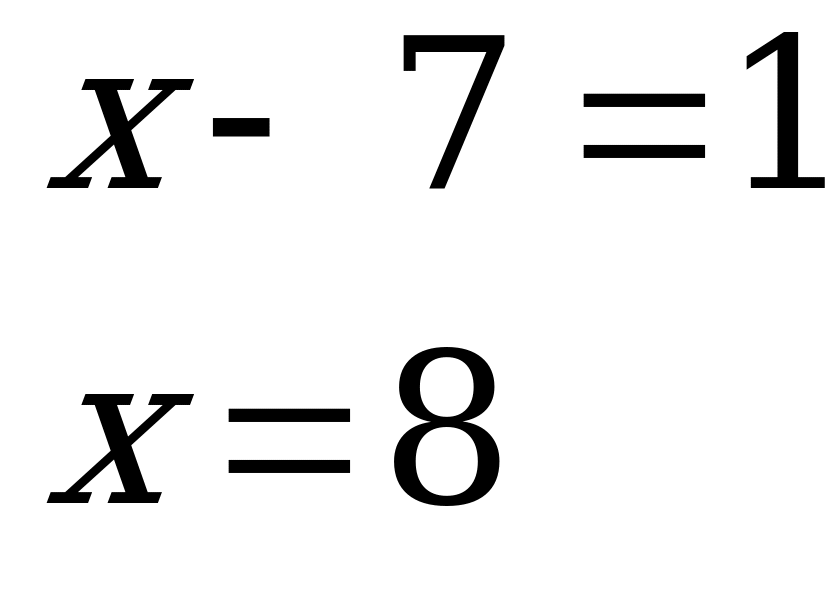
Следовательно, 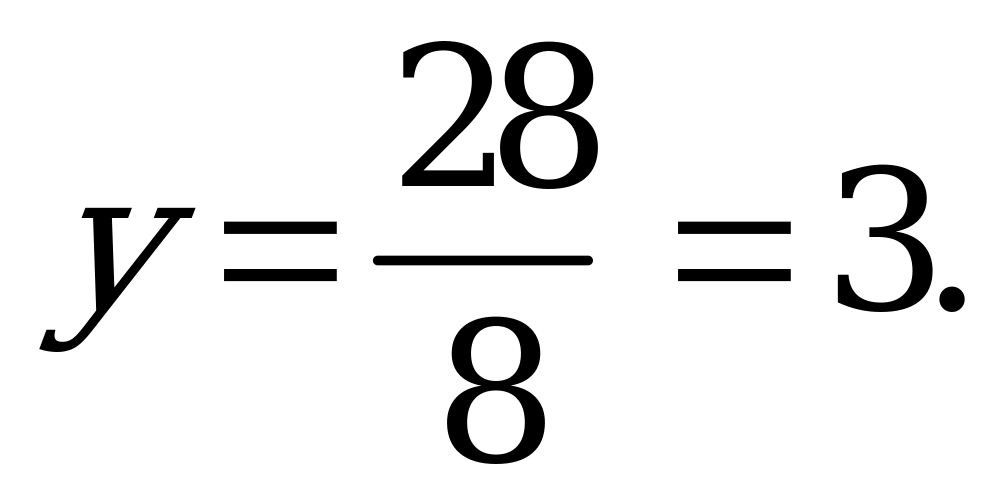 Т.е. длина поля равна 8, а ширина поля равна 3.
Т.е. длина поля равна 8, а ширина поля равна 3.
Вообще же квадратное уравнение 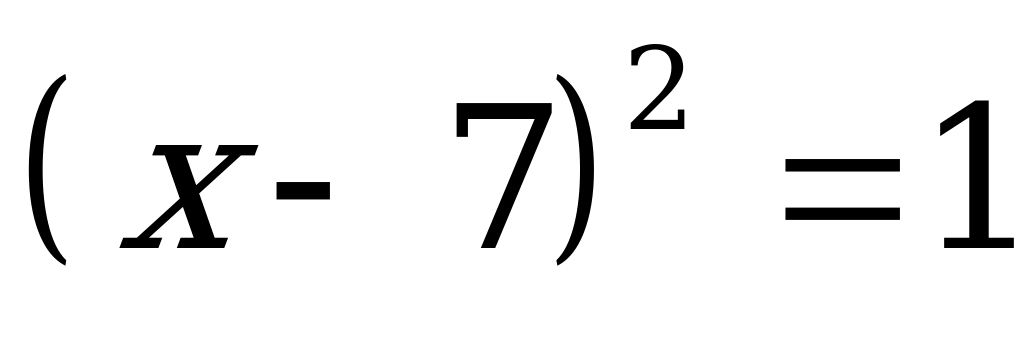 имеет два корня:
имеет два корня:
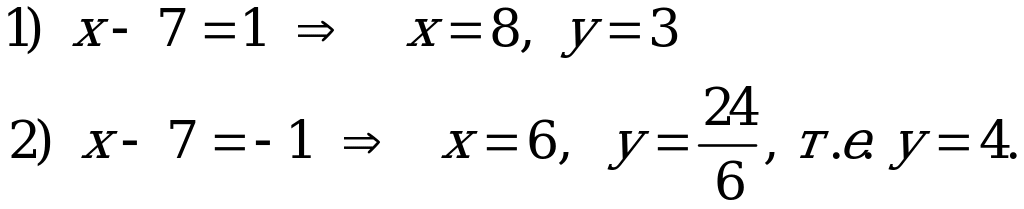
На предыдущем уроке мы познакомились с методом выделения полного квадрата для решения квадратных уравнений. Чтобы каждый раз не проводить большие вычисления, нам достаточно решить уравнение один раз и получить готовые формулы для корней квадратного уравнения.
Сначала посмотрим, от чего зависит число корней квадратного уравнения.
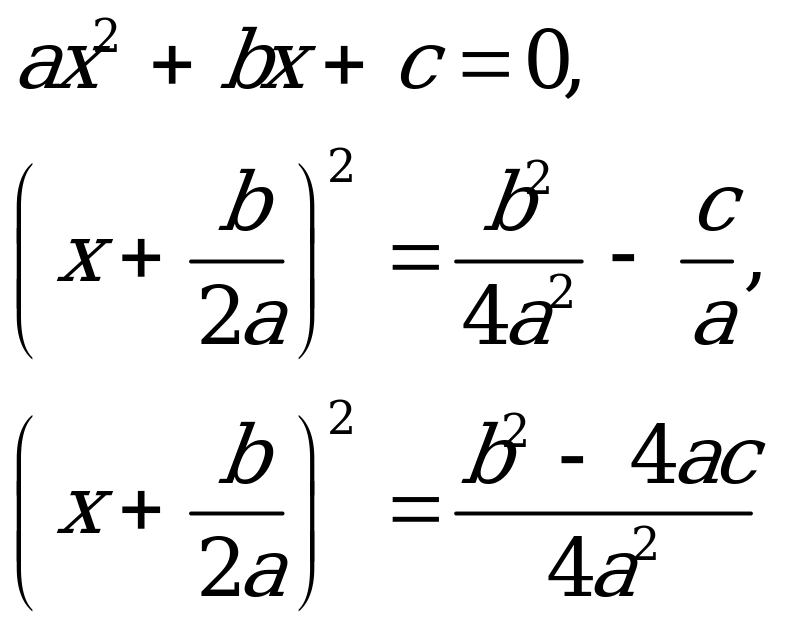
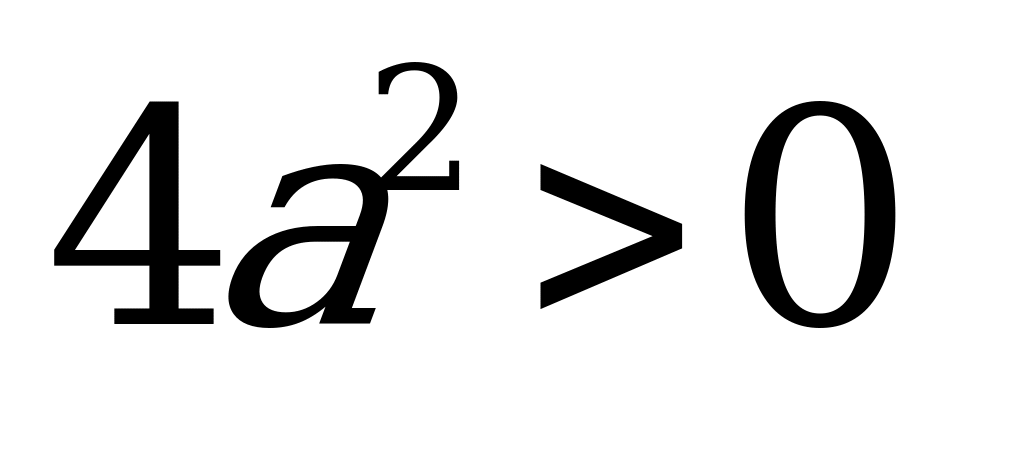 всегда, следовательно, от знака числителя
всегда, следовательно, от знака числителя
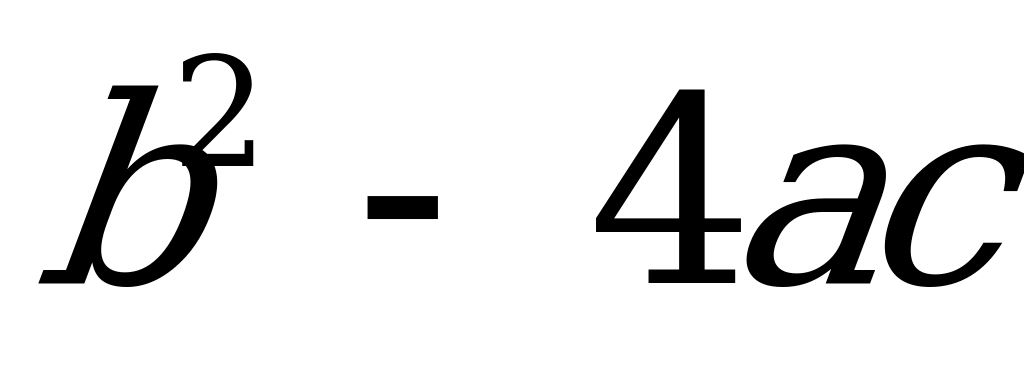 зависит число корней квадратного уравнения.
зависит число корней квадратного уравнения.
Поэтому он удостоился собственного имени.
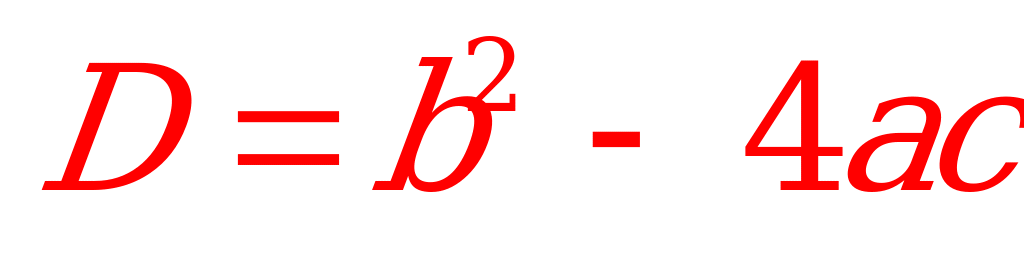
- дискриминант квадратного уравнения
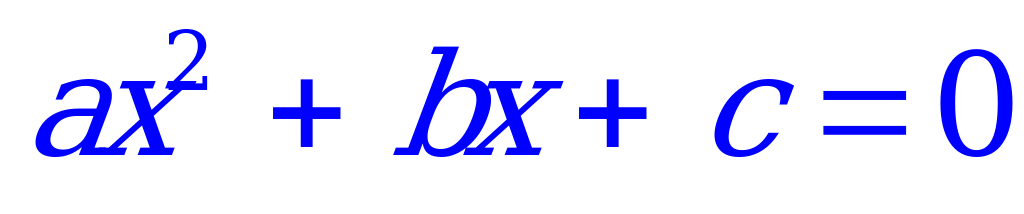
Возможны 3 случая:
1
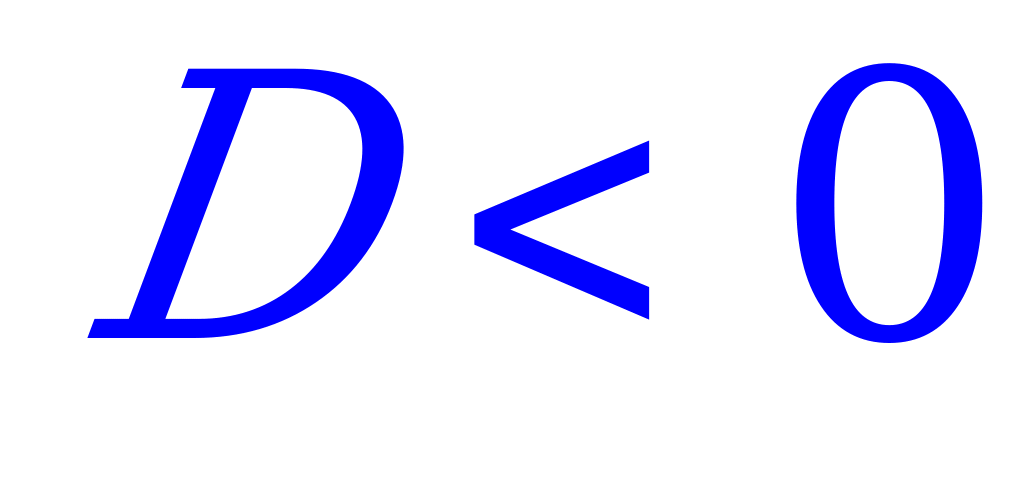 - корней нет
- корней нет
случай:
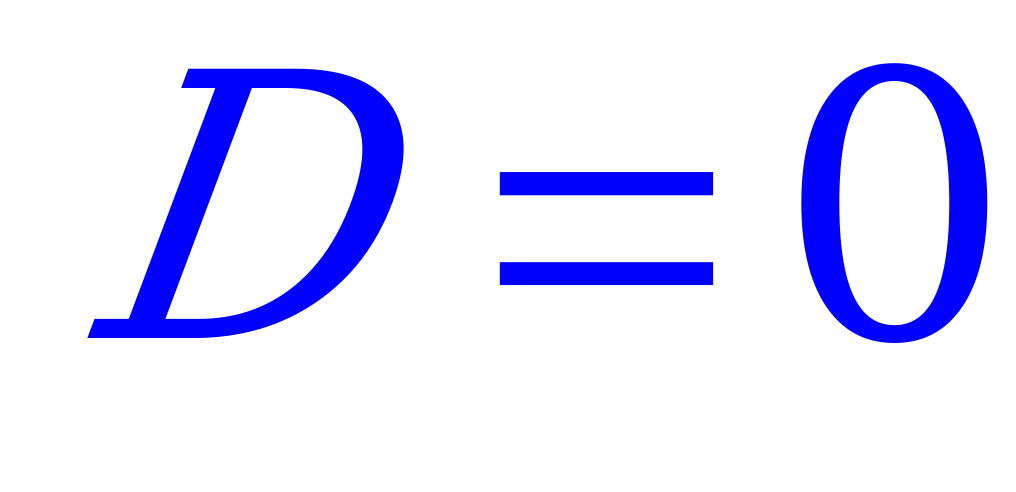 - один корень
- один корень
2
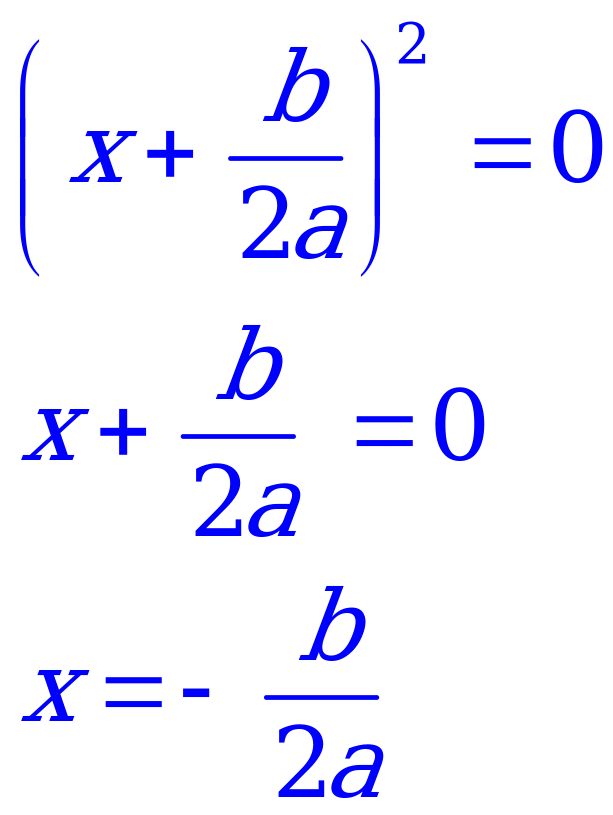
случай:
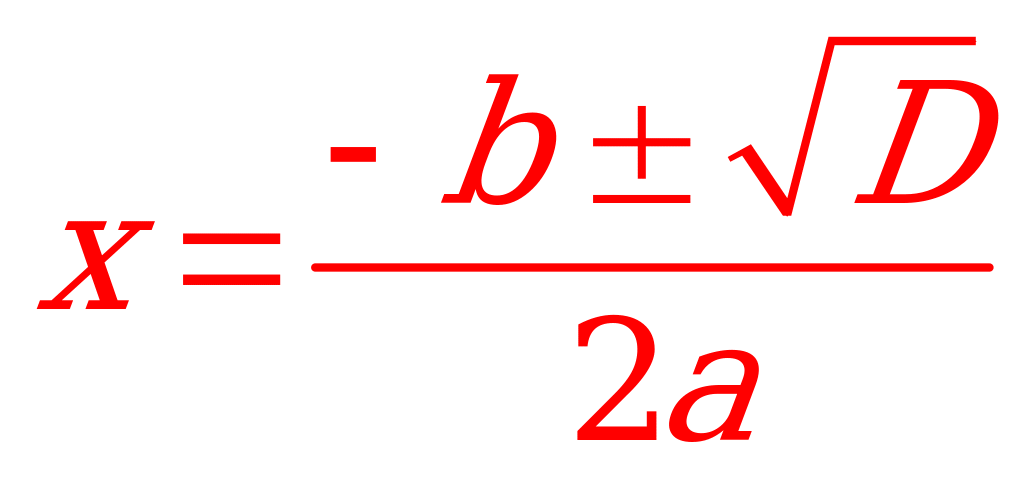
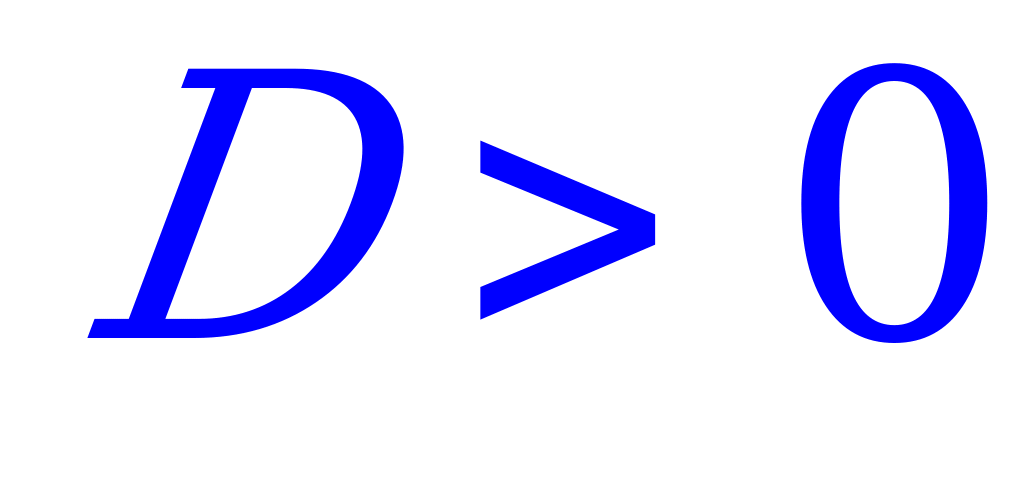 - два корня
- два корня
3 случай:
Закрепление изложенного материала.
Учащиеся решают уравнения:
№1. Решите уравнения:
| 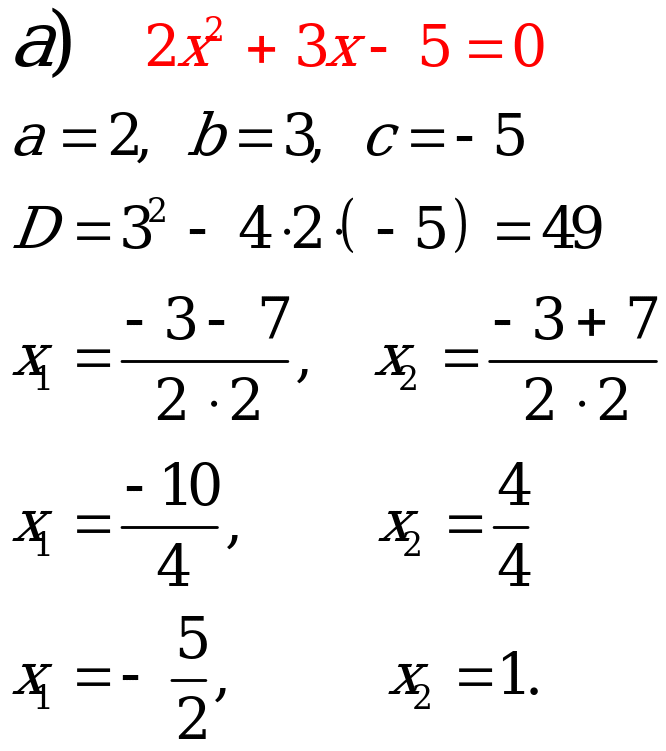
Ответ:  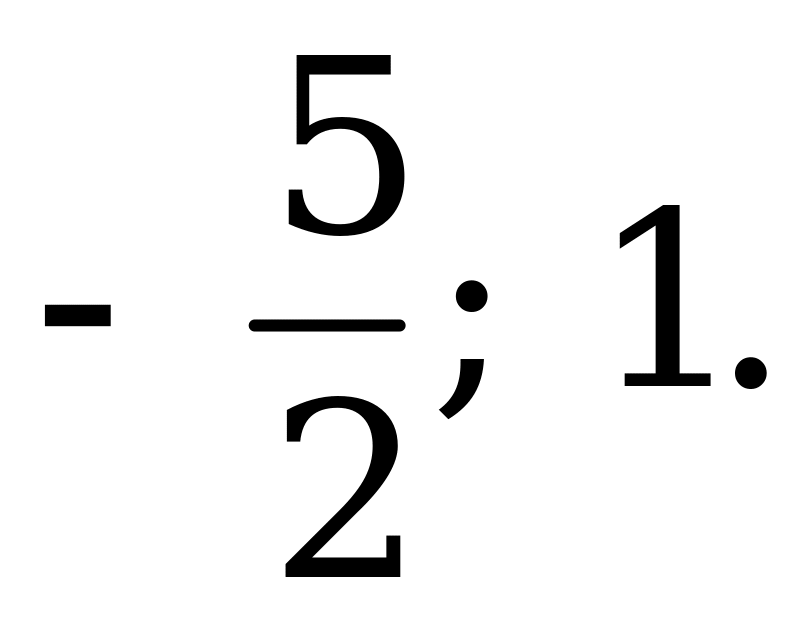 | 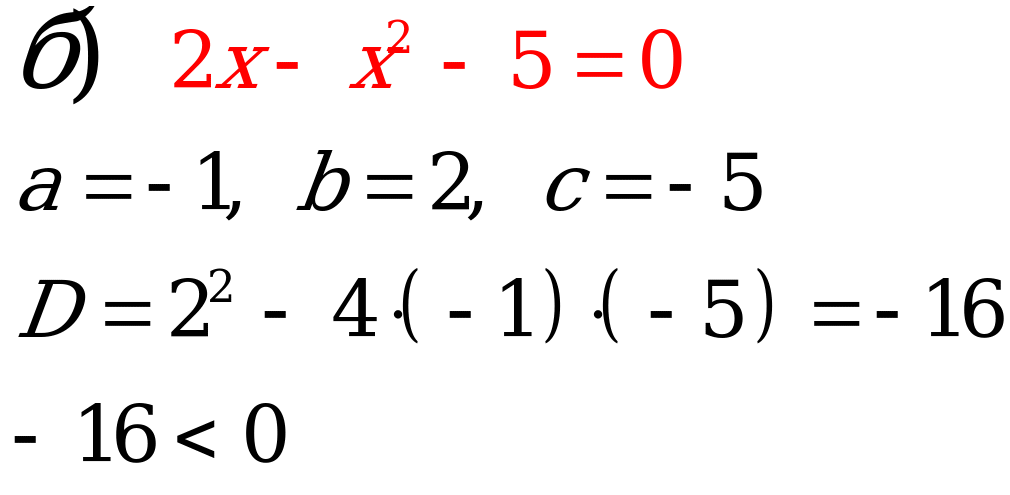
корней нет
Ответ:  корней нет. корней нет. | 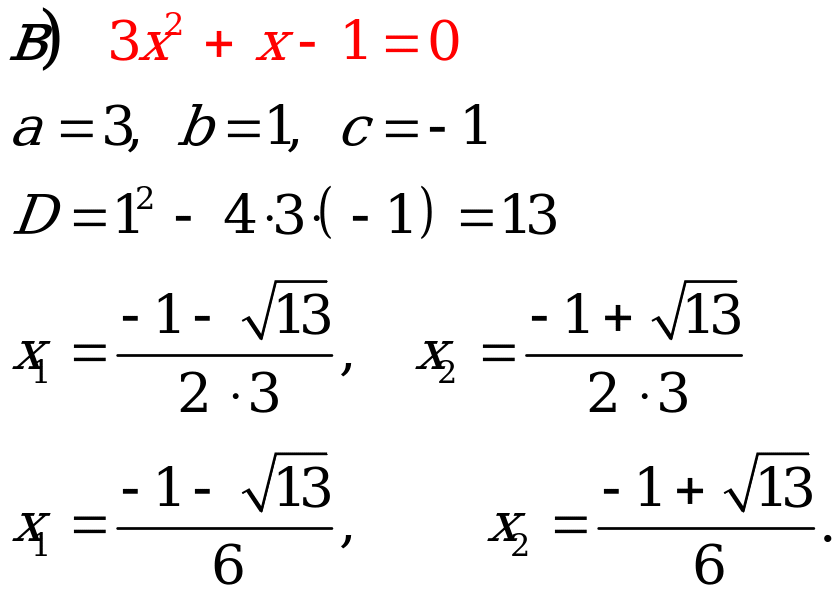
Ответ:  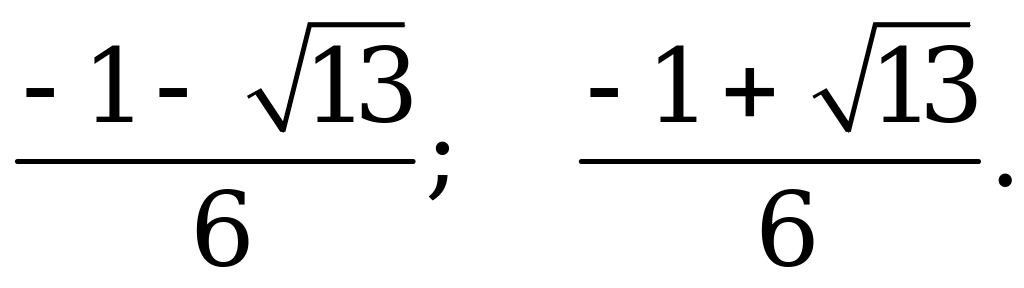 |
№2. Вычислите дискриминант квадратного уравнения.
Учащиеся самостоятельно вычисляют дискриминант квадратного уравнения.
| 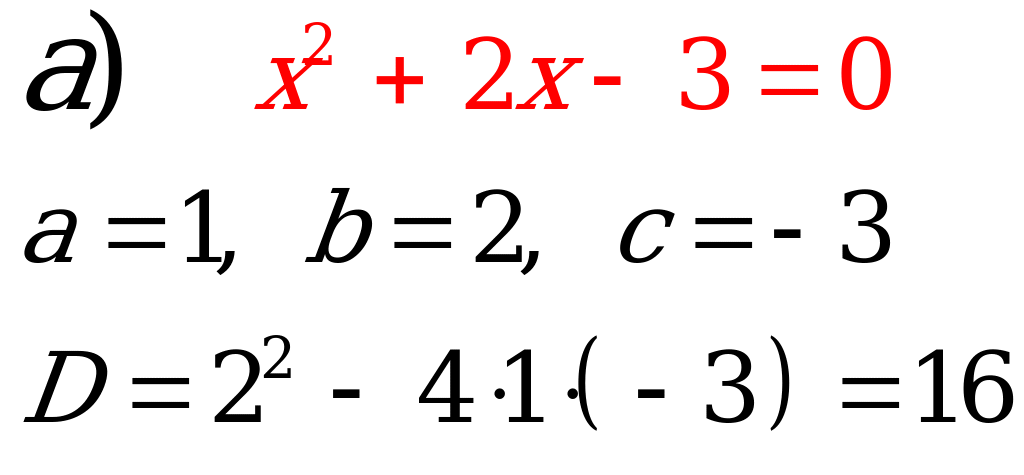
Ответ:  16. 16. | 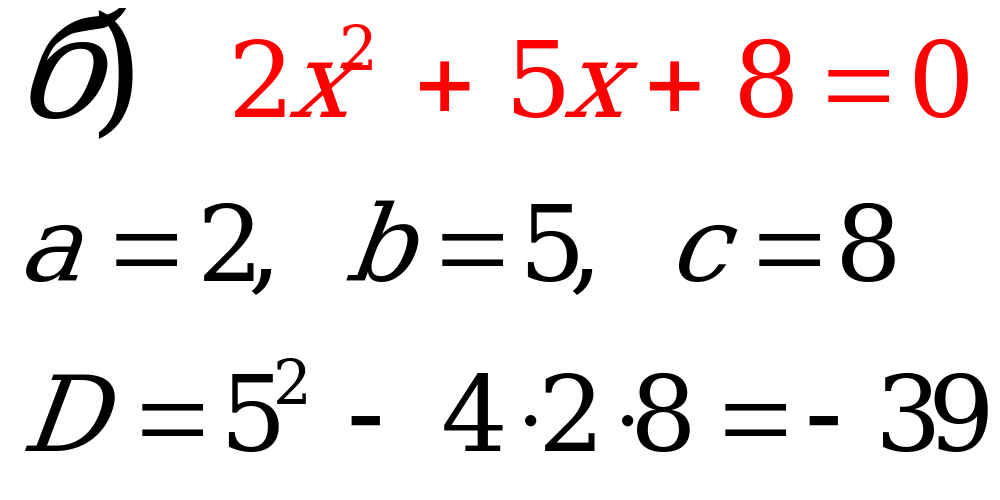
Ответ: - 39. | 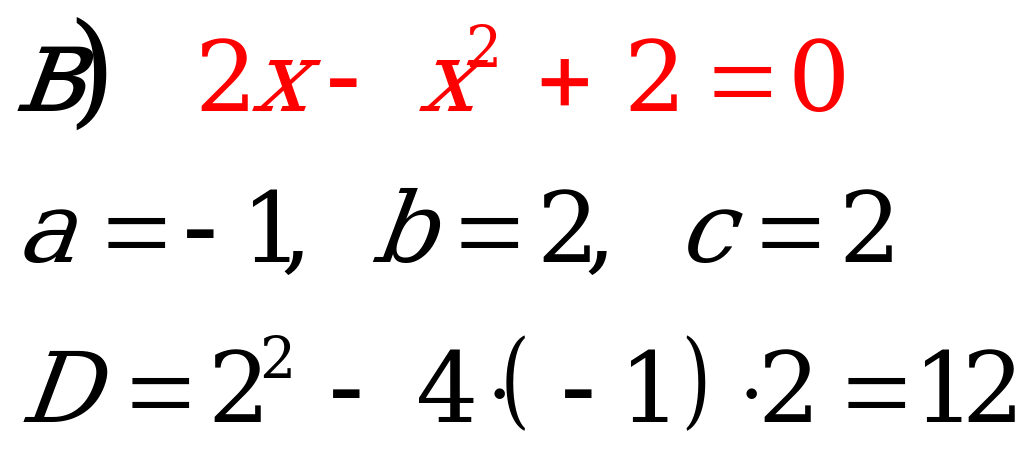
Ответ: 12.  |
№3. Определите количество корней квадратного уравнения.
Вопрос учителя: От чего зависит количество корней квадратного уравнения?
| 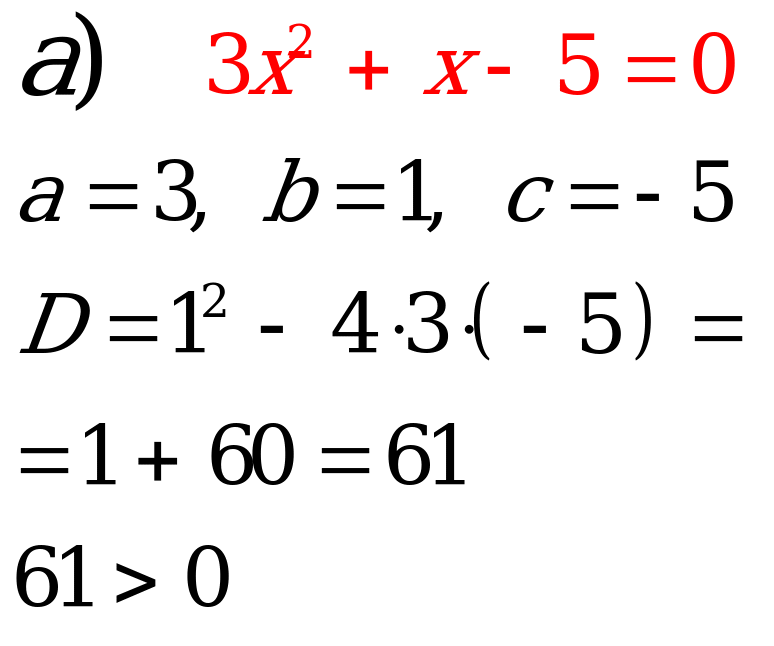
2 корня
Ответ: 2 корня. | 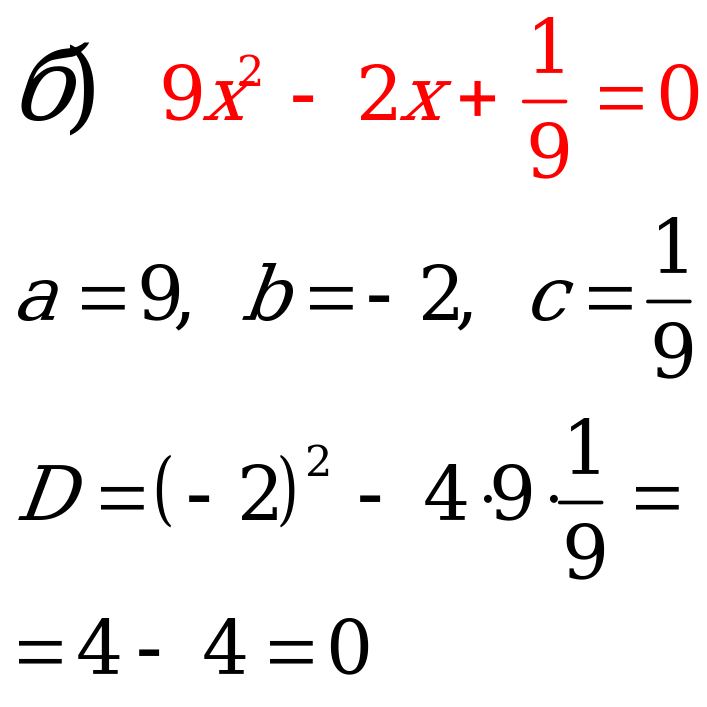
1 корень
Ответ: 1 корень. | 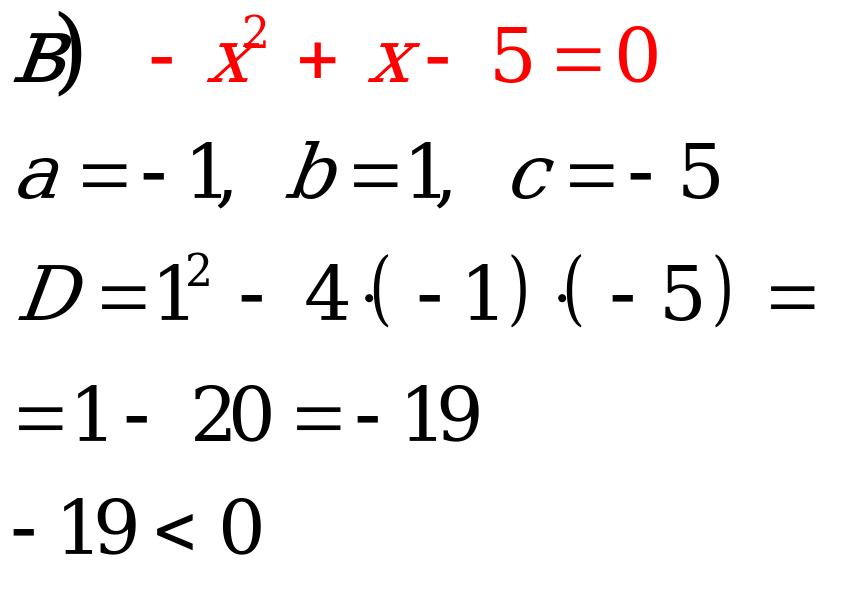
нет корней
Ответ: нет корней .  |
№4. Решите квадратное уравнение:
| 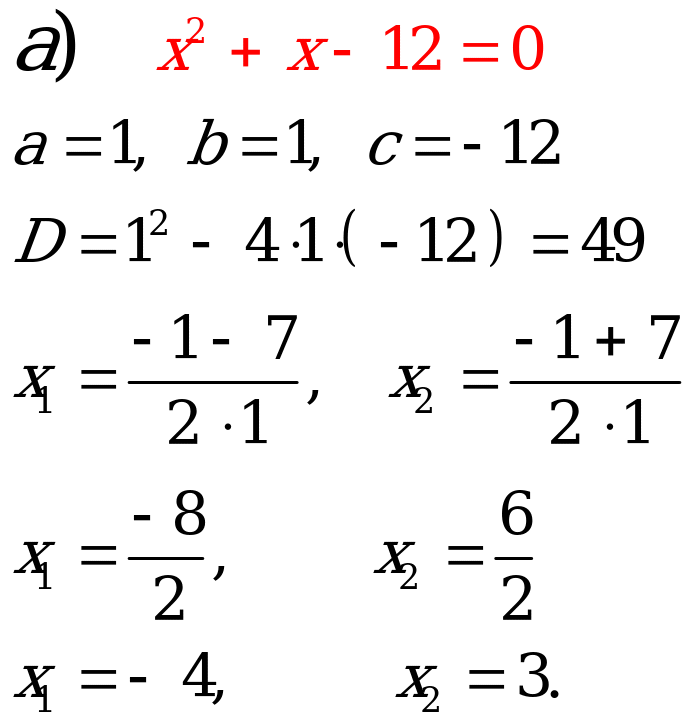
Ответ:  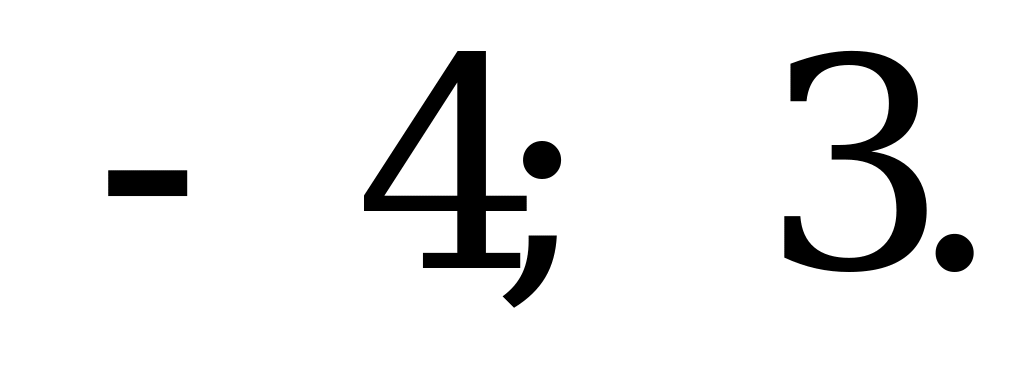 | 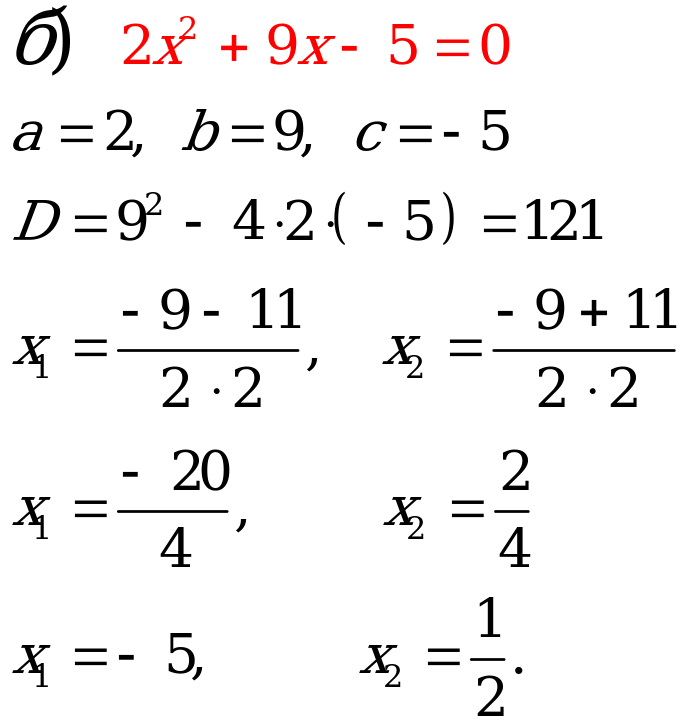
Ответ:  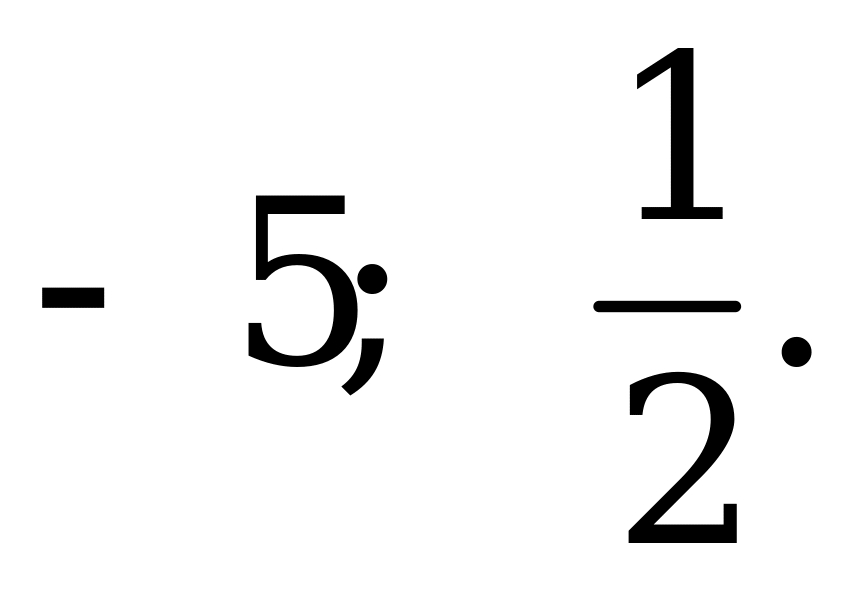 |
| 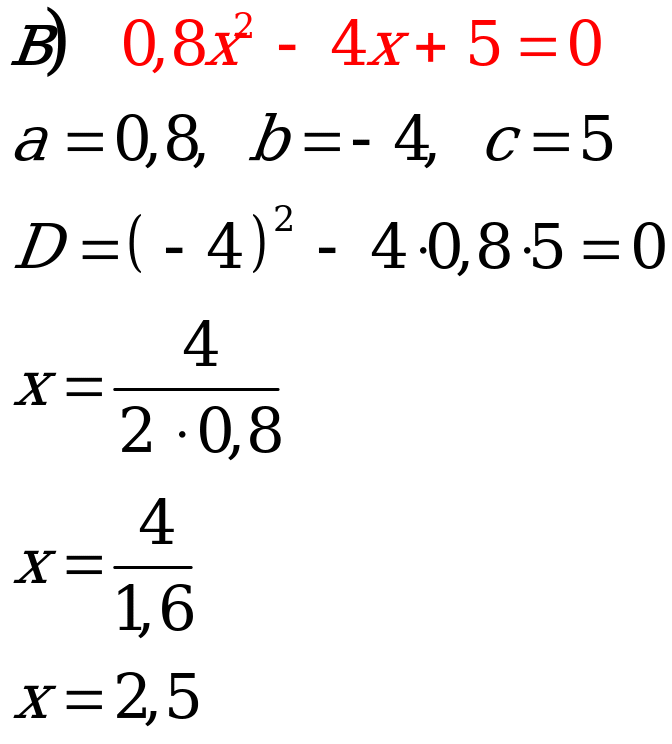
Ответ:  2,5. 2,5. | 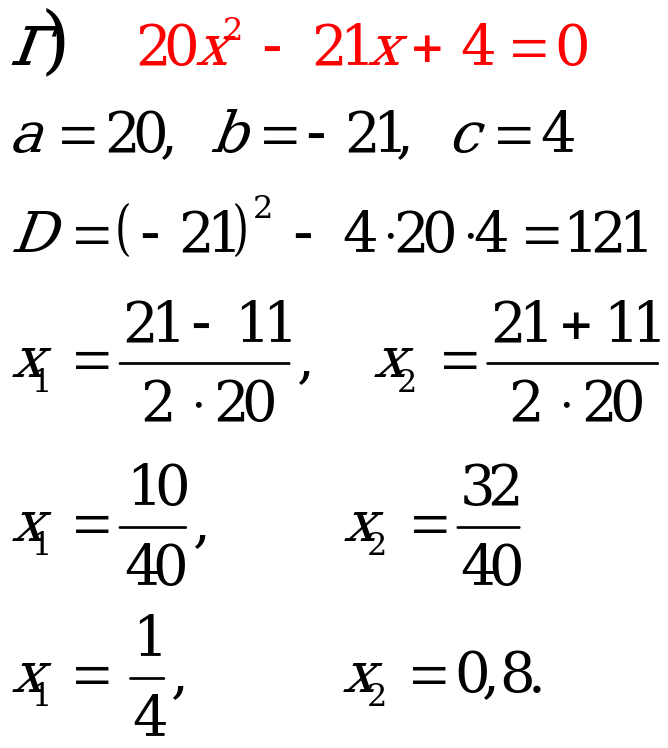
Ответ:  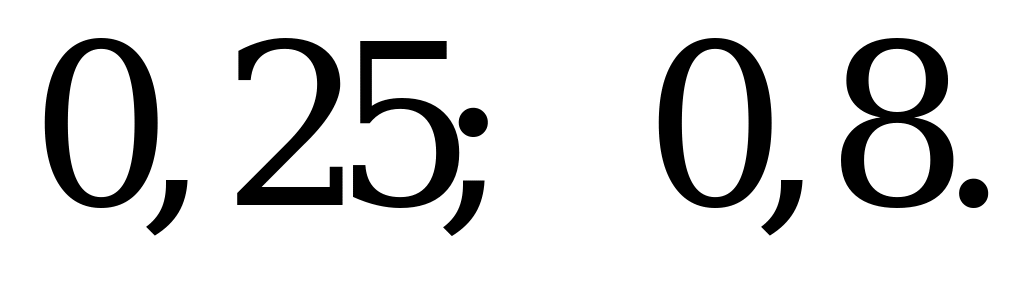 |
Казалось бы все случаи разобраны, формулы выведены. Но математик то ли от лени, толи из экономии времени продолжали облегчать себе пути нахождения корней квадратного уравнения.
Во-первых, говорили они, зачем запоминать две формулы для случаев 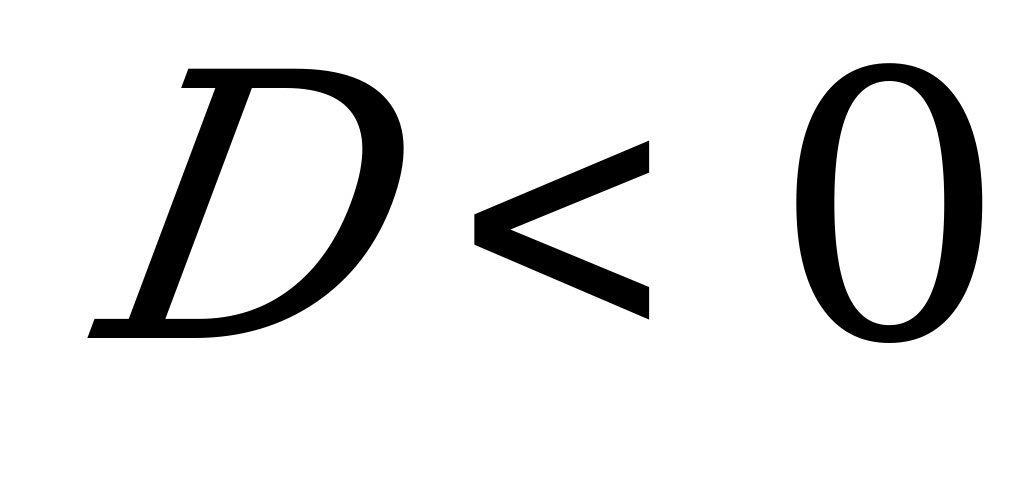 и
и 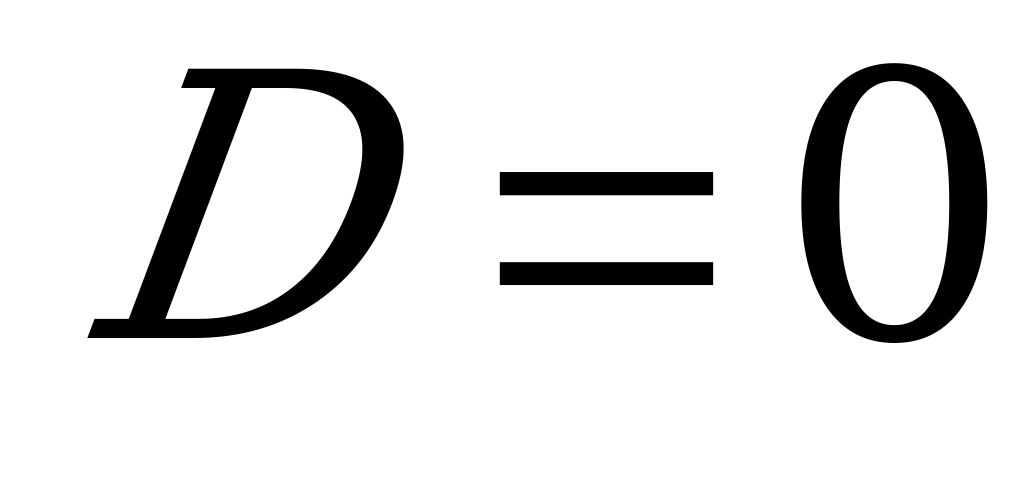 , когда это одна и та же формула.
, когда это одна и та же формула.
Во-вторых, математики заметили, что эту формулу можно еще больше упростить, когда второй коэффициент является четным числом.
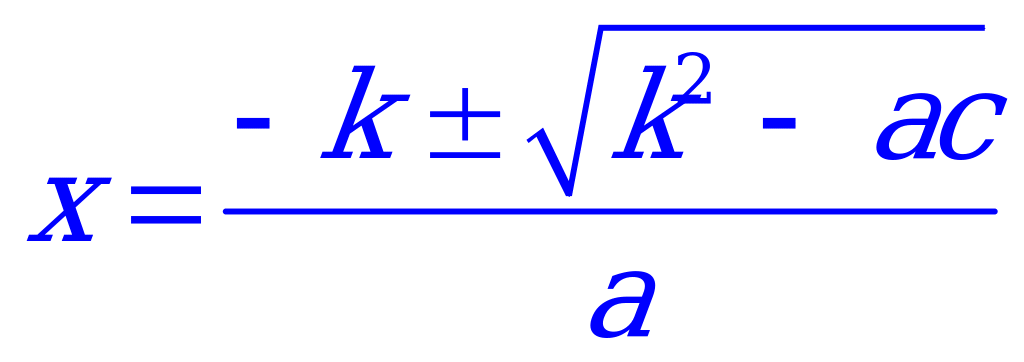
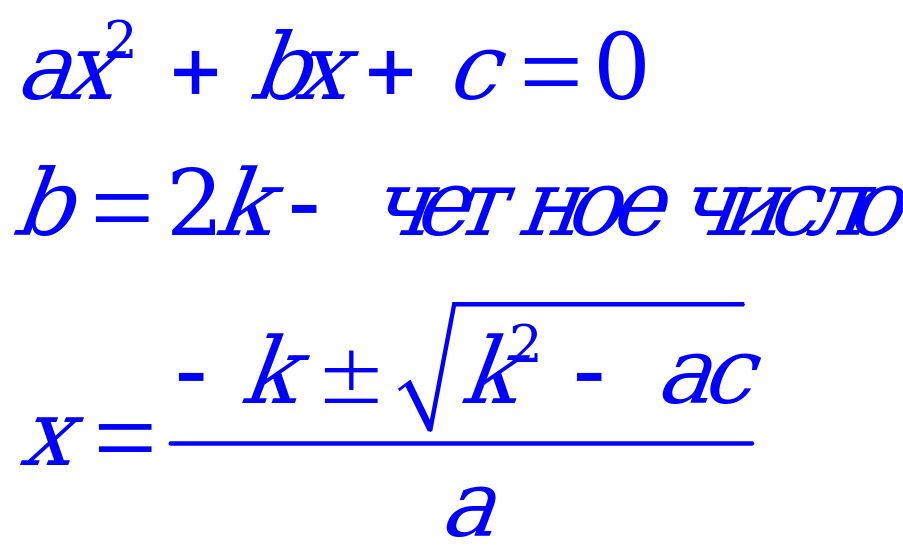
- формула корней квадратного уравнения
с четным вторым коэффициентом
3. Решение упражнений из учебника: №534 (а, г, е, ж), №537 (а, б).
4. Итог урока.
5. Задание на дом: п. 21, №533, №534 (б, в, д, з), №543.