Урок в 9 классе

Урок алгебры в 9 классе по теме «Геометрическая прогрессия»

Учитель математики высшей квалификационной категории МБОУ СОШ №32 г. Новочеркасска Кручинина Вера Борисовна

2013 год

Девиз урока: «Нельзя быть любознательным с ленцой…»

Личностные цели

• Самостоятельно добывать знания.
• Уверенно и грамотно выражать свои мысли на математическом языке и языке формул.
• Правильно и последовательно выполнять алгебраические преобразования.
• Научиться ничего не принимать на веру.
• Не бояться ошибок, развивать умение отстаивать свое мнение.

Задание: напишите в один из столбиков любую последовательность чисел

• 2, 4, 6…
• - 1, 7, 23…
• 1, 2, 4, 7…
• 6, 6, 6, 6…
• -1, -2, -3…
• 3, 4, 6, 7…

• 3, 9, 27…
• 1, - 1, 1, - 1…
• 1, 3, 9, 27…
• 2, -4, 6, -8…
• 3, -3, 3, -3…
• 10, 9, 8, 7…

Задание: сравните математические объекты в каждой группе

Выбери меня, выбери меня…

«Математику нельзя изучать, наблюдая, как это делает сосед…» Айвен Нивен

Тема урока: «Геометрическая прогрессия»

Цель урока: сформулировать определение геометрической прогрессии, составить различные способы нахождения элементов геометрической прогрессии.

Математический диктант

• Задана последовательность чисел: 7, 11, 15… Указать четвертый член этой последовательности и ее вид.
• Запишите первые пять членов арифметической прогрессии, если известен ее первый член, он равен 8 и разность а.п, которая равна -3.
• Запишите первые четыре члена последовательности, если известен ее первый член, он равен 27 и каждый следующий меньше предыдущего в 3 раза.
• Дана последовательность чисел: 2, 4, 8, 16… укажите закономерность, по которой находят ее члены.
• Найдите произведение второго и четвертого членов этой последовательности, извлеките корень из полученного произведения, какому члену последовательности равен поученный результат?

Проверка выполнения

• 19, арифметическая прогрессия.
• 8, 5, 2, -1, -4.
• 27, 9, 3, 1.
• Каждый следующий член больше предыдущего в 2 раза.
• 64, 8, третьему члену.

Определение геометрической прогрессии

Ученик:

Автор:

Последовательность, в которой каждый следующий ее член изменяется в несколько раз называется геометрической прогрессией

Числовая последовательность

называется геометрической прогрессией, если для всех натуральных n выполняется равенство

q – некоторое число, неравное нулю.

Основное свойство геометрической прогрессии

Ученик:

Автор:

Если взять три последовательных члена г.п., то средний из них равен квадратному корню из произведения соседних с ним членов.

Если все члены прогрессии положительны, то каждый член г.п., начиная со второго, равен среднему геометрическому двух соседних с ним членов.

Физкультминутка

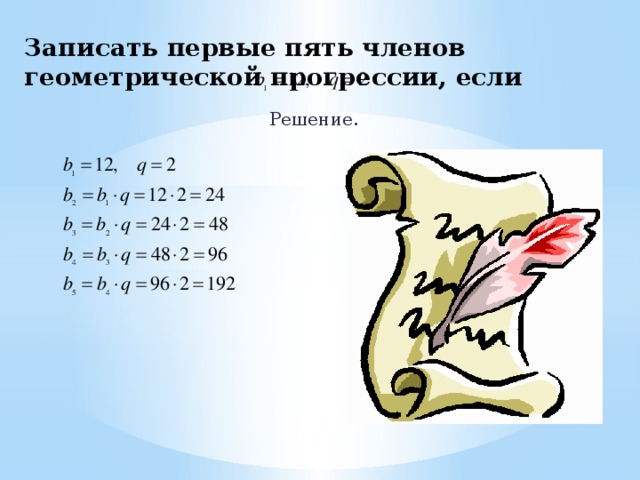
Записать первые пять членов геометрической прогрессии, если

Решение.

Задача №1 Решить самостоятельно: записать первые четыре члена г.п.

Решение.

Определите вид последовательности

• 1;2;3;4;5;…
• -2;-4;-8;-16;…
• 7;7;7;7;…
• 10;1;0,1;0,01;…
• -5;10;-20;40;-80 ;…

d=1

q=2

d=0 q=1

q=0,1

q=-2

Задача № 2

Величины углов выпуклого четырехугольника образуют геометрическую прогрессию со знаменателем 2.Найдите эти углы.

Выберите утверждение, которое подходит вам

• Было интересно и все понятно.
• Интересно, но испытываю небольшие затруднения.
• Многое непонятно, нужна помощь.

д/з: п.20 стр.101, № 271, №319 (по желанию)

А теперь, в конце урока хочется, чтобы вы выразили свое отношение к нашей сегодняшней работе и всему уроку в целом. Ответьте на вопросы в листах рефлексии и сдайте их мне.

Спасибо за внимание!