Урока по теме «Тетраэдр и параллелепипед» с использованием информационных технологий

Фрагмент урока по теме исследования с использованием информационных технологий

Тема: «Тетраэдр и параллелепипед»

Класс: 10 «А»

Тип урока: урок обобщения и систематизации знаний

Решение задач на построение сечений. Работа в программе GeoGebra.

Задача 72. Построить сечение пирамиды SABC плоскостью PQR, если точка P лежит на ребре SA, точка Q лежит на ребре SB, точка R лежит на ребре SC.

Решение (построение):

1. Запустить программу GeoGebra.

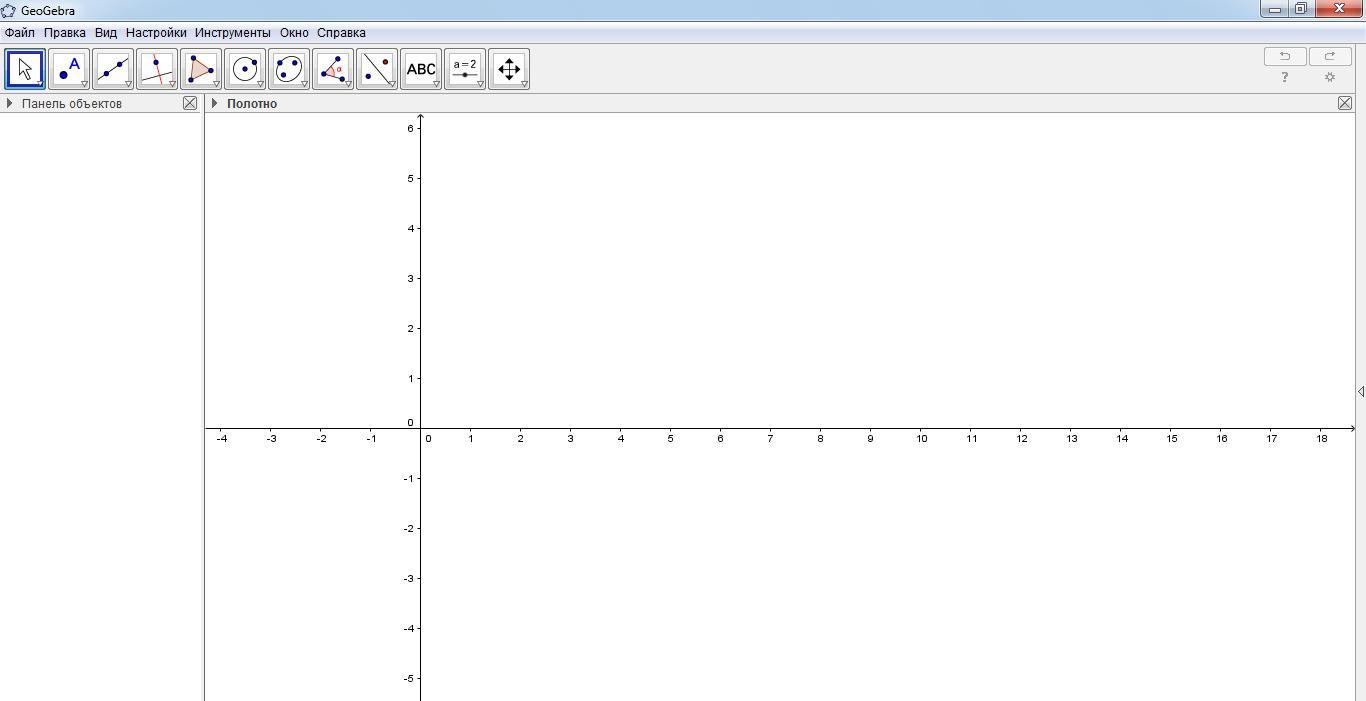
1. С помощью инструмента «Переместить чертеж» переместить оси координат так, как показано на рисунке (начало координат – в левом нижнем углу)

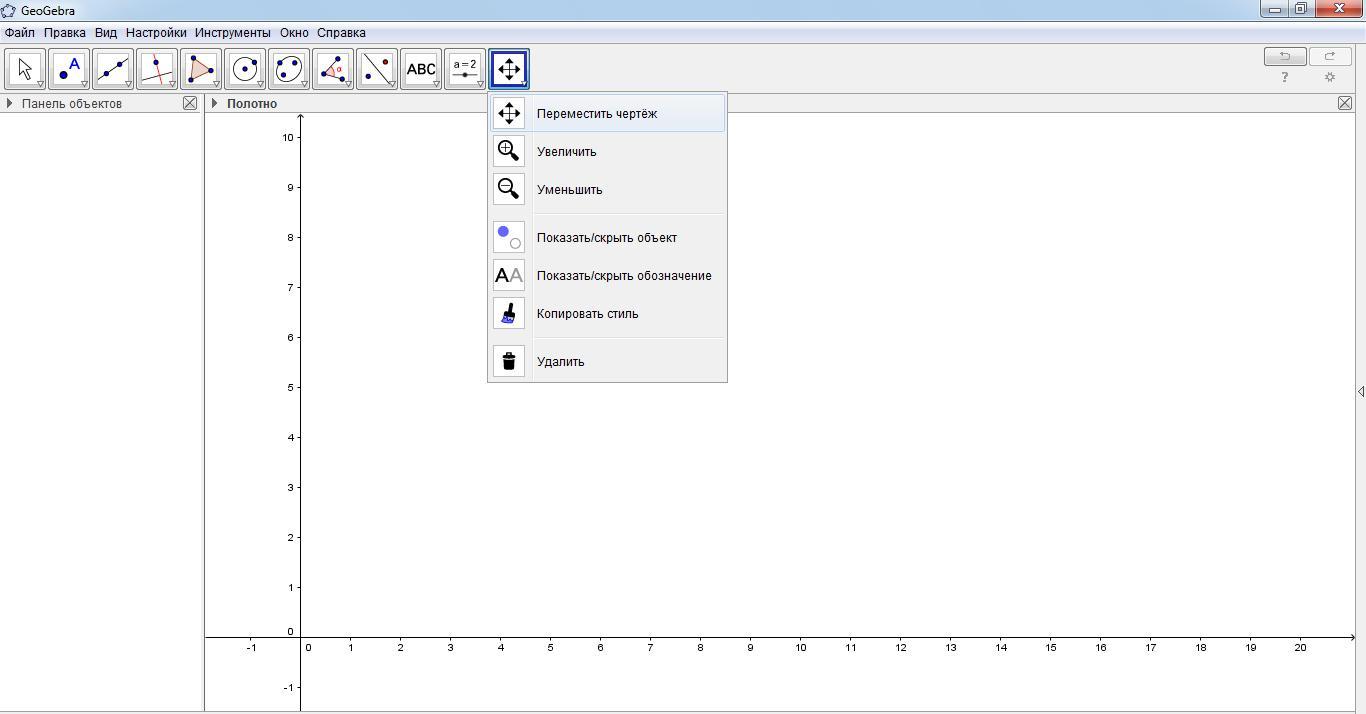
• Построить треугольную пирамиду SABC, как описано ниже и показано на рисунке, а именно: помощью инструмента «Многоугольник» построить треугольник при помощи щелчков левой кнопки мыши (четыре щелчка мыши – по очереди в точках A, B, C и снова в A, чтобы закончить контур треугольника, наименование точек программа производит самостоятельно).

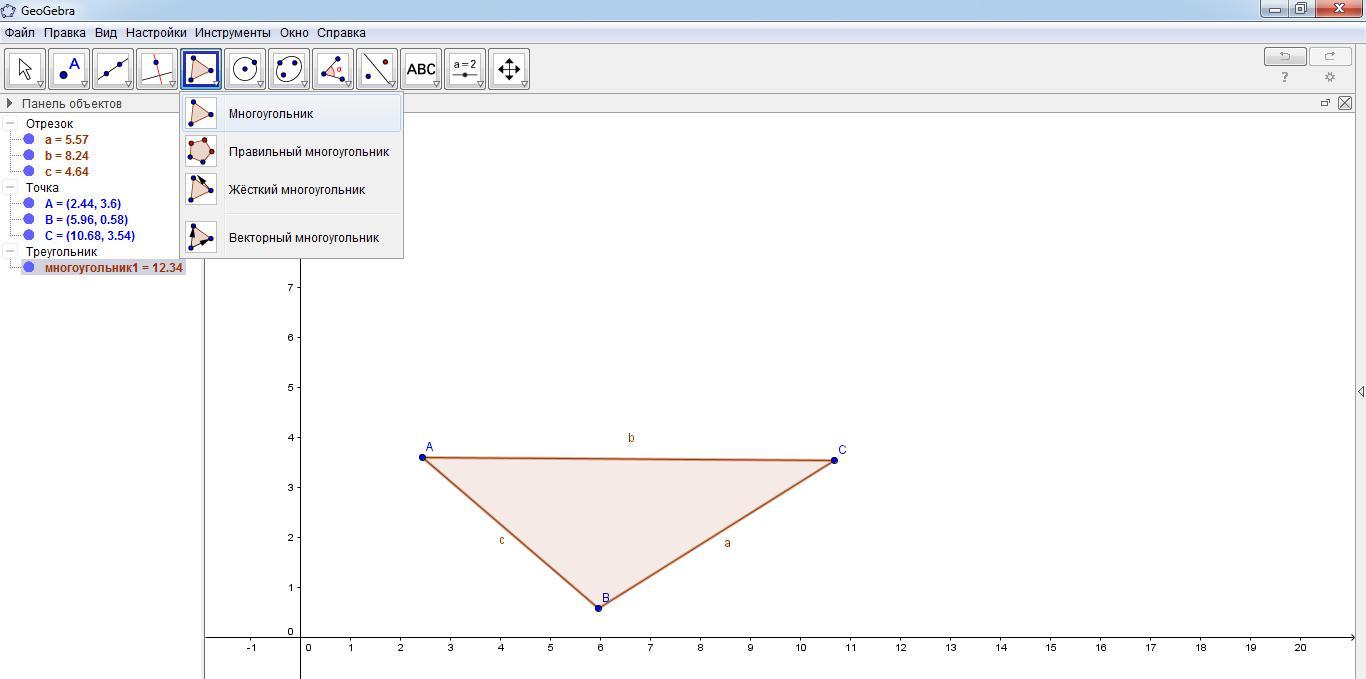
• помощью инструмента «Отрезок» построить ребра SA, SB, SC при помощи щелчков левой кнопки мыши (шесть щелчков мыши – в точках D, A, потом D, B и затем D, C и переименовать точку D в точку S при помощи нажатия на точке D правой кнопки мыши, выбора опции переименовать и ввода

нового имя точки S).

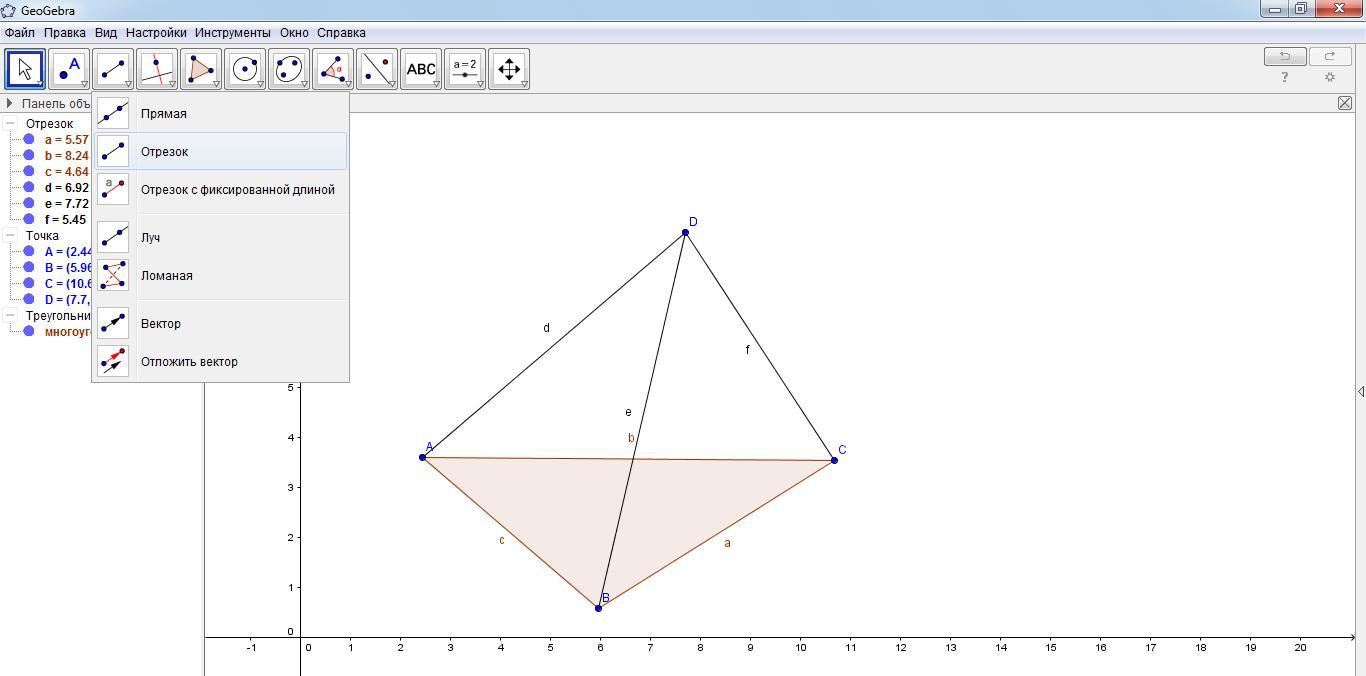
• осталось сделать невидимое ребро АС пунктирной линией. С помощью нажатия правой клавиши мыши на ребре АС выбрать свойства и в новом диалоговом окне выбрать стиль – стиль линии пунктирный и окно закрыть.

1. С помощью инструмента «Точка» отметить на ребре SA точку P, на ребре SB точку R, на ребре SC точку Q.

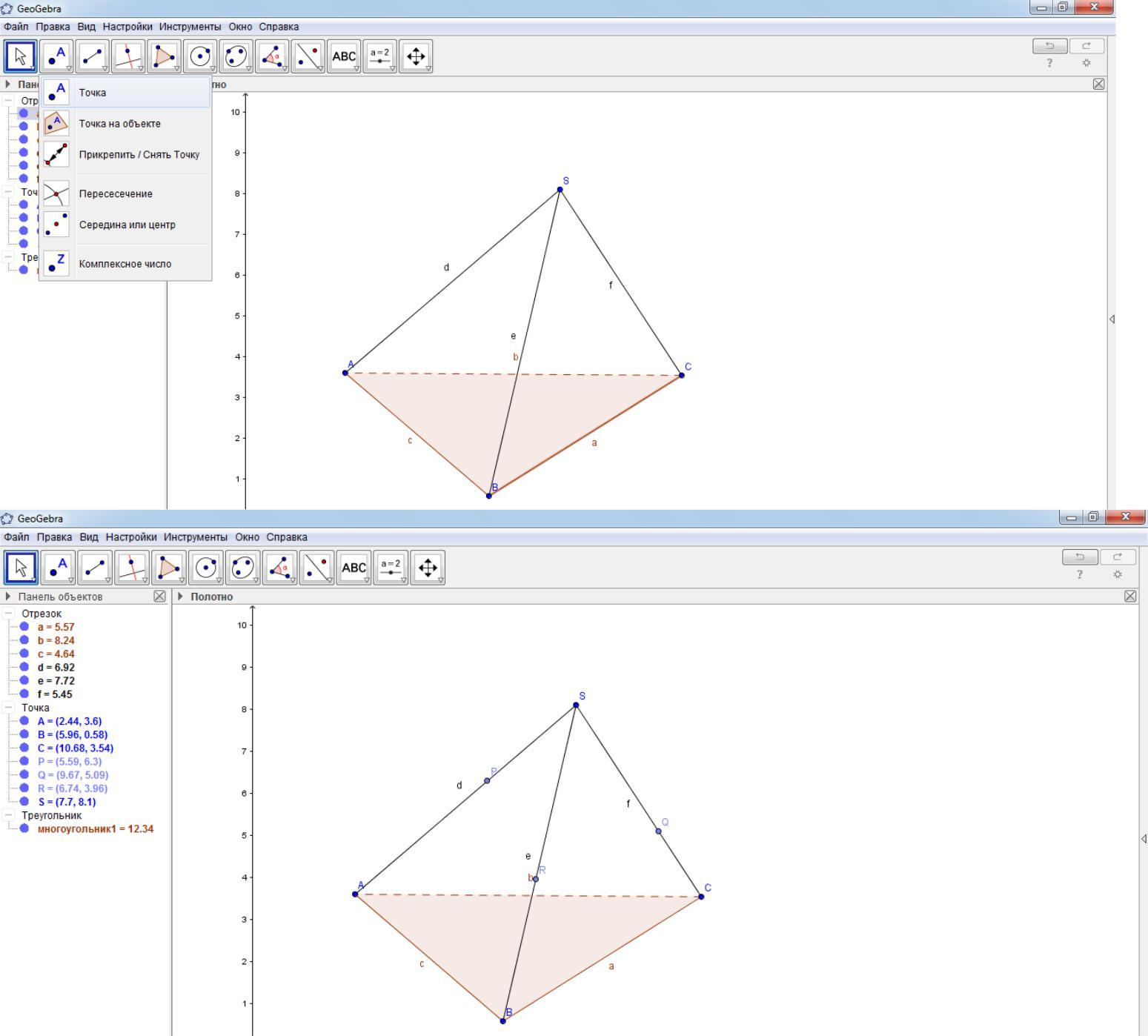
1. С помощью инструмента «Прямая» по двум точкам построить прямые PR, PQ, RQ с помощью щелчков левой кнопки мыши в данных точках.

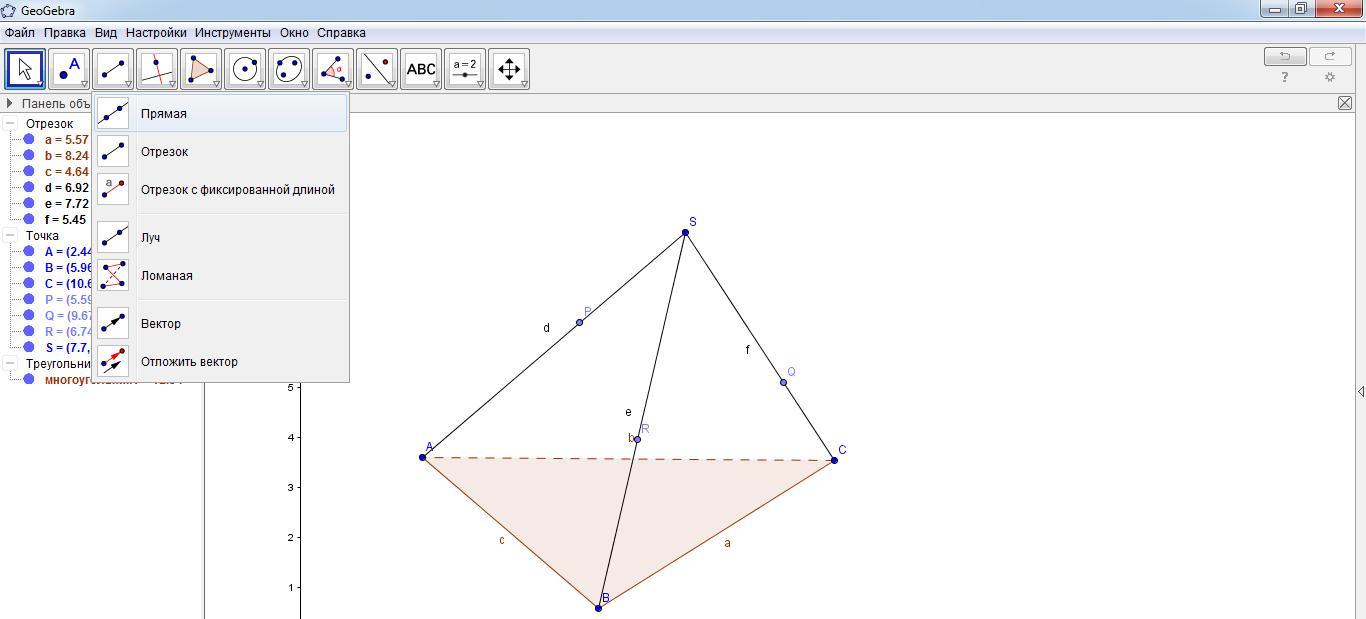
1. Выбрать инструмент «Многоугольник» и щелкнуть по очереди по точкам PQRP.

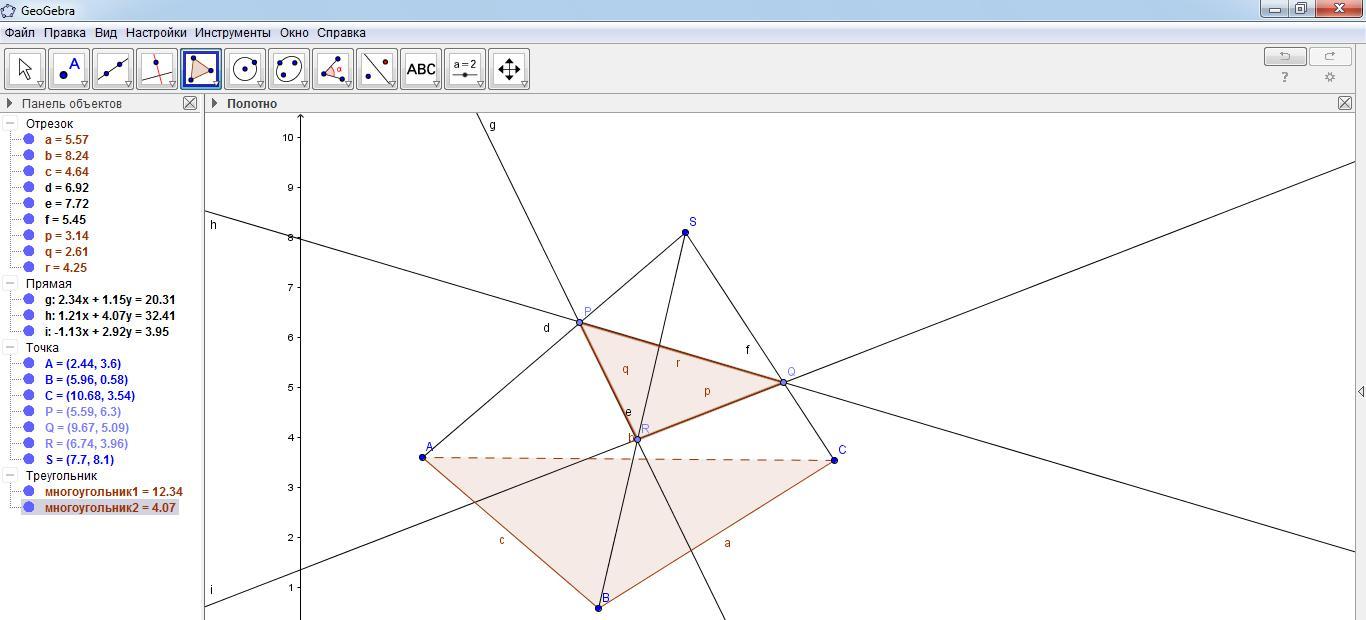
1. П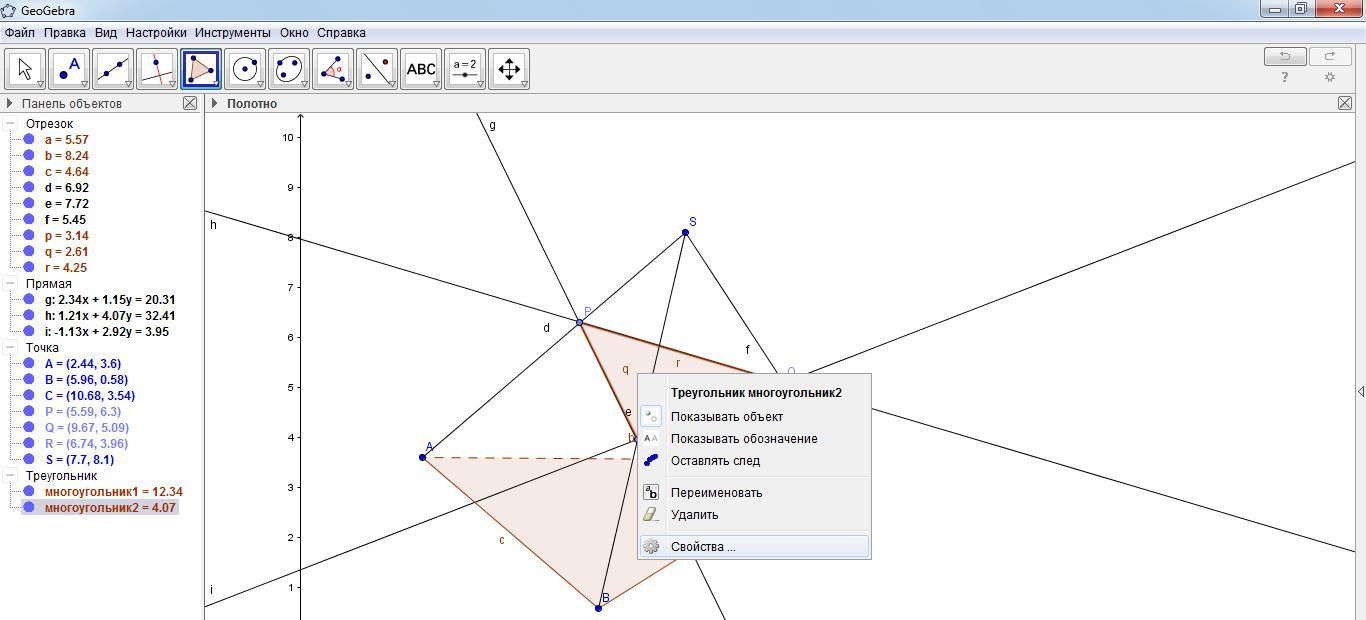 остроенный многоугольник является сечением пирамиды плоскостью, проходящей через точки P,Q,R. В сечении получился треугольник PQR. Щелкнуть по треугольнику правой кнопки мыши и выбрать свойства – цвет. Заливаем треугольник каким-нибудь цветом.

1. Н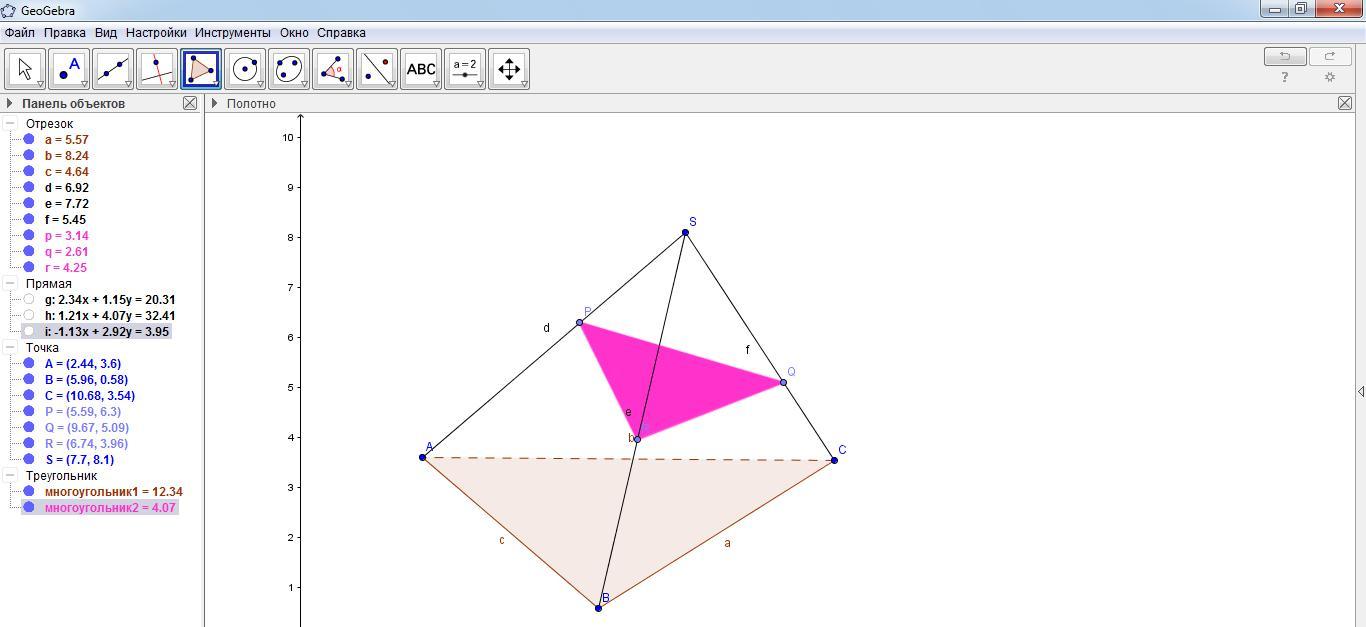 а панели объектов щелкнуть по маркерам (по кружочкам), определяющим прямые g, h, i для того, чтобы скрыть прямые, как показано на рисунке.

1. С помощью инструмента «Перемещать» меняем положение точек P, Q, R и следим за изменениями сечения.

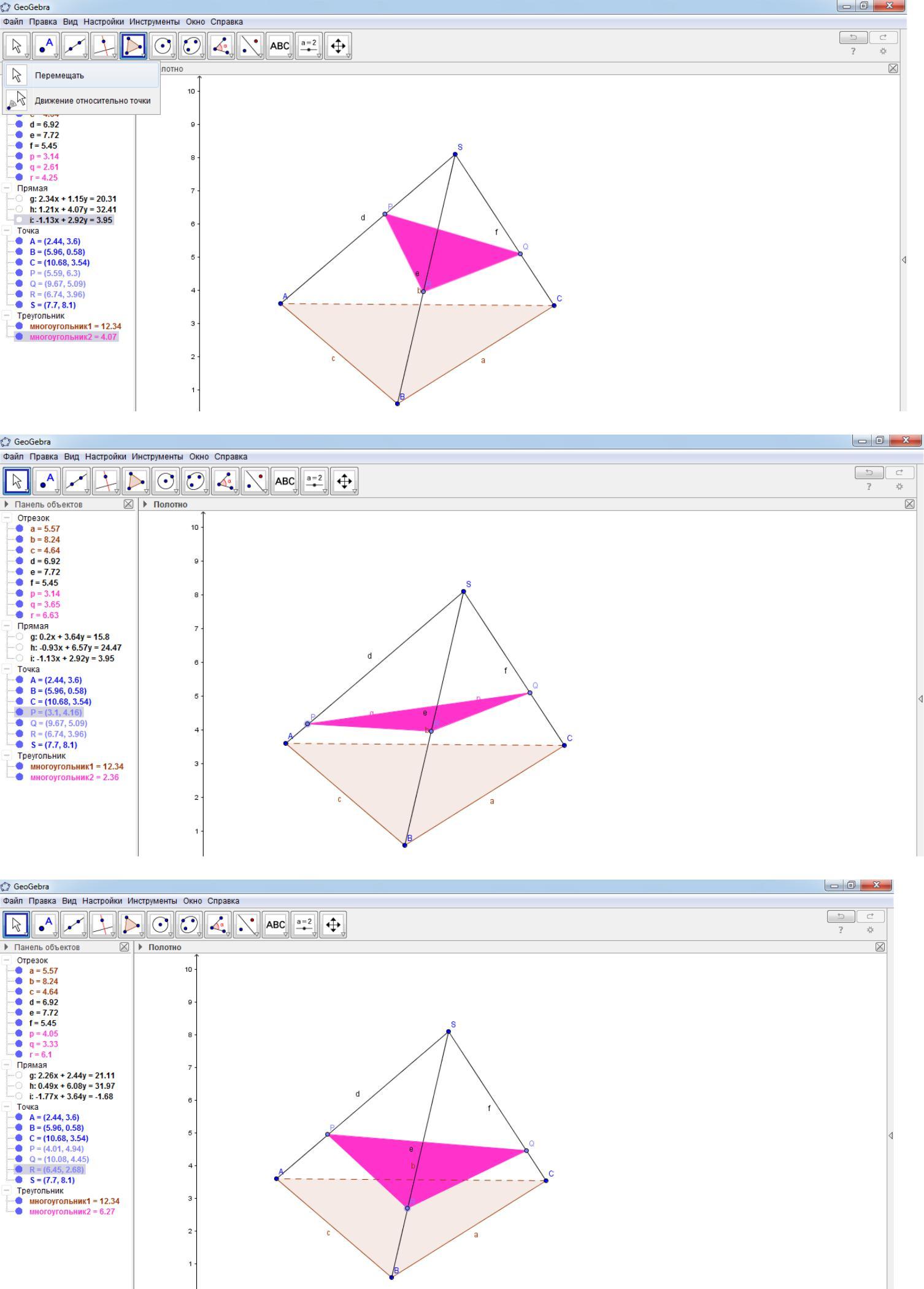
1. В качестве дополнительного задания можно измерить площадь сечения. Для этого выбрать инструмент «Площадь» и щелкнуть левой кнопкой мыши по многоугольнику PQR.

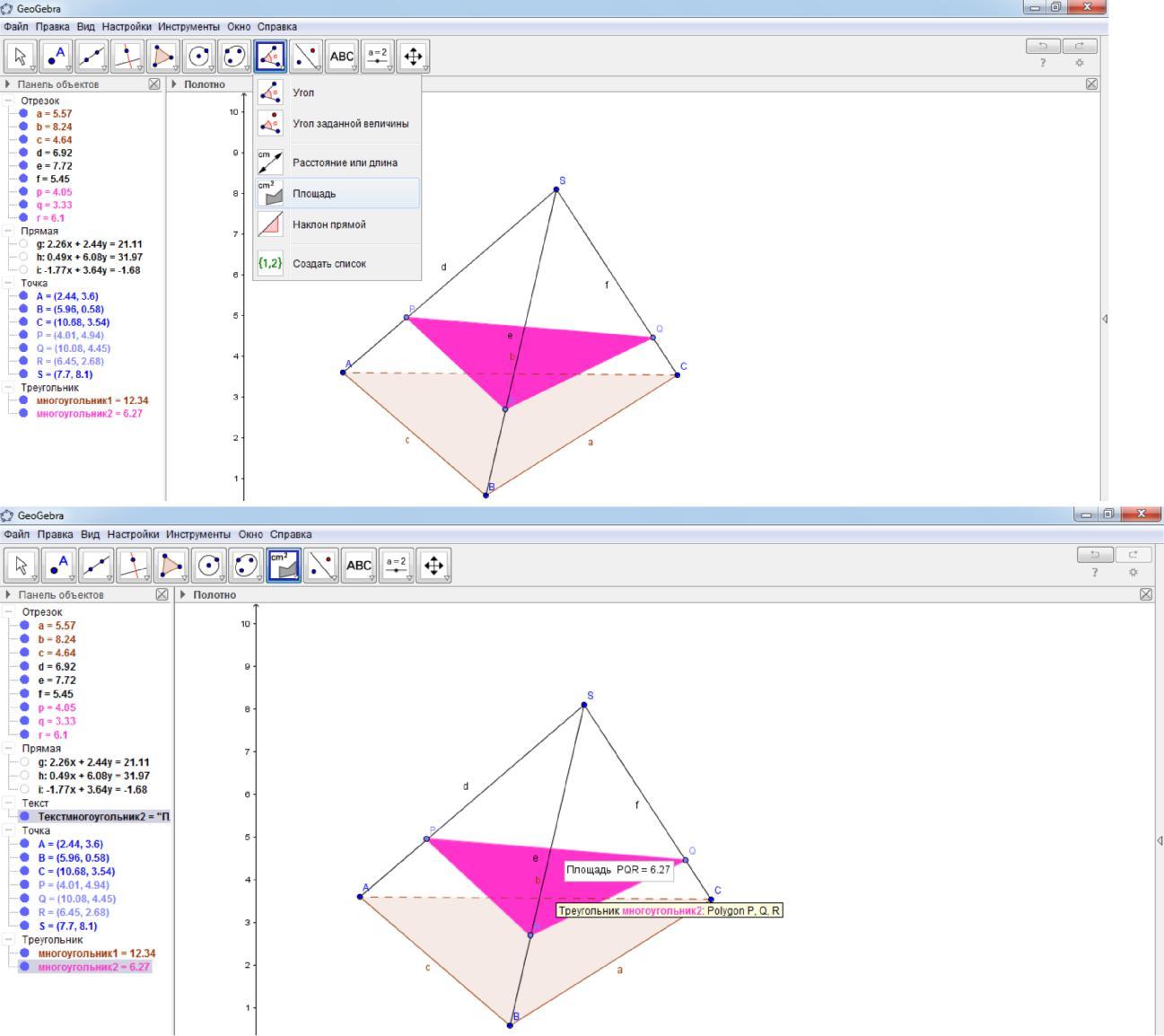
Задача 75. (повышенной сложности) Построить сечение пирамиды SABC плоскостью PQR, если точка P лежит на прямой SA (точнее на продолжении луча SA), точка Q лежит на ребре SB, точка R лежит на ребре SC.

Решение (построение):

1. С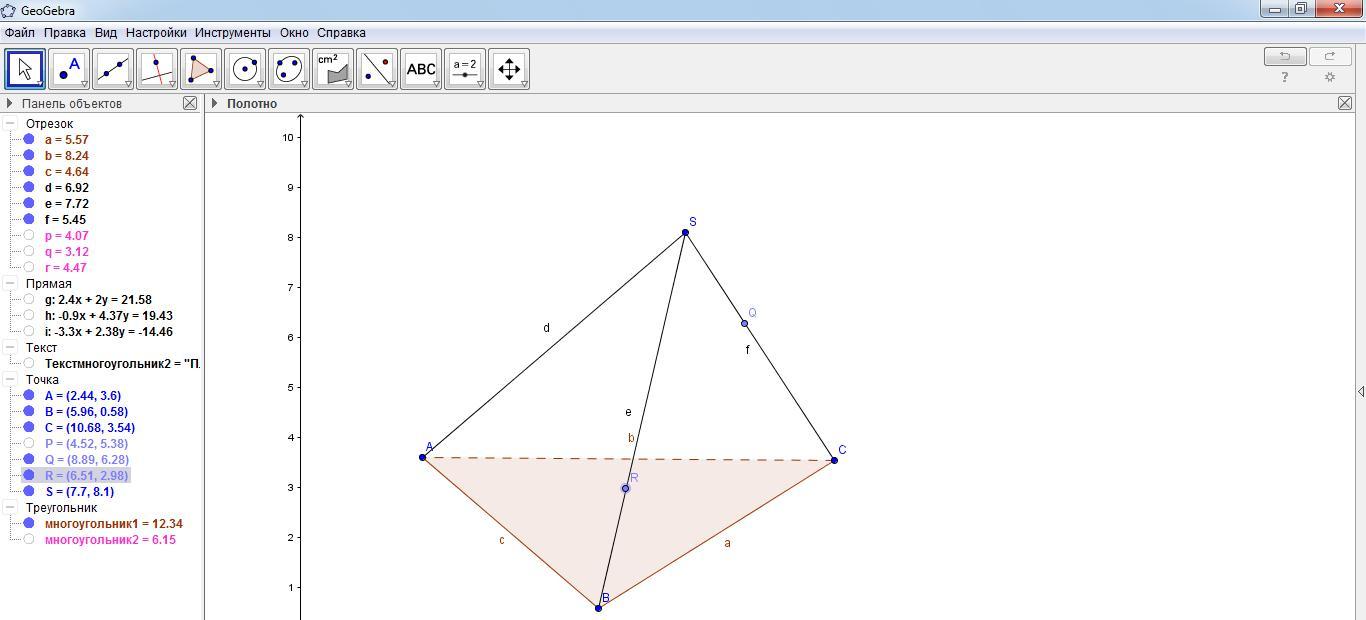 крыть объекты многоугольник 2 (треугольник сечения), текст многоугольника (вычисленная площадь сечения) и точку P. Поменять положение точек Q и R как показано на рисунке.

1. С помощью инструмента «Прямая» построить прямую SA.

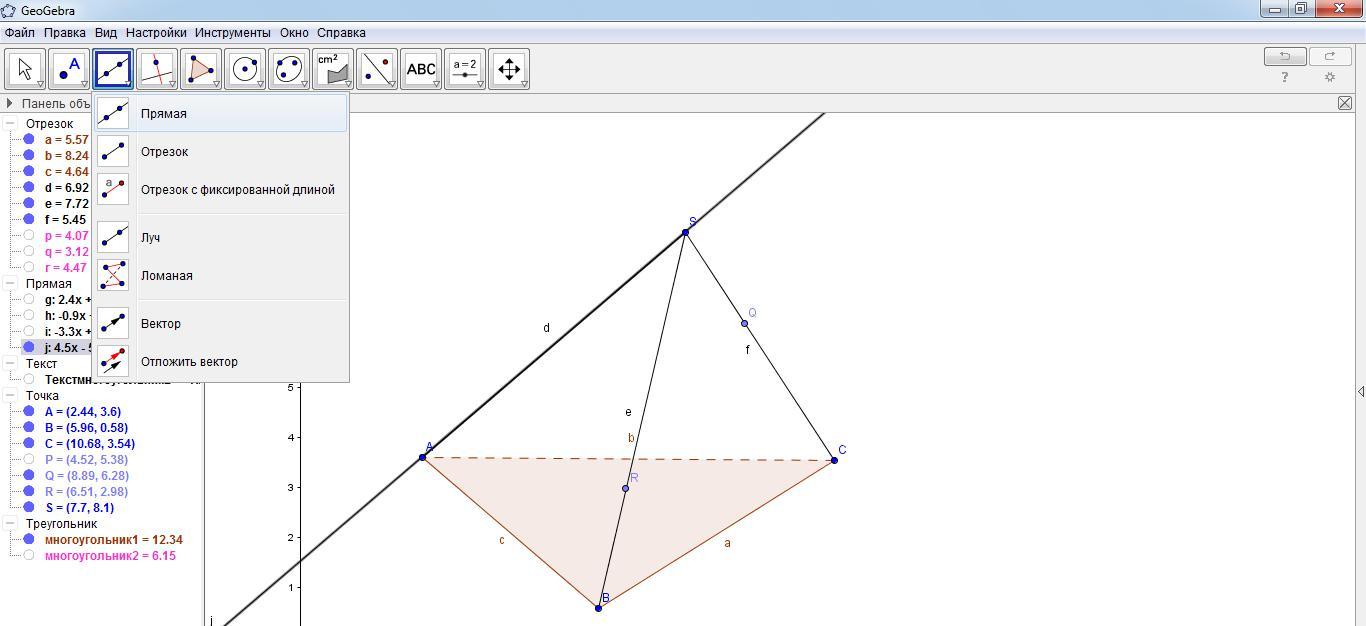
1. На прямой SA отметить точку P₁ с помощью инструмента «Точка», как показано на рисунке (на продолжении луча SA).

1. Провести прямую P₁ R.

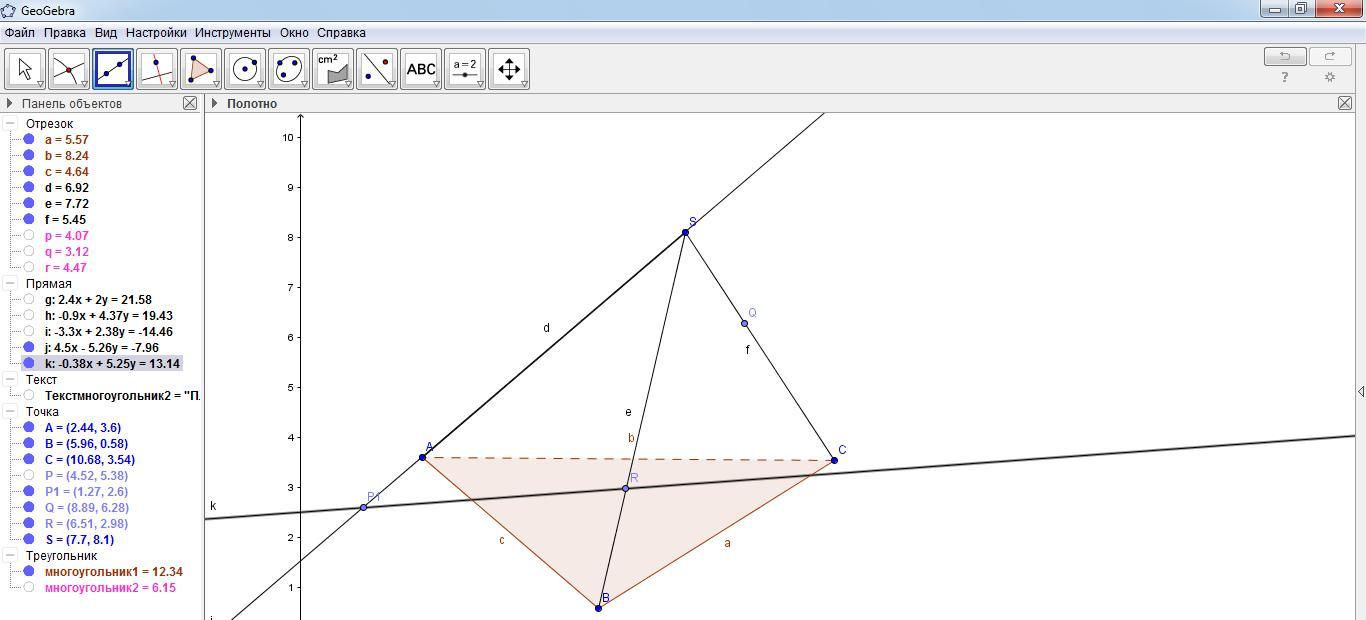
1. П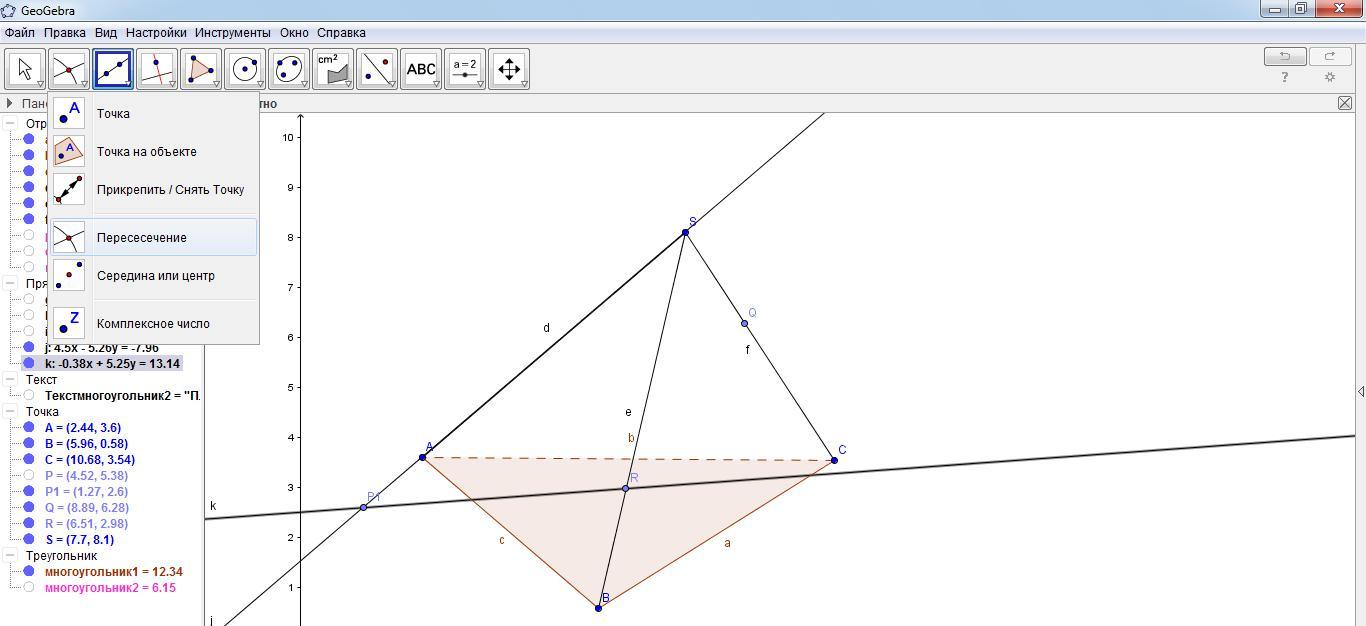 рямые AB и P₁R лежат в плоскости грани SAB. Найдем их точку пересечения K. Для этого выбрать инструмент «Пересечение» двух объектов и щелкнуть левой кнопкой мыши по прямым AB и P₁ R.

1. Провести прямую P₁ Q.

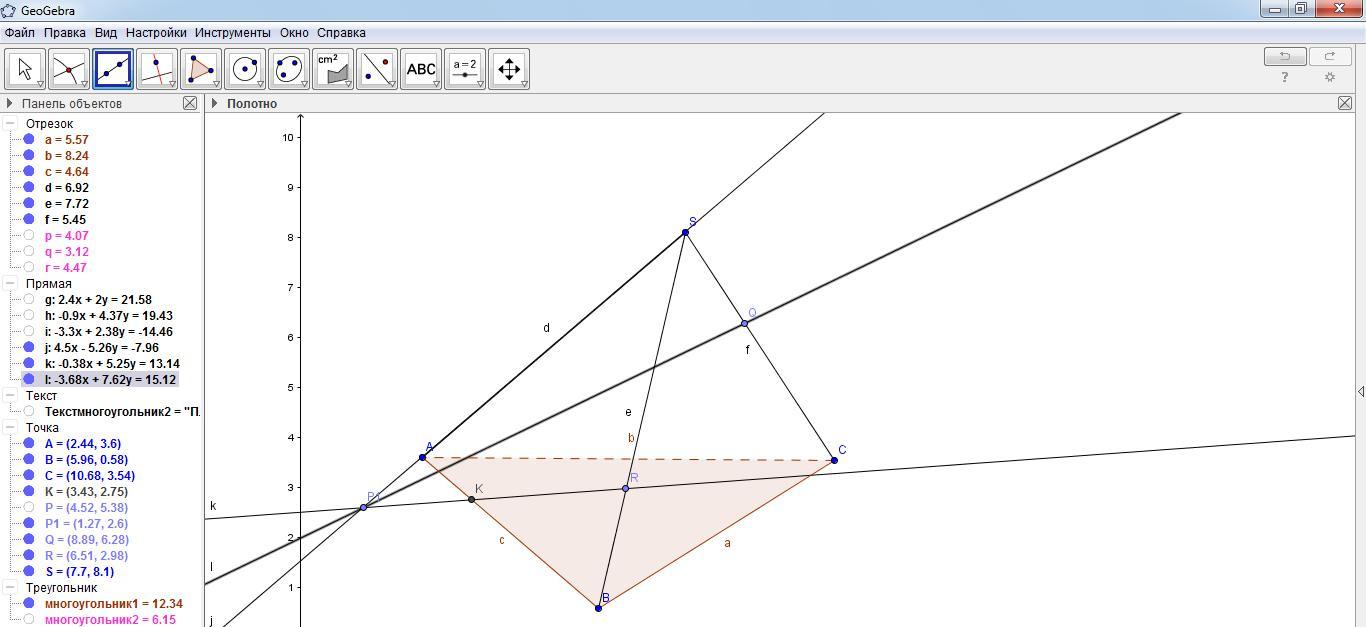
1. Прямые AС и P₁Q лежат в плоскости грани SAC. Найдем их точку пересечения M. Для этого выбрать инструмент «Пересечение» двух объектов и щелкнуть левой кнопкой мыши по прямым AC и P₁Q.

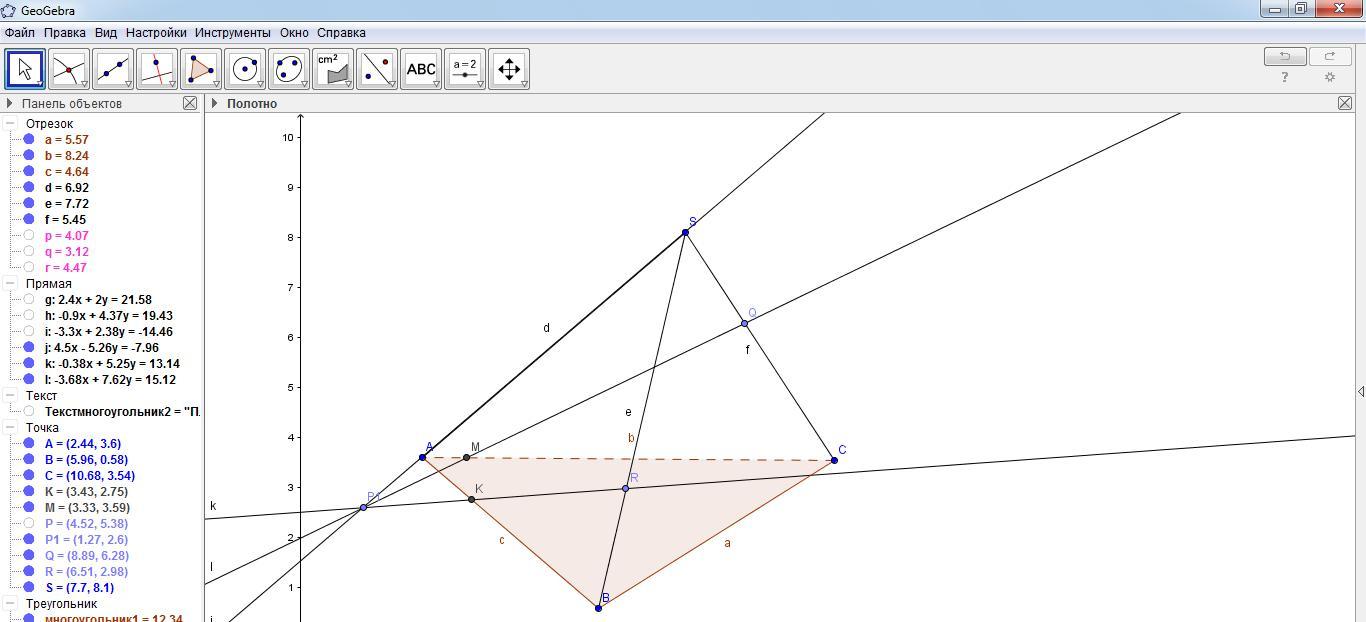
1. Через две пересекающиеся прямые P₁R и P₁Q проходит единственная плоскость и это и есть плоскость сечения. Проведем прямые MK и QR. Прямая MK – это прямая, по которой пересекаются плоскость сечения и плоскость основания пирамиды.

1. Построить многоугольник QRKMQ. Построенный многоугольник является сечением пирамиды плоскостью, проходящей через точки P1,Q,R. В сечении получился четырехугольник QRKM.

1. Залить каким-нибудь цветом и скрыть вспомогательные прямые, как показано на рисунке.

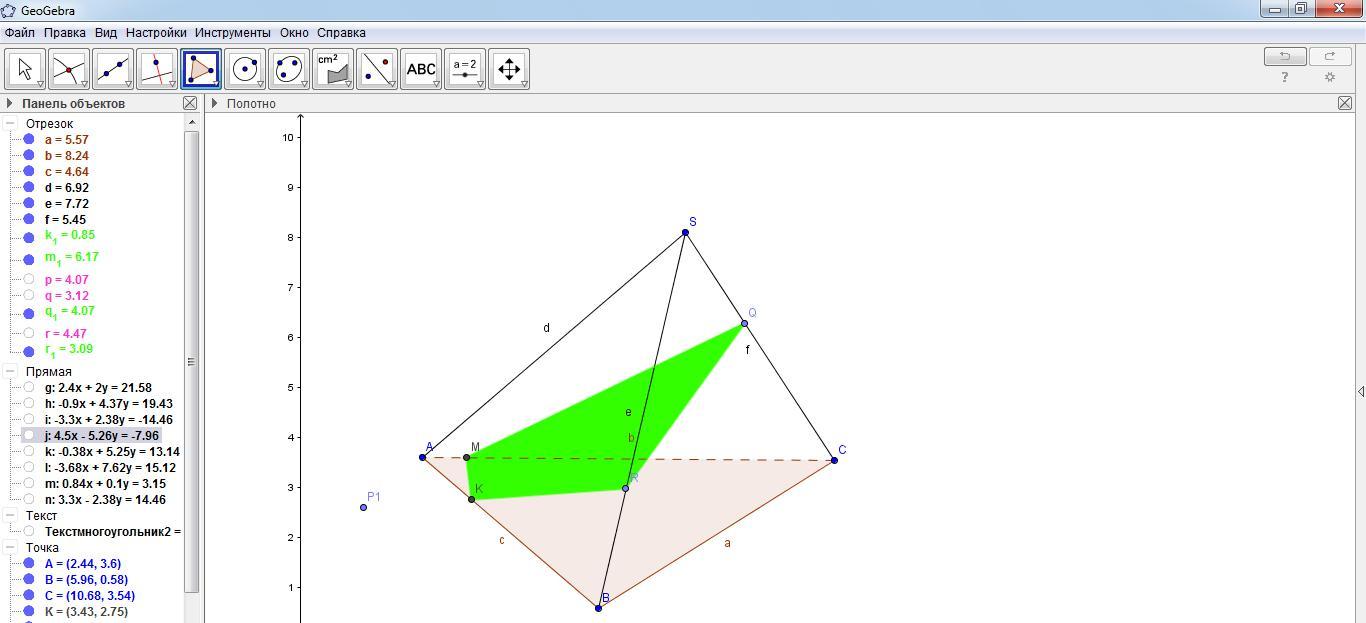
1. С помощью инструмента «Перемещать» двигаем точку P₁ вдоль прямой SA и рассматриваем различные положения плоскости сечения.

ф

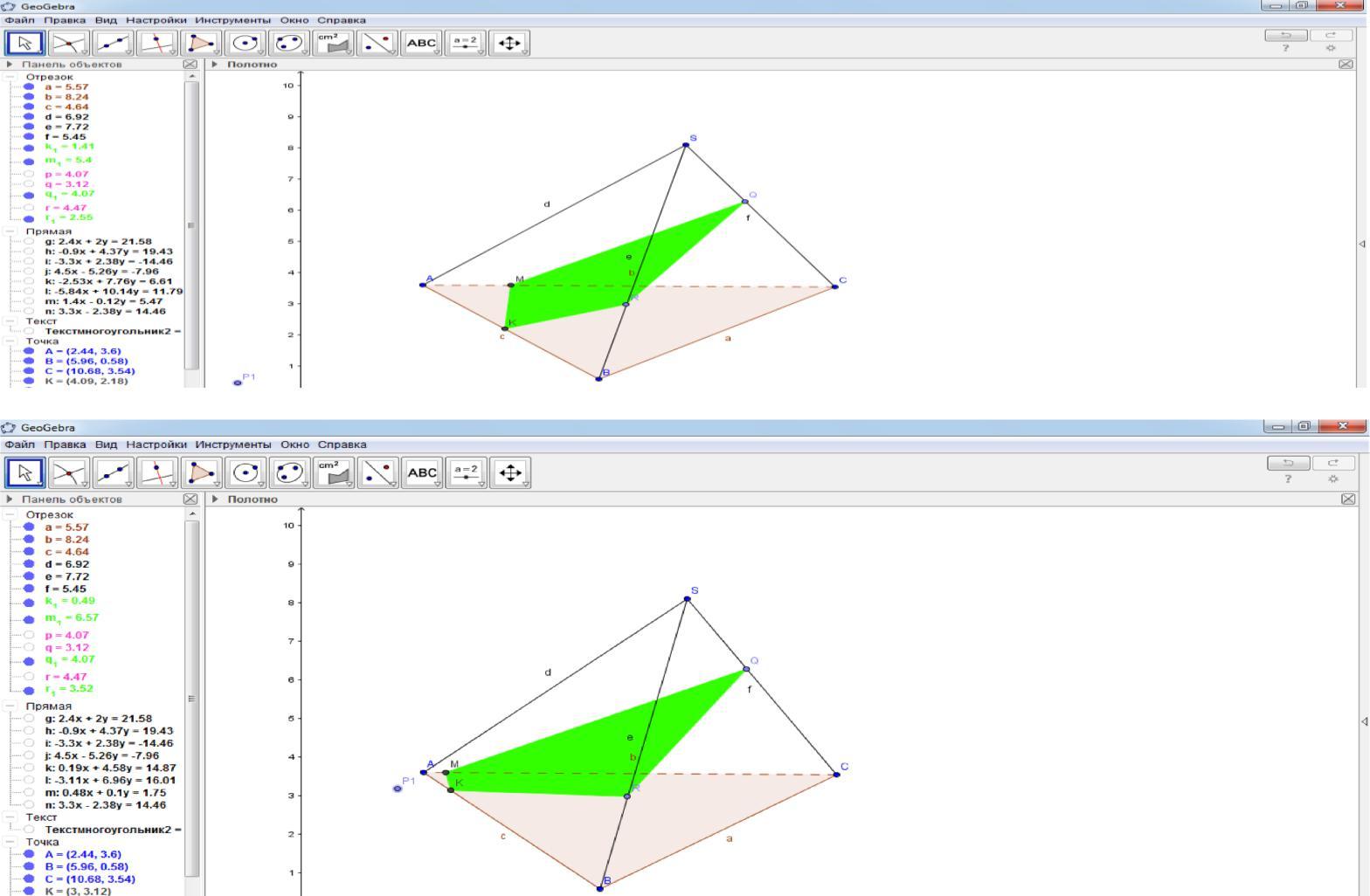
Теперь выполним самостоятельное решение задач по вариантам.

Вариант 1.

Задача 80. Построить сечение прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, определяемое параллельными прямыми АА₁ и СС₁. Сколько плоскостей проходит через параллельные прямые?

Решение (построение): Через две параллельные прямые проходит плоскость и притом только одна. Построение оформить самостоятельно. Файл сохранить в своей папке под именем задача 80.

Ответ:

Задача 104. Построить сечение треугольной призмы ABCA₁B₁C₁ плоскостью, проходящей через ребро AC и середину ребра B₁C₁. При построении сечения использовать свойство параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны).

Решение (построение): Подсказка: использовать инструмент Середина или центр для того, чтобы построить середину отрезка B₁C₁ (после выбора этого инструмента щелкнуть левой кнопкой мыши по точкам B₁ и C₁, середина определится автоматически программой) и использовать инструмент «Параллельная прямая» и щелкнуть по прямой AC и точке M (параллельные плоскости ABC и A₁B₁C₁ пересечены плоскостью сечения, а значит линии пересечения параллельны). Не забудьте использовать инструмент «Пересечение двух объектов». Построение оформить самостоятельно. Файл сохранить в своей папке под именем задача 104.

Ответ:

Вариант 2.

Задача 81. Построить сечение прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, определяемое пересекающимися прямыми А₁С и АС₁. Сколько плоскостей проходит через пересекающиеся прямые?

Решение (построение): Через две пересекающиеся прямые проходит плоскость и притом только одна. Построение оформить самостоятельно. Файл сохранить в своей папке под именем задача 81.

Ответ:

Задача 105. Построить сечение четырехугольной пирамиды SABCD плоскостью, проходящей через точку K параллельно плоскости основания пирамиды. При построении сечения использовать свойство параллельных плоскостей (если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны).

Решение (построение): Подсказка: использовать инструмент «Параллельная прямая» и щелкнуть по прямой DC и точке K (параллельные плоскости ABCD и плоскость сечения пересечены плоскостью SDC, а значит, линии пересечения параллельны) и далее двигаться аналогично по граням сначала SAD, а затем SAB. Не забудьте использовать инструмент Пересечение двух объектов, по очереди получите новые точки M, N, L. Построение оформить самостоятельно. Файл сохранить в своей папке под именем задача 105.

Ответ: