Условная вероятность. Правило умножения вероятностей. Формула полной вероятности. Формула Байеса.

Условная вероятность. Правило умножения вероятностей. Формула полной вероятности. Формула Байеса.

Презентация по математике преподавателя « Орского технического техникума имени А. И. Стеценко » филиал пос. Энергетик Николаевой Натальи Юрьевны Оренбургская область Новоорский район посёлок Энергетик.

Условная вероятность

• Вероятность события  A  при условии того, что событие  B  произошло, называется  условной  вероятностью и обозначается 

или

Пример 1.

Пусть пять студентов вытягивают на экзамене один билет из пяти, причем один из них - очень лёгкий. Какова вероятность для того, кто идёт третьим, вытащить удачный билет?

Решение.

Очевидно, что эта вероятность зависит от того, что попалось предыдущим студентам , и вытянуть удачный билет третий студент может только в том случае, когда его не взяли двое предыдущих:

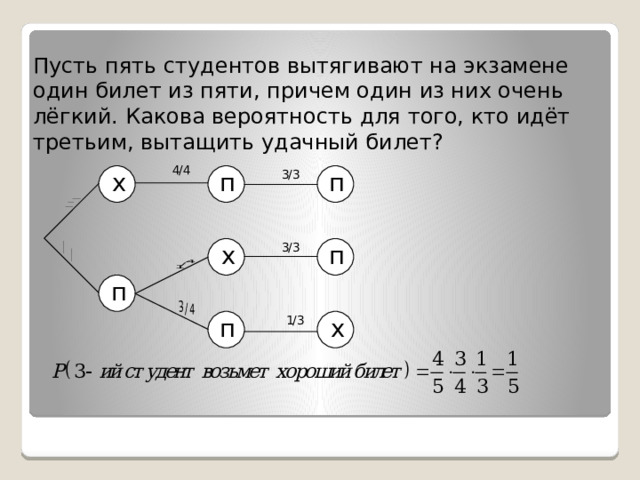
Пусть пять студентов вытягивают на экзамене один билет из пяти, причем один из них очень лёгкий. Какова вероятность для того, кто идёт третьим, вытащить удачный билет?

Теорема умножения для

независимых событий

Вероятность произведения двух

независимых событий А и В равна

произведению их вероятностей.

ЗАДАЧА Если гроссмейстер А. играет белыми,

то он выигрывает у гроссмейстера Б. с вероятностью

0,52. Если А. играет черными, то А. выигрывает у Б.

с вероятностью 0,3. Гроссмейстеры А. и Б. играют две

партии, причем во второй партии меняют цвет фигур.

Найдите вероятность того, что А. выиграет оба раза.

Решение.

Обозначим С=;

D=

р(С)=0,52; р(D)=0,3; события независимы;

ОТВЕТ: 0,156

Формула полной вероятности

Для вычисления полной вероятности события A нужно перечислить все условия Hi, при которых может наступить A, и перемножить вероятности этих условий на соответствующие им условные вероятности.

Причем сумма вероятностей гипотез должна быть равна 1, т.е.

Пусть событие A может быть вызвано набором причин Hi. Тогда вероятность того, что к событию A привело событие Hi, пропорциональна произведению вероятности соответствующей причины на вероятность следствия.

Формула Байеса

Пример 2.

Имеются 2 урны с шарами. В первой урне находятся 2 белых и 4 черных шара, во второй – 3 белых и 3 черных.

• Из каждой урны достали по одному шару. Найти вероятность того, что эти шары белые.
• Выбирается урна и из нее извлекается 2 шара. Найти вероятность того, что эти шары белые. Найти вероятность того, что они были взяты из первой урны.
• Из первой урны во вторую переложили 1 шар, а затем из второй (пополненной) урны достали 2 шара. Они оказались белыми. Найти вероятность того, что был переложен белый шар.

3/5

3/6

2/5

3/6

3/6

3/6

Пример 2.1

Имеются 2 урны с шарами. В первой урне находятся 2 белых и 3 черных шара, во второй – 3 белых и 3 черных. Из каждой урны достали по одному шару. Найти вероятность того, что эти шары белые.

Из I урны

Из II урны

1/2

1/2

3/6

3/6

3/5

1/4

2/5

2/4

2/4

2/5

3/5

2/5

3/4

Пример 2.2

Имеются 2 урны с шарами. В первой урне находятся 2 белых и 3 черных шара, во второй – 3 белых и 3 черных. Выбирается урна и из нее извлекается 2 шара. Найти вероятность того, что эти шары белые. Найти вероятность того, что они были взяты из первой урны.

3/5

2/6

4/6

4/7

3/7

3/7

4/7

3/6

3/6

4/6

2/6

2/6

4/6

3/6

3/6

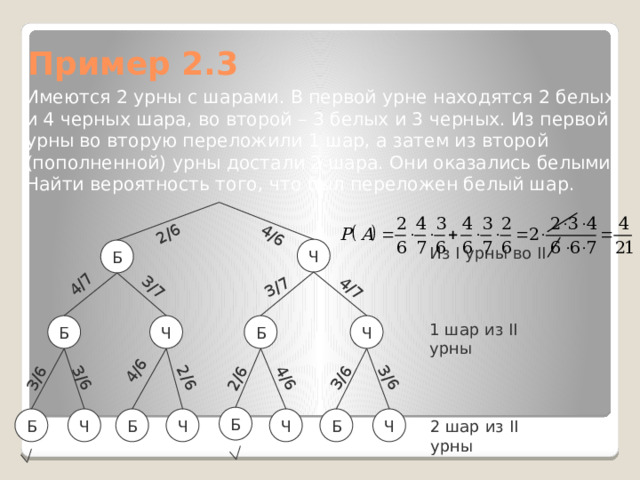
Пример 2.3

Имеются 2 урны с шарами. В первой урне находятся 2 белых и 4 черных шара, во второй – 3 белых и 3 черных. Из первой урны во вторую переложили 1 шар, а затем из второй (пополненной) урны достали 2 шара. Они оказались белыми. Найти вероятность того, что был переложен белый шар.

Из I урны во II

Ч

Б

1 шар из II урны

Б

Ч

Б

Ч

Б

Б

Ч

Б

Ч

Б

Ч

Ч

2 шар из II урны

1/3

1/3

1/3

1/3

1/3

1/3

1/3

1/2

1/3

1/3

1/3

1/3

1/3

1

1/2

1

1

1/2

1/2

1/2

1/2

1

1

1

Дерево исходов

Меняет выбор и выигрывает

Не меняет выбор и выигрывает

C

B

A

Ваш выбор

A

A

C

C

B

A

C

B

B

B

B

C

C

A

C

C

A

A

B

A

B

Формула Байеса

Рассмотрим событие А, которое может наступить лишь при появления одного из несовместных событий В 1 , В 2 , В 3 ,…,В n , образующих полную группу. Если событие А уже произошло, то вероятность событий В 1 , В 2 , В 3 ,…,В n можно определить по формуле Байеса

Задача 1

• Два автомата производят одинаковые детали. Производительность первого автомата в два раза больше производительности второго. Вероятность производства отличной детали у первого автомата равна 0,60, а у второго 0,84. Наудачу взятая для проверки деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.

Решение

• Событие А - деталь отличного качества.

Гипотезы:

• В 1  – деталь произведена первым автоматом,   ,

так как этот автомат производит деталей в два раза больше второго.

• В 2  – деталь изготовлена вторым автоматом,
• Условные вероятности того, что деталь произведена первым автоматом,  

а вторым

Вероятность того, что наудачу взятая деталь окажется отличного качества, вычисляем по формуле полной вероятности:

.

Решение

• Вероятность того, что взятая деталь изготовлена первым автоматом, вычисляется по формуле Байеса: 

Задача 2

• Число грузовых машин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе, как 4:1. Вероятность того, что будет заправляться грузовая машина, равна 0,2; для легковой машины эта вероятность равна 0,3. К бензоколонке подъезжала для заправки машина. Найти вероятность того, что эта машина грузовая

Решение

• Cобытие A - машина заехала на заправку.

Гипотезы: H1 - это грузовая машина,

H2 - это легковая машина,

• Условные вероятности:
• По формуле полной вероятности вероятность того, что случайным образом выбранная из общего потока машина зарулит на бензоколонку

• Искомую вероятность найдём по формуле Байеса

• Ответ: 0,727

Задача 3

• Три студентки живут в одной комнате и по очереди моют посуду. Вероятность разбить тарелку для первой студентки равна 0.03, для второй 0.01, для третьей - 0.04. На кухне раздался звон разбитой тарелки. Найти вероятность того, что третья студентка мыла тарелку.

• Событие A - разбили тарелку.
• Гипотезы:

H1 - тарелку разбила 1-я студентка, P(H1)=0,03

H2 - тарелку разбила 2-я студентка, P(H2)=0,01

H3 - тарелку разбила 3-я студентка, P(H3)=0,04

(гипотезы Н1,Н2,Н3 составляют полную группу событий)

• Условные вероятности (кто мыл посуду в момент катастрофы):

Решение

Решение

• По формуле полной вероятности вероятность того, что в процессе мытья посуды будет разбита тарелка

• Искомую вероятность найдём по формуле Байеса (переоценка вероятности события H3

• Ответ: 0,5

Полная группа событий

• в результате данного испытания обязательно появится хотя бы одно из них.

Теорема

Если событие А может произойти только вместе с одной из гипотез Н 1 , Н 2 …Н n , образующих полную группу попарно несовместных событий, то вероятность события А

Р(А) = Р(Н 1 )Р Н1 (А) + Р(Н 2 )Р Н2 (А) + … + +Р(Н n )P Hn (A)

Формула полной вероятности

Пример

В цехе работают 20 станков.

Из них 10 марки А, 6 марки В, и 4 марки С.

Вероятности того, что деталь будет без брака для этих станков соответственно равны 0,9 , 0,8 и 0,7 .

Какова вероятность того, что наугад выбранная деталь будет браком?

Пример

События

А = «Наугад выбранная деталь будет с браком»

Н1 = «Деталь обработана на станке марки А»

Н2 = «Деталь обработана на станке марки В»

Н3 = «Деталь обработана на станке марки С»

Пример

Всего в цехе 20 станков

Р(Н 1 ) = 10/20 = ½=0,5

Р(Н 2 ) = 6/20 = 3/10 = 0,3

Р(Н 3 ) = 4/20 = 1/5 = 0,2

Условные вероятности

P Н1 (А) = 1 – 0,9 = 0,1

P Н2 (А) = 1 – 0,8 = 0,2

P Н3 (А) = 1 – 0,7 = 0,3

Пример

По формуле полной вероятности

Р(А) = Р(Н 1 )·P Н1 (А) +

+ Р(Н 2 ) ·P Н2 (А) +

+ Р(Н 3 ) ·P Н3 (А) =

= 0,5·0,1 + 0,3·0,2 + 0,2·0,3 =

= 0,05 + 0,06 + 0,06 = 0,17

Теорема

Если событие А может произойти только вместе с одной из гипотез Н 1 , Н 2 …Н n , образующих полную группу попарно несовместных событий, то вероятность гипотез после испытания, когда событие А уже имело место

Р A (Н i ) = Р(Н i )Р Нi (А) /Р(A)

Формула Байеса

Пример

В цехе работают 20 станков.

Из них 10 марки А, 6 марки В, и 4 марки С. Вероятность того, что деталь будет без брака для этих станков соответственно равны 0,9 , 0,8 и 0,7 .

Наугад выбрали деталь. Она оказалась с браком.

Какова вероятность того, что она была изготовлена на станке марки В?

Пример

События

А = «Наугад выбранная деталь будет с браком»

Н1 = «Деталь обработана на станке марки А»

Н2 = «Деталь обработана на станке марки В»

Н3 = «Деталь обработана на станке марки С»

Пример

Р(Н 2 ) = 0,3

P Н 2 (А) = 0,2

Р(А) = 0,17

По формуле Байеса

Р A (Н 2 ) = Р(Н 2 ) · Р Н 2 (А) / Р(A) =

= 0,3· 0,2 / 0,17 = 0,06 / 0,17 =

= 0,35

Пример

По формуле Байеса

Р A (Н 2 ) = Р(A) / (Р(Н 2 )Р Н2 (А)) =

Р(А) = Р(Н 1 )·P Н1 (А) +

+ Р(Н 2 ) ·P Н2 (А) +

+ Р(Н 3 ) ·P Н3 (А) =

= 0,5·0,1 + 0,3·0,2 + 0,2·0,3 =

= 0,05 + 0,06 + 0,06 = 0,17