При выполнении заданий 2, 3, 8, 14 выберите один из четырёх предлагаемых вариантов ответа. Ответом на задания 1, 4—7, 9—13, 15—20 является целое число или конечная десятичная дробь. Дробную часть от целой отделяйте запятой. Единицы измерений писать не нужно.
Вариант №3
1. Вычислите: 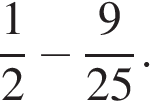
2. На координатной прямой отмечены числа a и x.

Какое из следующих чисел наименьшее?
В ответе укажите номер правильного варианта.
1) 
2) 
3) 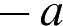
4) 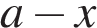
3. Сравните числа  и 16.
и 16.
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4. Решите уравнение 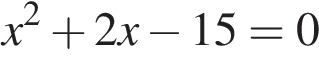 .
.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Задание 4 № 311439
Решение.
По теореме, обратной теореме Виета — сумма корней равна −2, а их произведение равно −15. Тем самым, это числа −5 и 3.
Ответ: −5; 3.
Ответ: -5; 3
5. На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
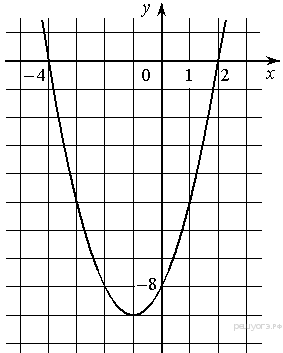
1) f( −2) = f(2)
2) f(x)0 при xx2
3) Наименьшее значение функции равно −9
6. Последовательность задана формулой 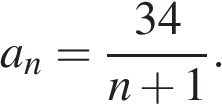 Сколько членов в этой последовательности больше 6?
Сколько членов в этой последовательности больше 6?
7. Упростите выражение 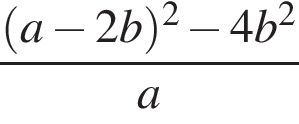 и найдите его значение при
и найдите его значение при 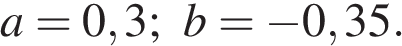
8. Решите неравенство 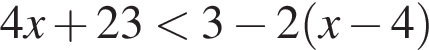 и определите, на каком рисунке изображено множество его решений.
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
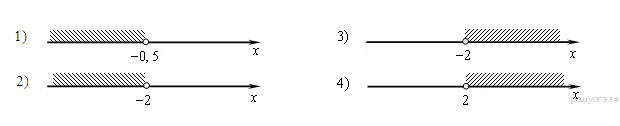
1)
2)
3)
4)
9. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 80°, угол CAD равен 54°. Найдите угол ABD. Ответ дайте в градусах.
10. 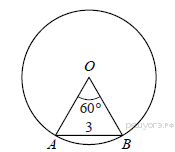 Центральный угол AOB, равный 60°, опирается на хорду АВдлиной 3. Найдите радиус окружности.
Центральный угол AOB, равный 60°, опирается на хорду АВдлиной 3. Найдите радиус окружности.
11. В ромбе сторона равна 10, одна из диагоналей — 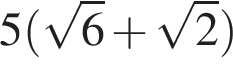 , а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
, а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
12. 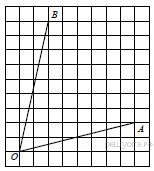 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
13. Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
2) Любые две прямые имеют не менее одной общей точки.
3) Через любую точку проходит более одной прямой.
4) Любые три прямые имеют не менее одной общей точки.
Если утверждений несколько, запишите их номера в порядке возрастания.
14. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.
| Мощность автомобиля (в л. с.) | Налоговая ставка (в руб. за л. с. в год) |
| не более 70 | 0 |
| 71—100 | 12 |
| 101—125 | 25 |
| 126—150 | 35 |
| 151—175 | 45 |
| 176—200 | 50 |
| 201—225 | 65 |
| 226—250 | 75 |
| свыше 250 | 150 |
Сколько рублей должен заплатить владелец автомобиля мощностью 219 л. с. в качестве налога за один год?
В ответе укажите номер правильного варианта.
1) 14 235
2) 75
3) 65
4) 16 425
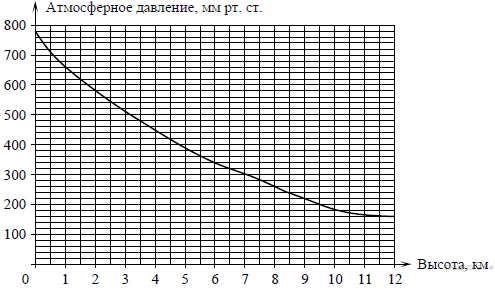
15. На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Определите по графику, на какой высоте атмосферное давление равно 260 мм рт. ст. Ответ дайте в километрах.
16. Туристическая фирма организует трехдневные автобусные экскурсии. Стоимость экскурсии для одного человека составляет 3500 р. Группам предоставляются скидки: группе от 3 до 10 человек — 5%, группе более 10 человек — 10%. Сколько заплатит за экскурсию группа из 8 человек?
17. 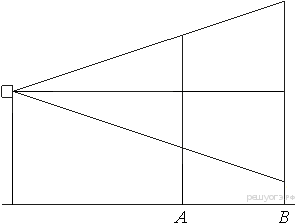 Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
18. На диаграмме показано содержание питательных веществ в какао, шоколаде, фасоли и сухарях. Определите по диаграмме, в каком продукте содержание углеводов наибольшее.

| 1) Какао | 3) Фасоль |
| 2) Шоколад | 4) Сухари |
В ответе запишите номер выбранного варианта.
19. Коля наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 3.
20. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 70 см, n =1400 ? Ответ выразите в километрах.
21. Решите неравенство 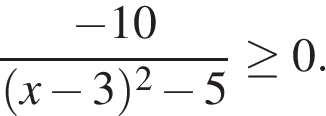
22. Теплоход проходит по течению реки до пункта назначения 76 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20 часов после отплытия из него.
23. Постройте график функции
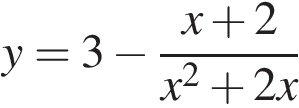
и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
24. Найдите угол АСО, если его сторона СА касается окружности, О— центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 100°.
25. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED . Докажите, что данный параллелограмм — прямоугольник.
26. Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны ACвтрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.








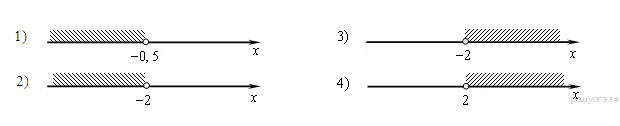
 Центральный угол AOB, равный 60°, опирается на хорду АВдлиной 3. Найдите радиус окружности.
Центральный угол AOB, равный 60°, опирается на хорду АВдлиной 3. Найдите радиус окружности. Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
 Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?










