При выполнении заданий 2, 3, 8, 14 выберите один из четырёх предлагаемых вариантов ответа. Ответом на задания 1, 4—7, 9—13, 15—20 является целое число или конечная десятичная дробь. Дробную часть от целой отделяйте запятой. Единицы измерений писать не нужно.
Вариант № 4
1. Найдите значение выражения 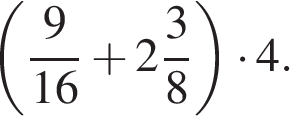
2. На координатной прямой отмечены числа a, b, и c.
В ответе укажите номер правильного варианта.

Укажите номер верного утверждения.
1) 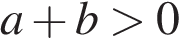
2) 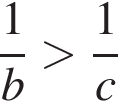
3) 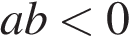
4) 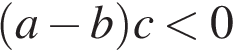
3. Площадь территории России составляет 1,7 · 107 км2, а Норвегии — 3,2⋅105 км2. Во сколько раз площадь территории России больше площади территории Норвегии?
В ответе укажите номер правильного варианта.
1) примерно в 1,9 раза
2) примерно в 5,3 раза
3) примерно в 53 раза
4) примерно в 530 раз
4. Найдите корни уравнения 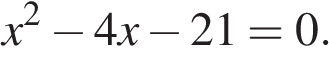
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
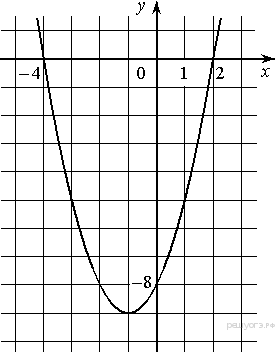
1) Функция убывает на промежутке [−1; +∞).
2) f(−3)f(0).
3) f(x)x
6. Выписаны первые несколько членов геометрической прогрессии: −175; −140; −112; ... Найдите её пятый член.
7. Найдите значение выражения 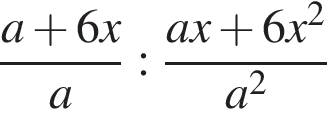 при
при 
8. Решите неравенство
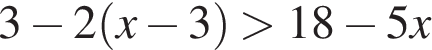
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
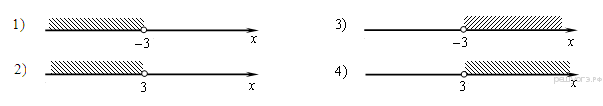
9. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
10. 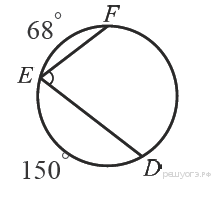 Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
11.  Найдите площадь квадрата, если его диагональ равна 3.
Найдите площадь квадрата, если его диагональ равна 3.
12. 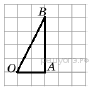 Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
13. Какое из следующих утверждений верно?
1) Диагонали параллелограмма равны.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
14. Учёный Комаров выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 8:30. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.
| Номер поезда | Отправление из Москвы | Прибытие в Санкт-Петербург |
| 032АВ | 22:50 | 05:48 |
| 026А | 23:00 | 06:30 |
| 002А | 23:55 | 07:55 |
| 004А | 23:59 | 08:00 |
Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Комарову.
В ответе укажите номер правильного варианта.
1) 032АВ
2) 026А
3) 002А
4) 004А
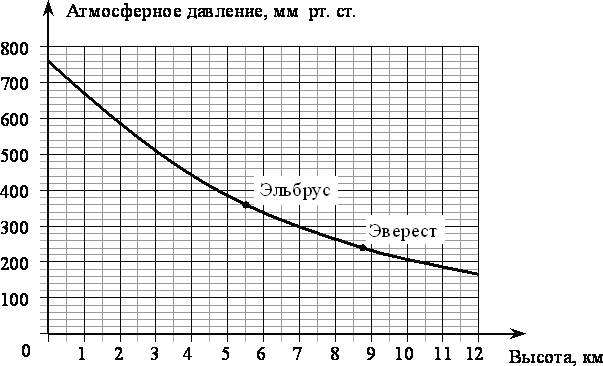
15. На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
16. Спортивный магазин проводит акцию: «Любой джемпер по цене 400 рублей. При покупке двух джемперов — скидка на второй 75%». Сколько рублей придётся заплатить за покупку двух джемперов?
17. Две трубы, диаметры которых равны 7 см и 24 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
18. 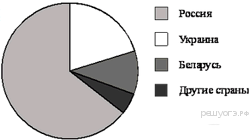 На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.
Какое из следующих утверждений неверно?
1) Пользователей из Украины больше, чем пользователей из Литвы.
2) Пользователей из Украины меньше четверти общего числа пользователей.
3) Пользователей из Беларуси больше 3 миллионов.
4) Пользователей из России больше, чем из всех остальных стран, вместе взятых.
19. В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмен из Швеции и 2 спортсмена из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что спортсмен из Швеции будет стартовать последним.
20. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 63° по шкале Фаренгейта? Ответ округлите до десятых.
21. Решите уравнение 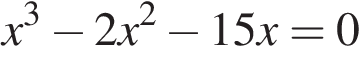
22. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
23. Постройте график функции 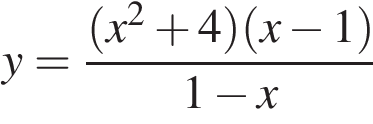 и определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
24. Стороны AC, AB, BC треугольника ABC равны 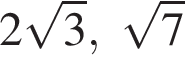 и 1 соответственно. Точка K расположена вне треугольника ABC , причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K , A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC90° .
и 1 соответственно. Точка K расположена вне треугольника ABC , причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K , A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC90° .
25. 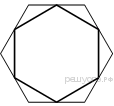 Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
26. В треугольнике 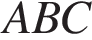 биссектриса угла
биссектриса угла 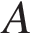 делит высоту, проведённую из вершины
делит высоту, проведённую из вершины 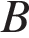 , в отношении
, в отношении 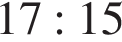 , считая от точки
, считая от точки 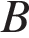 . Найдите радиус окружности, описанной около треугольника
. Найдите радиус окружности, описанной около треугольника 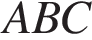 , если .
, если .








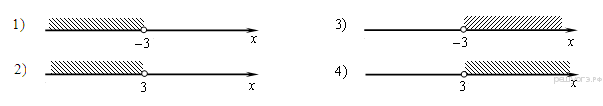
 Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно. Найдите площадь квадрата, если его диагональ равна 3.
Найдите площадь квадрата, если его диагональ равна 3. Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
 На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей. Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.









