При выполнении заданий 2, 3, 8, 14 выберите один из четырёх предлагаемых вариантов ответа. Ответом на задания 1, 4—7, 9—13, 15—20 является целое число или конечная десятичная дробь. Дробную часть от целой отделяйте запятой. Единицы измерений писать не нужно.
Вариант № 5
1. Найдите значение выражения 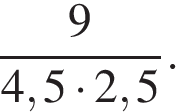
2. На координатной прямой отмечены числа a и b. Какое из следующих утверждений неверно?
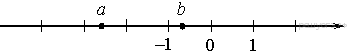
1) 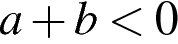
2) 
3) 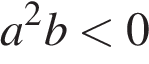
4) 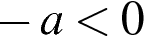
3. Найдите значение выражения 
1) 84
2) 2352
3) 
4) 252
4. Решите уравнение 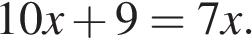
5. Упростите выражение 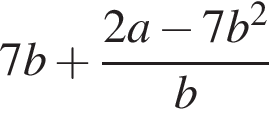 , найдите его значение при
, найдите его значение при  ;
; 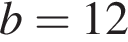 . В ответ запишите полученное число.
. В ответ запишите полученное число.
6. Геометрическая прогрессия задана условием  Найдите сумму первых её 4 членов.
Найдите сумму первых её 4 членов.
7. Сократите дробь 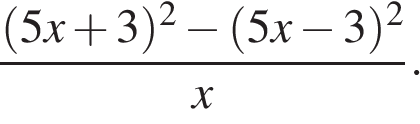
8. На каком рисунке изображено множество решений неравенства 
В ответе укажите номер правильного варианта.
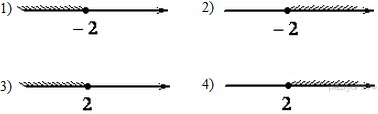
1) 1
2) 2
3) 3
4) 4
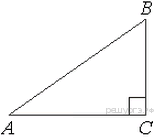 В треугольнике
В треугольнике  угол
угол  равен 90°,
равен 90°, 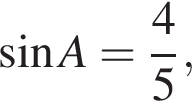
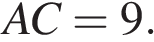 Найдите
Найдите 
10. 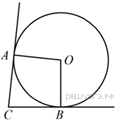 В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
11. В прямоугольном треугольнике один из катетов равен  , острый угол, прилежащий к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на
, острый угол, прилежащий к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на 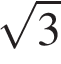 .
.
12. Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
13. Какое из следующих утверждений верно?
1) Площадь параллелограмма равна половине произведения его диагоналей.
2) Сумма углов прямоугольного треугольника равна 90 градусам.
3) Биссектрисы треугольника пересекаются в центре вписанной в него окружности.
14. В таблице даны результаты забега девочек 8 класса на дистанцию 60 м. Зачет выставляется при условии, что показан результат не хуже 10,8 с.
| Номер дорожки | I | II | III | IV |
| Время (в с) | 10,7 | 10,9 | 9,8 | 11,4 |
Укажите номера дорожек, по которым бежали девочки, не получившие зачет.
В ответе укажите номер правильного варианта.
1) только II
2) только III
3) II, IV
4) I, III
15. Из пункта A в пункт B вышел пешеход, и через некоторое время вслед за ним выехал велосипедист. На рисунке изображены графики движения пешехода и велосипедиста. На сколько минут меньше затратил на путь из A в B велосипедист, чем пешеход?
16. За 40 минут пешеход прошел 3 километра. Сколько километров он пройдет за 1 час, если будет идти с той же скоростью?
17. На карте показан путь Лены от дома до школы. Лена измерила длину каждого участка и подписала его. Используя рисунок, определите длину пути (в м), если масштаб 1 см : 10 000 см.
18. Какая из следующих круговых диаграмм показывает распределение площадей океанов в Мировом Океане, если Тихий Океан занимает около 48% всего Мирового Океана, Атлантический — 26%, Индийский — 21% и Северный Ледовитый — 5%?
19. В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.
20. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле C = 150 + 11 · (t − 5), где t — длительность поездки, выраженная в минутах (t 5). Пользуясь этой формулой, рассчитайте стоимость 14-минутной поездки.
21. Решите уравнение
22. Из пяти следующих утверждений о результатах матча хоккейных команд "Транспортир" и "Линейка" четыре истинны, а одно — ложно. Определите, с каким счетом закончился матч, и укажите победителя (если матч завершился победой одной из команд). Ответ обоснуйте.
1) Выиграл "Транспортир".
2) Всего в матче было заброшено менее 10 шайб.
3) Матч закончился вничью.
4) Всего в матче было заброшено более 8 шайб.
5) "Линейка" забросила более 3 шайб.
23. Постройте график функции и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
24. Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK = 20.
25. Середины сторон параллелограмма является вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
26. В прямоугольном треугольнике  катет
катет  равен 8, катет
равен 8, катет  равен 15. Найдите радиус окружности, которая проходит через концы гипотенузы треугольника и касается прямой
равен 15. Найдите радиус окружности, которая проходит через концы гипотенузы треугольника и касается прямой  .
.







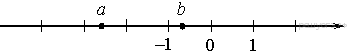

 В треугольнике
В треугольнике  В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.









