Министерство общего и профессионального образования
Свердловской области
Управление образования Администрации города Нижний Тагил
Муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа № 30
Направление: научно-техническое
Секция: «Математика и информационные технологии»
Вероятность получения положительной отметки при написании тестовой работы путём угадывания правильного ответа
Научный руководитель:
Глазер Анна Геннадьевна,
учитель математики
Нижний Тагил
2020 год
Оглавление
| ВВЕДЕНИЕ…………………………………………………………………….. | 3 |
| ГЛАВА 1. Теория вероятностей………………………………………………. | 5 |
| 1.1. | История становления теории вероятностей………………………… | 5 |
| 1.2. | Определение и основные формулы теории вероятностей…………. | 8 |
| 1.3. | История применения методов теории вероятностей……………….. | 13 |
| ГЛАВА 2. Расчёт вероятности получения положительной отметки………... | 16 |
| 2.1. | Анализ выполнения тестовых работ………………………………… | 16 |
| 2.2. | Применение формул Бернулли и классической вероятности для вычисления искомой вероятности………………………………….. |
24 |
| ЗАКЛЮЧЕНИЕ……………………………………………………………….. | 29 |
| СПИСОК ЛИТЕРАТУРЫ……………………………………………………… | 31 |
| ПРИЛОЖЕНИЕ 1. ……………………………………………………………... | 32 |
| ПРИЛОЖЕНИЕ 2. ……………………………………………………………... | 33 |
| ПРИЛОЖЕНИЕ 3. …………………………………………………………….. | 34 |
| ПРИЛОЖЕНИЕ 4. …………………………………………………………….. | 35 |
| ПРИЛОЖЕНИЕ 5. …………………………………………………………….. | 37 |
Введение
Случай, случайность — с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная находка, случайная ошибка. Этот ряд можно продолжать бесконечно. Казалось бы, тут нет места для математики, но и здесь наука обнаружила интересные закономерности - они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
Одной из современных технологий контроля и диагностики учебных достижений учащихся является - тестовая технология. Что же такое тест? В наши дни существует много видов тестов, поэтому дать универсальное определение для всех видов тестов вряд ли можно.
Если мы говорим о педагогическом тестировании, то на наш взгляд, больше подойдет следующее определение: тест является объективным методом контроля знаний учащегося, инструментом, позволяющим выявить факт усвоения. Так почему же ученик, который готовился к тесту, может написать его хуже, чем другой ученик, выполнивший тест путём угадывания ответа?
Случай или случайность? С подобными вопросами мы сталкиваемся ежедневно. Кажется, как можно «предвидеть» наступление случайного события? Ведь оно может произойти, а может и нет. Но математика нашла способы оценивать вероятность наступления случайных событий. Этим и определяется актуальность нашей работы.
Из всего вышеизложенного, мы определили цель нашей работы: определить вероятность получения положительной оценки при написании тестовой работы путём угадывания ответа.
Для достижения этой цели мы поставили перед собой следующие задачи:
Изучить теоретический материал по данной теме, используя справочную литературу и ресурсы интернета.
Обобщить полученные результаты.
Провести статистический эксперимент с помощью тестовых работ по алгебре, ОБЖ и истории в 9А классе.
Проанализировать данные, полученные путем статистического эксперимента.
Объект исследования: результаты написания тестовых работ.
Предмет исследования: вероятность получения положительной отметки.
Гипотеза: получение положительной оценки при написании тестовой контрольной работы путём угадывания ответа возможно, но вероятность такого исхода будет мала.
ГЛАВА 1. Теория вероятностей
История становления теории вероятностей
Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год).
Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
Следующий (второй) период истории теории вероятностей ( XVIII в. и начало ХIХ в.) связан с именами А. Муавра (Англия), П. Лапласа (Франция), К. Гаусса (Германия) и С. Пуассона (Франция). Они доказали первые предельные теоремы. Карл Гаусс детально исследовал нормальное распределение случайной величины, также называемое «распределением Гаусса».
Это - период, когда теория вероятностей уже находит ряд весьма актуальных применений в естествознании и технике (главным образом в теории ошибок наблюдений, развившейся в связи с потребностями геодезии и астрономии, и в теории стрельбы).
Третий период истории теории вероятностей, (вторая половина XIX в.) связан в основном с именами русских математиков П. Л. Чебышева, А. М. Ляпунова и А. А. Маркова (старшего). Теория вероятностей развивалась в России и раньше (в XVIII в. ряд трудов по теории вероятности был написан работавшими в России Л. Эйлером, Н. Бернулли и Д. Бернулли; во второй период развития теории вероятностей следует отметить работы М. В. Остроградского по вопросам теории вероятностей,связанным с математической статистикой, и В. Я. Буняковского по применениям теории вероятностей к страховому делу, статистике и демографии).
Теория вероятностей - математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом с первыми. Утверждение о том, что какое-либо событие наступает с вероятностью, равной, например, ½, ещё не представляет само по себе окончательной ценности, так как мы стремимся к достоверному знанию. Окончательную познавательную ценность имеют те результаты теории вероятностей, которые позволяют утверждать, что вероятность наступления какого-либо события А весьма близка к единице или (что то же самое) вероятность не наступления события А весьма мала.
Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики. Он дал наиболее совершенное аксиоматическое построение теории вероятностей, связав ее с одним из важнейших разделов современной математики метрической теорией функций. Особое значение работы А. Н. Колмогорова имеют в области теории случайных функций (стохастических процессов), которые в настоящее время являются основой всех исследований в данной области. Работы А. Н. Колмогорова, относящиеся к оценке эффективности легли в основу целого нового научного направления в теории стрельбы, переросшего затем в более широкую науку об эффективности боевых действий. [4,6]
Развитие зарубежной теории вероятностей в настоящее время также идет усиленными темпами в связи с настоятельными требованиями практики. Преимущественным вниманием пользуются, как и у нас, вопросы, относящиеся к случайным процессам. Значительные работы в этой области принадлежат Н. Винеру, В. Феллеру, Д. Дубу. Важные работы по теории вероятностей и математической статистике принадлежат Р. Фишеру, Д. Нейману и Г. Крамеру. [10]
На основании вышесказанного мы можем констатировать, теория вероятностей, подобно другим разделам математики, развилась из потребностей практики, и абстрактно она отражает закономерности в массовых случайных событиях. Эти закономерности играют очень важную роль в различных областях естествознания, медицине, технике, экономике, военном деле. Многие разделы теории вероятностей были развиты благодаря запросам практики.
1.2. Определение и основные формулы теории вероятностей
Классическое определение теории вероятности - раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
Следуя классическому определению, вероятность события определяется как отношение благоприятных событий к общему количеству событий.
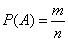 , где n - общее число равновероятных исходов; m - число исходов, благоприятных событию А. [1, стр. 31]
, где n - общее число равновероятных исходов; m - число исходов, благоприятных событию А. [1, стр. 31]
Теория вероятности - раздел математики, изучающий закономерности возникновения случайных явлений. [5]
Педагогические явления относятся к числу массовых: они охватывают большие совокупности людей, повторяются из года в год, совершаются непрерывно. Показатели (параметры, результаты) педагогического процесса имеют вероятностный характер: одно и то же педагогическое воздействие может приводить к различным следствиям (случайные события, случайным величинам). Тем не менее, при многократном воспроизведении условий определенные следствия появляются чаще других, - это и есть проявление так называемых статистических закономерностей (изучением которых занимаются теория вероятностей и математическая статистика).
Случайная величина (СВ) – это численная характеристика, измеряемая по ходу опыта и зависящая от случайного исхода. СВ реализуемая по ходу опыта и сама является случайной. Каждая СВ задает распределение вероятностей.
Основным свойством педагогических процессов, явлений служит их вероятностный характер (при данных условиях они могут произойти, реализоваться, но могут и не произойти). Для таких явлений существенную роль играет понятие вероятности.
Вероятность (Р) показывает степень возможности осуществления данного события, явления, результата. Вероятность невозможного события равна нулю p = 0, достоверного - единице p = 1 (100%). Вероятность любого события лежит в пределах от 0 до 1, в зависимости от того, насколько это событие случайно.
Если мы интересуемся событием A, то, скорее всего, можем наблюдать, фиксировать факты его появления. Потребность в понятии вероятности и ее вычисления возникнет, очевидно, только тогда, когда мы наблюдаем это событие не каждый раз, либо осознаем, что оно может произойти, а может не произойти. И в том и другом случае полезно использовать понятие частоты появления события f(A) - как отношения числа случаев его появления (благоприятных исходов) к общему числу наблюдений. Частота наступления случайного события зависит не только от степени случайности самого события, но и от числа (количества) наблюдений за этой СВ.
Существует два вида выборок СВ: зависимые и независимые. Если результаты измерения некоторого свойства у объектов первой выборки не оказывают влияния на результаты измерения этого свойства у объектов второй выборки, то такие выборки считаются независимыми. В тех случаях, когда результаты одной выборки влияют на результаты другой выборки, выборки считают зависимыми. Классический способ получения зависимых измерений – это двукратное измерение одного и того же свойства (или разных свойств) у членов одной и той же группы.
Событие А не зависит от события В, если вероятность события А не зависит от того произошло или нет событие В. События А и В независимы, если Р(АВ)=Р(А)Р(В). На практике независимость события устанавливается из условий опыта, интуиции исследователя и практики.
Закон распределения СВ
Подчиняются ли каким-либо законам явления, носящие случайный характер? Да, но эти законы отличаются от привычных нам физических законов. Значения СВ невозможно предугадать даже при известных условиях эксперимента, мы можем лишь указать вероятности того, что СВ примет то или иное значение. Зато зная распределение вероятностей СВ, мы можем делать выводы о событиях, в которых участвуют эти случайные величины. Правда, эти выводы будут также носить вероятностный характер.
Пусть некоторая СВ является дискретной, т.е. может принимать лишь фиксированные значения Xi. В этом случае ряд значений вероятностей P(Xi) для всех (i=1…n) допустимых значений этой величины называют её законом распределения.
Закон распределения СВ - это отношение, устанавливающее связь между возможными значениями СВ и вероятностями, с которыми принимаются эти значения. Закон распределения полностью характеризует СВ.
При построении математической модели для проверки статистической гипотезы необходимо ввести математическое предположение о законе распределения СВ (параметрический путь построения модели).
Непараметрический подход к описанию математической модели (СВ не имеет параметрического закона распределения) менее точен, но имеет более широкую область применения.
Точно также, как и для вероятности случайного события, для закона распределения СВ есть только два пути его отыскания. Либо мы строим схему случайного события и находим аналитическое выражение (формулу) вычисления вероятности, либо придется использовать эксперимент и по частотам наблюдений делать какие–то предположения (выдвигать гипотезы) о законе распределения.
Конечно же, для каждого из "классических" распределений уже давно эта работа проделана – широко известными и очень часто используемыми в прикладной статистике являются биномиальное и полиномиальное распределения, геометрическое и гипергеометрическое, распределение Паскаля и Пуассона и многие другие.
Для почти всех классических распределений немедленно строились и публиковались специальные статистические таблицы, уточняемые по мере увеличения точности расчетов.
Сегодня положение изменилось – нет нужды хранить данные расчетов по формулам, время на использование закона распределения для практики сведено к минутам, а то и секундам. Уже сейчас существует достаточное количество разнообразных пакетов прикладных компьютерных программ для этих целей.
Среди всех вероятностных распределений есть такие, которые используются на практике особенно часто. Эти распределения детально изучены и свойства их хорошо известны. Многие из этих распределений лежат в основе целых областей знаний – таких, как теория массового обслуживания, теория надежности, контроль качества, теория игр и т.п. [9]
Биномиальное распределение (распределение Бернулли)
Возникает в тех случаях, когда ставится вопрос: сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях.
Для удобства и наглядности будем полагать, что нам известна величина p – вероятность того, что учащийся, написавший тест, получит положительную оценку и (1– p) = q – вероятность того, что учащийся, написавший тест, не получит положительную оценку.
Если X – число учащихся с положительной оценкой из общего числа n учащихся, то вероятность того, что среди n учащихся оказалось k учащихся с положительной оценкой равна.
P(X= k) = 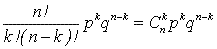 , где k=0,1,…n
, где k=0,1,…n
Данную формулу называют формулой Бернулли. При большом числе испытаний биномиальное распределение стремиться к нормальному. [1, стр.39]
Распределение Пуассона
Играет важную роль в ряде вопросов физики, теории связи, теории надежности, теории массового обслуживания и т.д. Всюду, где в течение определенного времени может происходить случайное число каких-то событий (радиоактивных распадов, телефонных вызовов, отказов оборудования, несчастный случаях и т.п.).
Рассмотрим наиболее типичную ситуацию, в которой возникает распределение Пуассона. Пусть некоторые события (покупки в магазине) могут происходить в случайные моменты времени. Определим число появлений таких событий в промежутке времени от 0 до Т.
Случайное число событий, происшедших за время от 0 до Т, распределено по закону Пуассона с параметром l = аТ, где а 0 - параметр задачи, отражающий среднюю частоту событий. Вероятность k покупок в течение большого интервала времени, (например, – дня) составит
P(Z=k) = 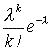 [3, стр. 78]
[3, стр. 78]
Равномерное распределение
Равномерное распределение вероятностей является простейшим и может быть как дискретным, так и непрерывным. Дискретное равномерное распределение – это такое распределение, для которого вероятность каждого из значений СВ одна и та же, то есть:
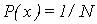
где N – количество возможных значений СВ.
Распределение вероятностей непрерывной CВ Х, принимающие все свои значения из отрезка [а;b] называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю:
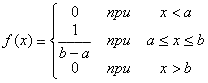 [11]
[11]
Подводя итоги вышесказанному необходимо отметить, что данный раздел математики изучает закономерности, присущие массовым случайным явлениям. При этом изучаемые явления рассматриваются в абстрактной форме, независимо от их конкретной природы.
1.3. История применения методов теории вероятностей
Начать по праву следует со статистической физики. Современное естествознание исходит из представления, согласно которому все явления природы носят статистический характер и законы могут получить точную формулировку только в терминах теории вероятностей. Статистическая физика стала основой всей современной физики, а теория вероятностей – ее математическим аппаратом. В статистической физике рассматриваются задачи, которые описывают явления, определяющиеся поведение большого числа частиц. Статистическая физика весьма успешно применяется в самых разных разделах физики. В молекулярной физике с ее помощью объясняют тепловые явления, в электромагнетизме – диэлектрические, проводящие и магнитные свойства тел, в оптике она позволила создать теорию теплового излучения, молекулярного рассеивания света. В последние годы круг приложений статистической физики продолжает расширяться.
Статистические представления позволили быстро оформить математическое изучение явлений ядерной физики. Появление радиофизики и изучение вопросов передачи радио сигналов не только усилили значение статистических концепций, но и привели к прогрессу самой математической науки – появлению теории информации.
Понимание природы химических реакций, динамического равновесия также невозможно без статистических представлений. Вся физическая химия, ее математический аппарат и предлагаемые ею модели являются статистическими.
Астрономия в ряде своих разделов использует статистический аппарат. Именно для использования в астрономии был разработан знаменитый “метод наименьших квадратов” (Лежандр 1805, Гаусс 1815). Главной задачей, для решения которой он был первоначально использован, стал расчет орбит комет, который приходилось производить по малому числу наблюдений. Ясно, что надежное определение типа орбиты (эллипс или гипербола) и точный расчет ее параметров оказывается трудным, так как орбита наблюдается лишь на небольшом участке. Метод оказался эффективным, универсальным, и вызвал бурные споры о приоритете. Его стали использовать в геодезии и картографии.
Биологи заметили, что разброс размеров органов живых существ одного и того же вида прекрасно укладывается в общие теоретико-вероятностные законы. В 1870-1900 годах бельгиец Кетле и англичане Френсис Гальтон и Карл Пирсон основали новое научное направление – биометрию, в которой впервые стала систематически и количественно изучаться неопределенная изменчивость живых организмов и наследование количественных признаков. В научный оборот были введены новые понятия – регрессии и корреляции.
Итак, вплоть до начала 20 века основные приложения теории вероятности были связаны с научными исследованиями. Внедрение в практику – сельское хозяйство, промышленность, медицину произошло в 20 веке.
Гуманитарные науки объединяют очень разнообразные по характеру дисциплины – от языкознания и литературы до психологии и экономики. Статистические методы все в более значительной мере начинают привлекаться к историческим исследованиям, особенно в археологии. Статистический подход используется для расшифровки надписей на языке древних народов. Искусство шифрования и дешифровки основано на использовании статистических закономерностей языка. Другие направления связаны с изучением повторяемости слов и букв, распределения ударений в словах, вычислением информативности языка конкретных писателей и поэтом. Статистические методы используются для установления авторства и изобличения литературных подделок. Например, авторство М.А. Шолохова по роману «Тихий Дон» было установлено с привлечением вероятностно-статистических методов.
Широкое применение статистических методов в медицине началось сравнительно недавно (вторая половина 20 века). Развитие эффективных методов лечения (антибиотики, инсулин, эффективная анестезия, искусственное кровообращение) потребовало достоверных методов оценки их эффективности. Возникло новое понятие “Доказательная медицина”. Начал развиваться более формальный, количественный подход к терапии многих заболевании – введение протоколов.
Таким образом, статистические методы сегодня стали неотъемлемой частью педагогических измерений, поскольку без них при решении целого ряда исследовательских задач невозможно дать объективную интерпретацию результатов измерений. Дело в том, что психолого-педагогические измерения, выполненные с помощью различных тестов, опросников, всегда сопровождаются некоторой ошибкой, которую вызывают несовершенство диагностического инструментария (чаще всего он отражает некоторую модель изучаемого объекта, которая никогда не бывает абсолютно тождественной его сущности), различные обстоятельства, связанные с условиями проведения измерений. Поэтому результат психолого-педагогического исследования имеет вероятностный характер, следовательно, необходимо доказывать статистическую достоверность (значимость) полученных результатов. Это и обусловило применение в педагогике статистических методик сравнения уровней исследуемых параметров. Мы рассматриваем лишь некоторые примеры использования статистических методов и процедур обработки результатов измерений.
ГЛАВА 2. Расчет вероятности получения положительной отметки
2.1. Анализ выполнения тестовых работ
Для нашего исследования, мы решили установить процент успешности выполнения тестовых контрольных работ. Для этого мы провели несколько тестовых работ среди учащихся 9А класса. Данное исследование проводилось посредством выполнения учащимися тестовых контрольных работ по математике, ОБЖ и истории. В выполнении работ по математике и истории приняли участие 20 учащихся, при выполнении работы по ОБЖ приняли участие 15 учащихся.
В качестве материала для исследования мы взяли задания с выбором одного правильного варианта ответа из открытого банка заданий ОГЭ по математике и истории, а так же контрольную работу с выбором правильного варианта ответа по ОБЖ.
Тестовая работа по математике и ОБЖ состояла из 10 заданий к каждому из которых предлагалось четыре варианта ответа, один из которых правильный. (см. Приложение 1,3)Тестовая работа по истории состояла из 12 заданий к каждому из которых предлагалось четыре варианта ответа, один из которых правильный. (см. Приложение 2)
Для того чтобы получить положительную отметку достаточно было ответить на 5 вопросов.
При выполнении данных работ в одинаковых условиях мы получили различные результаты.
После проверки всех тестовых работ данные распределились таким образом:
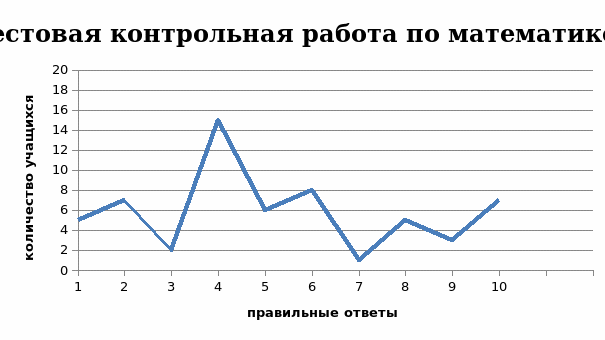
Рис.1. Количество правильных ответов полученных при выполнении тестовой работы в разрезе каждого ученика.
Анализ работ показал, что максимальное количество правильно угаданных ответов в тестовой контрольной работе в разрезе каждого ученика равно 3, что не позволяет ученику получить положительной отметки.
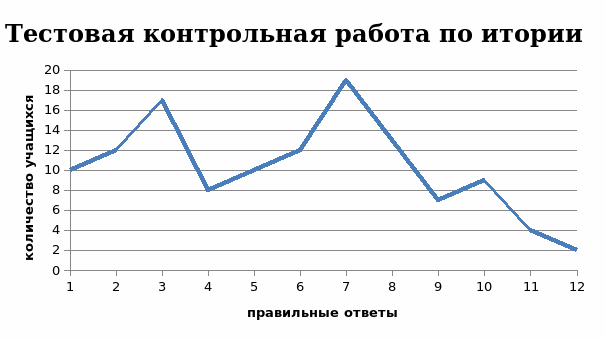
Рис.2. Количество правильных ответов полученных при выполнении тестовой работы в разрезе каждого ученика.
Анализ работ показал, что максимальное количество правильно угаданных ответов в тестовой контрольной работе в разрезе каждого ученика равно 4, что не позволяет ученику получить положительной отметки. Так же встречаются работы с 5 и 8 правильными ответами.
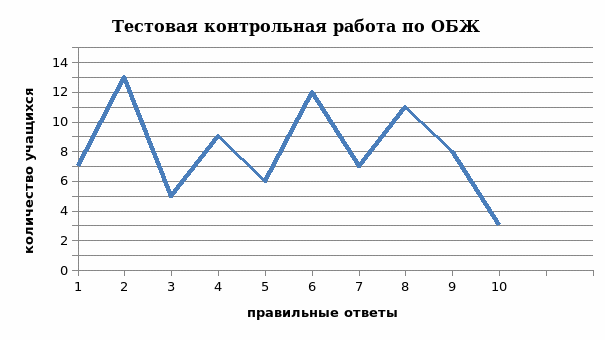
Рис.3. Количество правильных ответов полученных при выполнении тестовой работы в разрезе каждого ученика.
Анализ работ показал, что максимальное количество правильно угаданных ответов в тестовой контрольной работе в разрезе каждого ученика равно 3, что не позволяет ученику получить положительной отметки. Но при этом стоит отметить, что увеличивается количество работ в которых встречаются 5 и более правильных ответов.
Для более наглядного изображения, мы представили полученные данные в виде диаграмм.
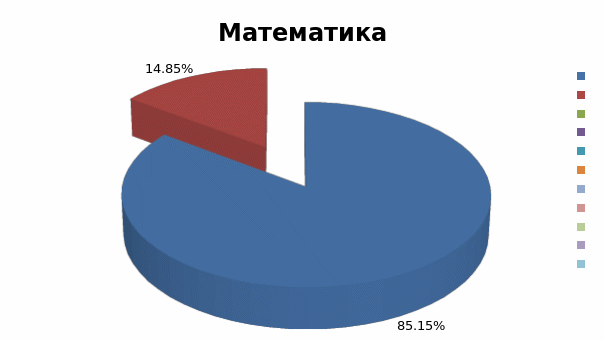
Рис.4. Распределение полученных оценок, в процентном отношении, при выполнении тестовой работы.
Таким образом, при выполнении данной работы ни один ученик не смог выполнить данную работу на повышенном уровне, три учащихся ответили на пять вопросов правильно, т.е. получили отметку три и семнадцать учащихся не смогли преодолеть минимальный барьер.
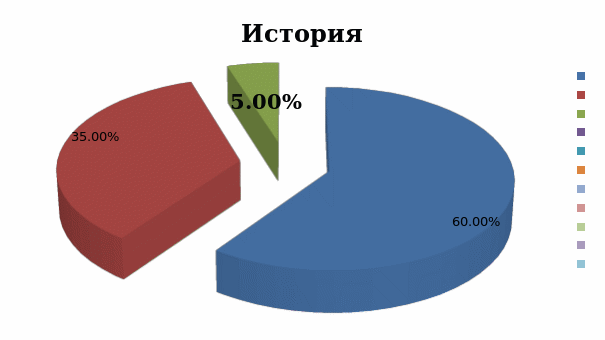
Рис.5. Распределение полученных оценок, в процентном отношении, при выполнении тестовой работы.
При выполнении тестовой контрольной работы по истории всего один ученик выполнил работу на повышенном уровне, семь учащихся ответили на пять вопросов правильно, остальные не справились с заданиями.
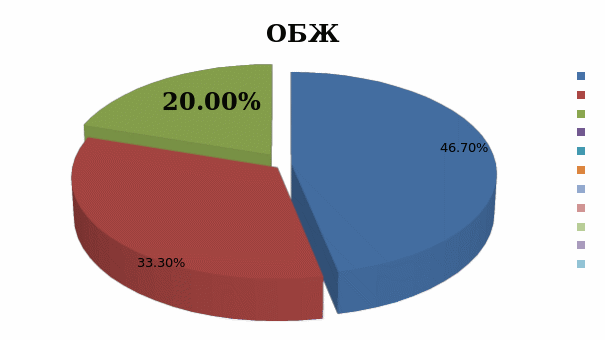
Рис.6. Распределение полученных оценок, в процентном отношении, при выполнении тестовой работы.
При выполнении тестовой контрольной работы по ОБЖ три ученика выполнили работу на повышенном уровне, пять учащихся ответили на пять вопросов правильно, остальные не справились с заданиями.
Подводя промежуточные итоги, мы можем сказать, что с работами гуманитарной направленности учащиеся 9А класса справились лучше, чем с работой по математике.
Для того, чтобы наше исследование было более полным, мы решили установить процент успешности выполнения тестовых контрольных работ в которых из предложенных вариантов ответов необходимо было выбрать несколько вариантов ответов.
Для этого мы провели несколько тестовых работ среди учащихся того же класса. Данное исследование проводилось посредством выполнения учащимися тестовых контрольных работ по математике и биологии. В выполнении работ по математике приняли участие 20 учащихся, при выполнении работы по биологии приняли участие 16 учащихся.
В качестве материала для исследования мы взяли задания с выбором одного правильного варианта ответа из открытого банка заданий ОГЭ по математике и биологии.
Тестовая работа по математике состояла из 10 заданий, к каждому из которых предлагалось четыре варианта ответа, два из которых правильные. (см. Приложение 4) Тестовая работа по биологии состояла из 10 заданий, к каждому из которых предлагалось шесть вариантов ответов, три из которых правильные. (см. Приложение 5)
Для того чтобы получить положительную отметку достаточно было ответить на 5 вопросов. При выполнении данных работ в одинаковых условиях мы получили различные результаты.
После проверки всех тестовых работ данные распределились таким образом:
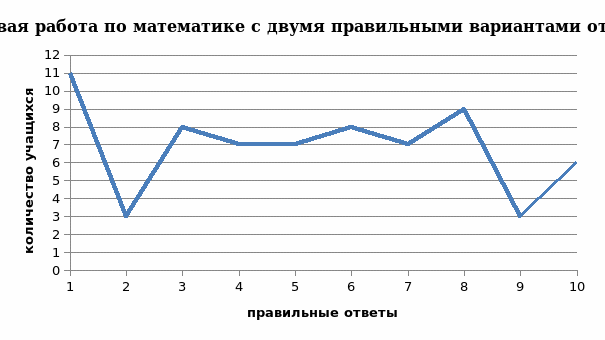
Рис.7. Количество правильных ответов полученных при выполнении тестовой работы в разрезе каждого ученика.
Анализ работ показал, что чаще встречающееся максимальное количество правильно угаданных ответов в тестовой контрольной работе в разрезе каждого ученика равно 3, что не позволяет ученику получить положительной отметки. Так же встречаются работы с 4 и 5 правильными ответами.
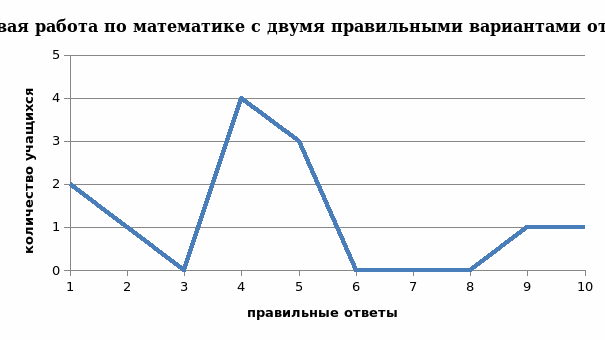
Рис.8. Количество правильных ответов полученных при выполнении тестовой работы в разрезе каждого ученика.
Анализ работ показал, что чаще встречающееся максимальное количество правильно угаданных ответов в тестовой контрольной работе в разрезе каждого ученика равно 1, что не позволяет ученику получить положительной отметки. Так же встретилась одна работа с 4 правильными ответами.
Для более наглядного изображения, мы представили полученные данные в виде диаграмм.
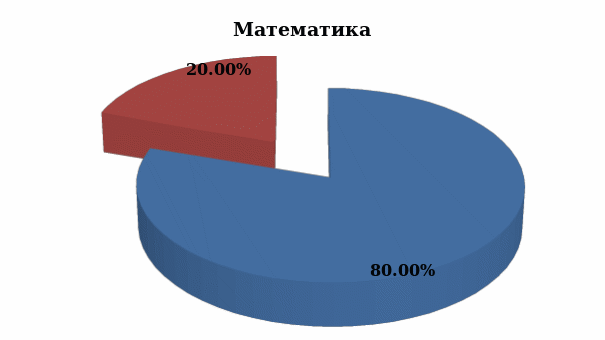
Рис.9. Распределение полученных оценок, в процентном отношении, при выполнении тестовой работы.
При выполнении тестовой работы по математике четыре ученика выполнили работу на повышенном уровне, остальные не справились с заданиями.
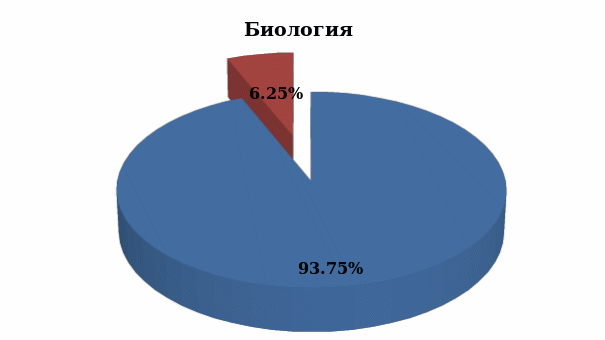
Рис.10. Распределение полученных оценок, в процентном отношении, при выполнении тестовой работы.
При выполнении тестовой работы по биологии только один ученик набрал достаточное количество баллов, достаточных для получения отметки три, остальные не справились с заданиями.
Таким образом, проанализировав все работы, выполненные учащимися 9А класса, можно сделать вывод о том, что с увеличением вариантов ответов уменьшается количество работ, выполненных на оценку выше двойки.
2.2. Применение формул Бернулли и классической вероятности для вычисления искомой вероятности
Применяя же полученные ранее данные к теме нашего исследования, мы получаем:
Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании тестовой работы по математике. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т. е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда по классическому определению вероятности наступления события p = P(A)=1/4. Вероятность противоположного события q = P(А)=1-p = 3/4.
Таким образом, вероятность получения положительной оценки составляет 0,25, применяя для вычисления формулу классической вероятности.
Так же применив формулу Бернулли к вычислению вероятности положительной отметки мы получили следующие результаты:
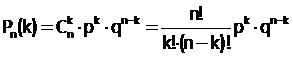
р = 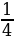 ( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
q = 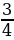 (q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
(q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
k=20 (к – количество участников тестирования);
n=40 (n – количество вариантов ответов).
Pn(k) = 137846528820,00
137846528820,00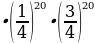 0,000397577
0,000397577
Точно такие же вычисления мы применили для тестовой работы по ОБЖ.
Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании тестовой работы по математике. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т. е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда по классическому определению вероятности наступления события p = P(A)=1/4. Вероятность противоположного события q = P(А)=1-p = 3/4.
Таким образом вероятность получения положительной оценки составляет 0,25, применяя для вычисления формулу классической вероятности.
Так же применив формулу Бернулли к вычислению вероятности положительной отметки мы получили следующие результаты:
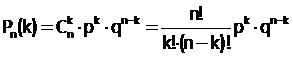
р = 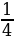 ( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
q = 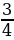 (q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
(q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
k= 15(к – количество участников тестирования);
n= 40 (n – количество вариантов ответов).
Pn(k) =  40225345056
40225345056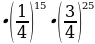 0,028192363934
0,028192363934
Так же мы вычислили вероятность получения положительной оценки при выполнении тестовой работы по истории:
Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании тестовой работы по математике. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т. е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда по классическому определению вероятности наступления события p = P(A)=1/4. Вероятность противоположного события q = P(А)=1-p = 3/4.
Таким образом вероятность получения положительной оценки составляет 0,25, применяя для вычисления формулу классической вероятности.
Так же применив формулу Бернулли к вычислению вероятности положительной отметки мы получили следующие результаты:
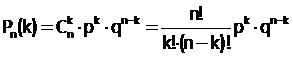
р = 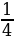 ( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
q = 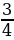 (q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
(q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
k= 20(к – количество участников тестирования);
n= 48 (n – количество вариантов ответов).
Pn(k) =  16735679449896
16735679449896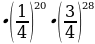 0,0048323557333
0,0048323557333
Сравнивая результаты расчетов применения формулы классической вероятности и формулы Бернулли, можно сделать следующие выводы:
анализируя полученные результаты, наибольший процент правильно угаданных ответов был получен при написании теста по ОБЖ. Возможно, это связано с тем, что учащиеся опирались на те знания, которые они получают в повседневной жизни и им было легче выбирать ответ, опираясь на свой жизненный опыт. Наименьший же процент пришелся на алгебру, что, скорее всего, связано с неумелым применением математических знаний в повседневной жизни;
при использовании формулы классической вероятности результат получается один и тот же, т.к. в данных расчетах не учитывается количество заданий и количество участников тестирования. Таким образом, результат получается менее точным.
Так же мы решили посмотреть, как же будет себя вести вероятность получения положительной оценки путем угадывания правильного ответа, если увеличить количество правильных ответов из большего количества вариантов ответов.
Применяя полученные ранее данные к теме нашего исследования, мы получаем:
Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании тестовой работы по математике. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т. е. правильно угаданный ответ, а таких случаев 2), к числу всех случаев (таких случаев 4).
Применив формулу Бернулли к вычислению вероятности получения положительной отметки, выполняя тестовую работу по математике, мы получили следующие результаты:
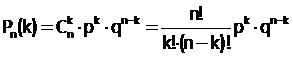
р = 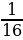 ( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
q = 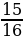 (q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
(q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
k= 20(к – количество участников тестирования);
n= 40 (n – количество вариантов ответов).
Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании тестовой работы по математике. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т. е. правильно угаданный ответ, а таких случаев 2), к числу всех случаев (таких случаев 4).
Pn(k) = 137846528820,00 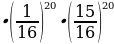 0,00000000000003136329
0,00000000000003136329
Применив формулу Бернулли к вычислению вероятности получения положительной отметки выполняя тестовую работу по биологии мы получили следующие результаты:
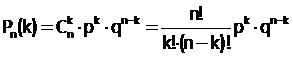
р = 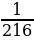 ( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
q = 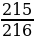 (q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
(q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
k= 16(к – количество участников тестирования);
n= 60 (n – количество вариантов ответов).
Pn(k) = 49869458618175,00 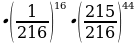 0,000000000000000000000001810931
0,000000000000000000000001810931
Сравнивая полученные расчеты можно сделать следующий вывод, вероятность получения положительной отметки путем угадывания правильного варианта ответа хоть и мала, но заметно уменьшается пропорционально количеству правильных вариантов ответов из предложенного количества. Т.е. чем больше вариантов, тем меньше вероятность угадывания правильного ответа.
Заключение
Событие называется случайным, если в результате испытания (опыта) оно может произойти, а может и нет. Строго говоря, случайное событие нельзя предугадать заранее в принципе. Непредсказуемость наступления того или иного события и есть отличительная черта случайного события. Тем не менее, с помощью математических методов есть возможность проанализировать некоторые случайные события.
Наша исследовательская работа позволяет сделать вывод о том, что изучив теоретический материал по теме можно подвергнуть анализу вероятность получения положительной оценки при написании тестовой работы путем угадывания правильного ответа. Для этого мы не только изучили учебную литературу, а так же провели и проанализировали статистический эксперимент.
На основании проведенного нами исследования, можно сделать следующие выводы:
измерения, выполненные с помощью различных тестов, опросников, всегда сопровождаются некоторой ошибкой, которую вызывают несовершенство диагностического инструментария, именно поэтому результат психолого-педагогического исследования имеет вероятностный характер;
вероятность получения положительной оценки при написании тестовой работы в различных областях науки будут отличаться;
вероятность получения положительной оценки при написании тестовой работы зависит от личного опыта испытуемого, его личных качеств и общей эрудированности;
вероятность получения положительной отметки на прямую зависит от количества правильных вариантов ответов из общего количества предложенных вариантов для выбора.
Таким образом, гипотеза, которую мы выдвинули ранее, подтвердилась. Полученные данные позволяют сделать вывод о том, что получение положительной оценки при написании тестовой контрольной работы путём угадывания правильного ответа, возможно. Но вероятность такого исхода будет мала.
Исследования в этом направлении могут быть продолжены. Это могло бы быть изучение не только тестовых контрольных работ с выбором правильного варианта ответа из предложенных, но и работ, в которых есть «открытые» вопросы, т.е. требующие непосредственного ответа на поставленный вопрос.
Список литературы
Балдин, К.В. Теория вероятностей и математическая статистика: Учебник / К.В. Балдин, В.Н. Башлыков, А.В Рукосуев. - М.: Дашков и К, 2016. – 472 c.
Бродский Я.С. «Статистика. Вероятность. Комбинаторика»-М.: Оникс; Мир и Образование, 2008. – 296 с. Лютикас В.С. Факультативный курс по математике: Теория вероятностей.-М.:Просвещение 1990. – 161 с.
Майстров Л.Е. Развитие теории вероятностей. М.:Наука, 1980 г. – 270 с.
Ожегов, С.И. Толковый словарь русского языка / С.И. Ожегов, Н.Ю. Шведова. - М.: ИТИ Технологии; Издание 4-е, доп., 2015. - 944 c.
Тарасов Л.В. Мир, построенный на вероятности. М., Пр., 1984. – 162 с.
Федосеев В.Н .Элементы теории вероятностей для VII-IX классов средней школы.//Математика в школе.-2002.-№4,5.
Яковлев, В.П. Теория вероятностей и математическая статистика: Учебное пособие / В.П. Яковлев. - М.: Дашков и К, 2012. - 184 c
Студопедия.нет Информационный студенческий ресурс. [Электронный ресурс] – Режим доступа: https://studopedia.ru
МегаОбучалка [Электронный ресурс] – Режим доступа: https://megaobuchalka.ru
Википедия. Свободная энциклопедия. [Электронный ресурс] – Режим доступа: https://ru.wikipedia.org
Решу ОГЭ. Образовательный портал. [Электронный ресурс] – Режим доступа: https://sdamgia.ru
Приложение 1. Тестовая работа по математике

Приложение 2. Тестовая работа по истории

Приложение 3. Тестовая контрольная работа по ОБЖ

Приложение 4. Тестовая работа по математике 2 варианта ответа


Приложение 5. Тестовая работа по биологии 3 варианта ответа


19







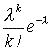 [3, стр. 78]
[3, стр. 78]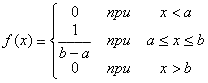 [11]
[11]









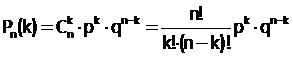
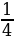 ( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);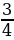 (q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
(q - вероятность того, что учащийся, написавший тест, не получит положительную оценку); 137846528820,00
137846528820,00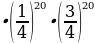 0,000397577
0,000397577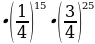 0,028192363934
0,028192363934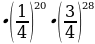 0,0048323557333
0,0048323557333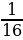 ( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);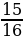 (q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
(q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);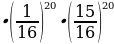 0,00000000000003136329
0,00000000000003136329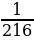 ( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);
( р - вероятность того, что учащийся, написавший тест, получит положительную оценку);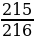 (q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);
(q - вероятность того, что учащийся, написавший тест, не получит положительную оценку);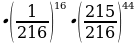 0,000000000000000000000001810931
0,000000000000000000000001810931
















