Координатно – векторный способ решения стереометрических задач.
Работу выполнила
учитель математики ГБОУ СОШ № 47
Тадтаева Залина Зауровна.
г.Владикавказ
ноябрь 2016 г.
Введение.
Со второй половины двадцатого века в программах и учебниках школьной геометрии определенной место стало уделятся изучению элементов векторной алгебры. И это вполне закономерно, так как аппарат векторной алебры находит свое широкое применение в геометрии линейных векторных пространств ( аналитической геометрии), теории линейного программирования.Кроме того, аппарат и методы векторной алгебры лежат в основе векторного анализа, они широко используются в курсах физики, теоретической механики и математической физики, дифференциальной геометрии и многих других естественнонаучных теориях. Более того, векторный метод лежит в основе аксиоматического построения геометрии (аксиоматика Г.Вейля)1.
Многообразие возможностей применения векторного аппарата и его роль в повышении и развитии математической культуры учащихся трудно переоценить. Изучение этого материала становится особенно актуальным,когда речь идет о подготовке учащихся к сдаче ЕГЭ по математике и особенно при решении задач части С (задачи № 14, стереометрические задачи).Заметим, что векторное решение многих стереометрических задач значительно проще их решения средствами элементарной геометрии и при этом обойтись без тех дополнительных построений, которые затрудняют поиск решения задачи.Более того, применение векторов при решении геометрических задач способствует поиску итересных обобщений, которые могут возникнуть при анализе полученных решений.Чтобы векторы стали аппаратом решения геометрических задач, необходимо научиться:
1)переводить условие геометрической задачи в векторную теримнологию и символику, т.е. на « векторный язык»;
2)грамотно выполнять необходимые алгебраические операции над векторами;
3)результат, полученный в векторной форме, переводить на язык геометрии.
Предложенный материал , на мой взгляд, покажет вам преимущества применения векторного метода при решении стереометрических задач на взаимное расположение прямых и плоскостей ( аффинные задачи) и нахождение расстояния, углов( метрические задачи).
Напомню основные понятия и знания, которые необходимо актуализировать:
Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
Расстояние между двумя параллельными прямыми равно длине отрезка их общего перепндикуляра;
Расстояние между параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой;
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра , опущеного из этой точки на плоскость;
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра( растояние от любой точки прямой до указанной плоскости);
Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра( расстояние между точкой одной из этих плоскостей и другой плоскостью);
Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых, образованных при пересечении прямых ( 0º );
);
Углом между двумя скрещивающимися прямыми , называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся;
Две прямые называются перпендикулярными,если угол между ними равен 90º;
Угол между двумя паралельными прямыми считается равным нулю;
Углом между плоскостью и не перпендикулярной ей прямой назывется угол межу этой прямой и ее проекцией на данную плоскость ( 0º );
);
Угол между взаимно перпендикулярными прямой и плоскостью равен 90º;
Если прямая параллельна плоскости( или лежит в ней) , то угол между ними считается равным 0º;
Двугранный угол, образованный двумя полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярно его ребру.величина двугранного угла принадлежит промежутку ( 0º ;180º);
В работе представлен способ решения стереометрических задач координатно- векторным методом. Замечу, что решение многих стереометрических задач вышеуказанным методом намного проще их решения средствами элементарной геометрии , при этом можно обойтись без дополнительных построений, которые затрудняют поиск решения задачи.
Рассмотрим решение некоторых аффинных задач (задачи на взаимное расположение прямых и плоскостей) и метрических задач (определение расстояния и углов между прямыми и плоскостями).
Для решения задач на взаимное расположение прямых и плоскостей и определения углов между прямыми и плоскостями в пространстве пользуются следующим учебным материалом:

Теоретические задачи.
угол между прямыми в пространстве есть острый угол между направляющими векторами данных прямых ( прямая однозначно задается точкой и направляющим вектором данной прямой);
угол между прямой и плоскостью определяется как угол между прямой и проекцией прямой на плоскость.Для нахождения этого угла используется угол между направляющим вектором прямой и вектором нормали
и вектором нормали  ( перпендикулярным ) плоскости
( перпендикулярным ) плоскости  ;
;
Расстояние от точки до прямой.
Задача 1.
Найдите расстояние от точки А ( 7;9;7) до прямой m заданной уравнениями :
х=2+4t , y=1+3t, z=2t.
Решение: так как плоскость  ┴ m и направляющий вектор прямой m
┴ m и направляющий вектор прямой m  есть вектор нормали плоскости
есть вектор нормали плоскости  , то составим уравнение плоскости, проходящей через точку А ( 7; 9; 7) :
, то составим уравнение плоскости, проходящей через точку А ( 7; 9; 7) :
4(x - 7)+3(y - 9)+2(z - 7)=0 ⟺ 4x+3y+2z - 69 =0. Составим систему уравнений , решив которую мы найдем координаты точки K пересечения прямой m и плоскости  :
:
После подстановки в первое уравнение системы переменных x ,y, z , выраженных через t , получим 4( 2+4t)+ 3( 1+3t) + 2 2t = 69 ⟺29t=58
2t = 69 ⟺29t=58 , тогда x=2+4· 2= 10, y=1+3 ·2=7, z=2 ·2=4 – искомые координаты точки К.Найдем расстояние между точками А и К( A ( 7; 9 ;7 ), K ( 10; 7 ;4) ) :AK = Таким образом,
, тогда x=2+4· 2= 10, y=1+3 ·2=7, z=2 ·2=4 – искомые координаты точки К.Найдем расстояние между точками А и К( A ( 7; 9 ;7 ), K ( 10; 7 ;4) ) :AK = Таким образом, =
= .
.
Ответ:  .
.
Задача 2.
В единичном кубе  найдите расстояние а) от точки
найдите расстояние а) от точки  до прямой
до прямой  ;б) от точки
;б) от точки  до прямой
до прямой ; в) от точки
; в) от точки  до прямой
до прямой  ; г) от точки
; г) от точки  до прямой
до прямой  .
.










 Решиние : введем систему координат Oxyz D1 C1
Решиние : введем систему координат Oxyz D1 C1





A1 B1
T




 D C
D C


A B
С помощью теоремы о трех перпендикулярах докажем перпедикулярность прямой  и плоскости
и плоскости  BO┴
BO┴  так как
так как  равносторонний
равносторонний  ┴ BO( медиана равносторонненго треугольника)
┴ BO( медиана равносторонненго треугольника)
 ┴
┴  ( диагонали основания) Составим уравнение прямой DB1 и проходящей через точку D(0; 0 ;0 ) : x= t ,y=t, z=t .Составим уравнение плоскости
( диагонали основания) Составим уравнение прямой DB1 и проходящей через точку D(0; 0 ;0 ) : x= t ,y=t, z=t .Составим уравнение плоскости  перпендикулярной прямой DB1 и проходящей через точку B (1; 1; 0) : (x- 1 ) + ( y- 1) + (z – 0 ) = 0⟺ x+y+z -2=0 .Решив систему уравнений, найдем координаты точки пересечения плоскости
перпендикулярной прямой DB1 и проходящей через точку B (1; 1; 0) : (x- 1 ) + ( y- 1) + (z – 0 ) = 0⟺ x+y+z -2=0 .Решив систему уравнений, найдем координаты точки пересечения плоскости  и прямой DB1 то есть точки Т:
и прямой DB1 то есть точки Т:
t+t+t-2 =0⟺ t= ⇒ T
⇒ T ⇒ AT= - искомое расстояние от точки А до прямой DB1.
⇒ AT= - искомое расстояние от точки А до прямой DB1.
Аналогично находятся расстояния из пунктов б, в и г.
Ответ : а)  .
.
Задача 3.
В правильной шестиугольной призме, все ребра которой равны 1. Найдите расстояние от точки B до прямой  .
.
Решение : составим уравнение плоскости  , проходящей через точку В и перпендикулярно прямой
, проходящей через точку В и перпендикулярно прямой  . Во введенной системе координат точки имеют координаты В С
. Во введенной системе координат точки имеют координаты В С









 В качестве вектора нормали плоскости
В качестве вектора нормали плоскости 
 z
z 




 Причем вектор .
Причем вектор . 





 Тогда плоскость
Тогда плоскость  задается уравнением E D T
задается уравнением E D T






 +⟺ F O C
+⟺ F O C
⟺  x+ y -2z -2=0 . A B
x+ y -2z -2=0 . A B
x
Обозначим точку пересечения плоскости  и прямую
и прямую  через Т, тогда
через Т, тогда
.Координаты точки Т найдем , решив систему уравнений , составленную из уравнения плоскости и прямой :
⟺⟺8t -1 =0⟺
⟺ . Координаты точки T . Таким образом,
. Координаты точки T . Таким образом,
== .
.
Ответ :  .
.
Задачи для самостоятельного решения
4. В системе координат Oxyz расположен единичный куб 
Координатным методом найдите расстояние до прямой AC1 от точки
а) А1 ; б) В1 ; в) С.
5. Правильная шестиугольная призма A…F1, все ребра которой равны 1 расположена так ,что ее центр основания совпадает с началом координат.
Координатным методом найдите расстояние от вершины В до прямой а) EF1 ;
б ) D1F1 ; в) C1D1.
Расстояние от точки до плоскости.
Задача 6.( Тренировочный вариант 166 от 09.10 .2016г.)
В прямоугольном параллелепипеде  точка М лежит на ребре
точка М лежит на ребре
DD1так, что DM:M  =1:2.Плоскость, проходящяя через точки A и М параллельно BD1, пересекает ребро CD в точке P .
=1:2.Плоскость, проходящяя через точки A и М параллельно BD1, пересекает ребро CD в точке P .
а) Докажите, что CP=DP .
б) Найдите расстояние от точки D1 до плоскости AMP , если известно, что AB=12, BC=9 и AA1=36.
 z
z
Решение:
C1 B1








D1 A1







M C B y


D P К A
Введем прямоугольную систему координат в пространстве так как по условию
AB=12, BC=9 и AA1=36 и DM:M  =1:2, то координты вершин паралелепипеда и точки М следующие : M( 12;0;12),
=1:2, то координты вершин паралелепипеда и точки М следующие : M( 12;0;12),
D ( 12; 0; 0) , A (12; 9; 0), B(0 ; 9 ; 0), C (0; 0; 0), D1 (12; 0; 36), A1(12; 9; 36),
B1 (0; 9; 36) , C1(0; 0; 36). Так как секущая плоскость параллельна диагонали BD1, то она содержит прямую MK параллельную ей. Рассмотрим подобные треугольники DD1B и MDK. DB =  ,диагональ BD1 параллелепипеда с измерениями 36, 9 и 12 равна 39. Из подобия треугольников DK=5.
,диагональ BD1 параллелепипеда с измерениями 36, 9 и 12 равна 39. Из подобия треугольников DK=5.
Рассмотрим прямоугольник ABCD AK и CD пересекаютя в точке P.Докажем, что CP= PD. Из подобия треугольников DPK и ABK следует .
ч. и т.д.
Найдем расстояние от точки D1 до плоскости AMP, причем точка P ( 6; 0; 0) .
Составим уравнение плоскости (AMP):
 6x- 4y - 3z – 36 = 0 – искомое уравнение плоскости и вектор нормали этой плоскости
6x- 4y - 3z – 36 = 0 – искомое уравнение плоскости и вектор нормали этой плоскости  .По формуле для расчета расстояния между точкой и плоскостью, имеем = =
.По формуле для расчета расстояния между точкой и плоскостью, имеем = = .
.
.
Задача 7. (ЕГЭ- 2016, 06.06.2016 г.)

В правильной четырехугольной пирамиде SABCD сторона основания AB= 16 ,а высота равна 4. На ребрах AB ,CD ,AS отмечены точки M, N и K соответственно, причем AM = DN = 4,AK = 3.Найдите расстояние от точки K до плоскости SBC. z













Решение: S


D


K N
A O C y
M B
Во введенной прямоугольной системе координат центр основания пирамиды совпадает с началом координат О( 0;0;0) вершины имеют координаты:
S( 0 ;0 ;4),A(0; - 8 0), B(8
0), B(8 ;0 ;0 ) ,C(0 ;8
;0 ;0 ) ,C(0 ;8 ;0)и D( 0 ;- 8
;0)и D( 0 ;- 8 ;0) .
;0) .
Определим координаты точки K По условию AK= 3 , то точка K делит отрезок AS в отношении
По условию AK= 3 , то точка K делит отрезок AS в отношении :
:
- координаты точки K, где координаты концов отрезка AS AK: KS= 3: 9=1: 3 (  SOA по теореме Пифагора SA =
SOA по теореме Пифагора SA =
Таким образом,  = 0 ; z=
= 0 ; z= =1⇒ K(0
=1⇒ K(0 1).
1).
Составим уравнение плоскости  , причем воспользуемся другим способом задания уравнения плоскости, отличным от предыдущего. Так как плоскость проходит через точки S ( 0 ;0 ;4), B(8
, причем воспользуемся другим способом задания уравнения плоскости, отличным от предыдущего. Так как плоскость проходит через точки S ( 0 ;0 ;4), B(8 ;0 ;0 )и C(0 ;8
;0 ;0 )и C(0 ;8 ;0) то подставив координаты точек в общее уравнение плоскости Ax+By + Cz + D = 0, получим систему из трех уравнений:
;0) то подставив координаты точек в общее уравнение плоскости Ax+By + Cz + D = 0, получим систему из трех уравнений:
⟺⟺
⟺=0- уравнение плоскости (SBC), вектор нормали к плоскости.
вектор нормали к плоскости.
Расстояние от точки K до плоскости  : ==
: == .
.
Ответ :  .
.
Угол между плоскостями.
Задача 8 .
В правильной четырехугольной призме со стороной основания 4 и высотой 7 на ребре АА1 взята точка М так, что АМ = 2. На ребре ВВ1 взята точка K так, что В1K= 2. Найдите угол между плоскостью D1MK и CC1D.
со стороной основания 4 и высотой 7 на ребре АА1 взята точка М так, что АМ = 2. На ребре ВВ1 взята точка K так, что В1K= 2. Найдите угол между плоскостью D1MK и CC1D.
Решение: построим сечение призмы плоскостью, проходящей через точки K, M и D1.
Поскольку секущая плоскость (D1MK) пересекает параллельные грани призмы (A1D1D) || (BB1C1), то ∆ A1MK ∆KB1H и по определению подобия треугольников выполняется отношение длин сходственных сторон
∆KB1H и по определению подобия треугольников выполняется отношение длин сходственных сторон

⟺ . Z






A1 D1




T

B1 M C1



K A D y

B C
x
Во введенной системе координат вершины призмы имеют следующие координаты: A(0 ;0 ;0 ), B( 0;4;0), C( 4;4;0), D(0;4;0) ,
A1(0; 7;0),B1(4;0;7),C1(4;4;7) ,M(0; 0; 2),D1(0; 4;7) K( 4 ;0 ;5 ).найдем координаты вектора нормали к плоскости (C1CD) и (D1MK). Любой вектор
(0 ;4; 0)  (C1CD).Чтобы найти координаты вектора нормали плоскости (D1MK), составим уравнение этой плоскости. Подставим координаты любых трех точек плоскости , не лежащих на одной прямой в общее уравнение плоскости Ax+By + Cz + D = 0:
(C1CD).Чтобы найти координаты вектора нормали плоскости (D1MK), составим уравнение этой плоскости. Подставим координаты любых трех точек плоскости , не лежащих на одной прямой в общее уравнение плоскости Ax+By + Cz + D = 0:
⟺⟺⟺
⟺ - - 3x- 5y+ 4z-8=0⟺ 3x+5y-4z+8=0 –уравнение плоскости (D1MK), где вектор нормали плоскости 
.
Ответ: 45°.
Расстояние между прямыми.
Большей частью в стереометрических задачах встречаютя задачи на нахождение расстояния между скрещивающимися прямыми . Используем следующий теоретический материал: расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной прямой до плоскости ,проходящей через вторую прямую параллельно первой прямой.
Задача 9. В системе координат Oxyz расположен единичный куб  . Найдите рассстояние между прямыми а)АВ1 и А1С1 ;
. Найдите рассстояние между прямыми а)АВ1 и А1С1 ;
б) ВD1 и B1C ; в) BD и B1M ( M – середина ребра AB).


Решение :Во введенной системе координат z






вершины куба будут иметь координаты 








а) найдем расстояние между прямыми





АВ1 и А 1С1. D С у

Для этого составим уравнение А М В
плоскости  , проходящей через АВ1 и параллельно прямой А 1С1.
, проходящей через АВ1 и параллельно прямой А 1С1.
Векторы  и
и  напрявляющие векторы прямых и векторы параллельные плоскости
напрявляющие векторы прямых и векторы параллельные плоскости  .Найдем координаты вектора нормали
.Найдем координаты вектора нормали  плоскости
плоскости  из условия перпедикулярности двух векторов :
из условия перпедикулярности двух векторов :
⟺ ⟺ a = b = -c.
Допустим, что c = -1, то a= b= 1.Уравнение плоскости, проходящей через точку A ( 1 ;0; 0 ) имеет вид: 1·(x-1)+1·(y-0)-1·( z-0) =0⟺ x+ y - z- 1 = 0.Расстояние между прямыми АВ1 и А 1С1.
.
Ответ : а)  ; б)
; б)  ; в)
; в) .
.
Используемая литература.
ЕГЭ – 2011.Математика. Задача С 2. Геометрия .Стереометрия.
под редакцией В.А. Смирнова , И.В. Ященко, разработано МИОО
Математика.ЕГЭ – 2013 Многогранники: типы задач и методы их решения.( типовые задания С2) авторы : Корянов А.Г., Прокофьев А.А.
Векторы и координаты как аппарат решения геометрических задач.10 -11 класс
Издательство « Дрофа» 2008г.
4. Геометрия 10. Авторы Е.В.Потоскуев, Л.И. Звавич
Издательство « Дрофа» 2010г.
5. Материалы с сайта http://alexlarin.net.
1� Е.В.Потоскуев. Векторы и координаты как аппарат решения геометрических задач..Элективные курсы 10- 11 классы.Учебное пособие. М.,издательство ДРОФА 2008г.





 );
); ;
; вектор нормали данной плоскости ;
вектор нормали данной плоскости ; ,
,
 ;
;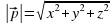 - длина вектора
- длина вектора  ;
;  длина вектора
длина вектора или длина отрезка AB ,если A
или длина отрезка AB ,если A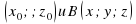
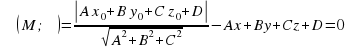 - уравнение плоскости
- уравнение плоскости  M(
M(
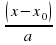 =
= - каноническое уравнение прямой, проходящей через точку M(
- каноническое уравнение прямой, проходящей через точку M( и направляющим вектором
и направляющим вектором  параллельно вектору
параллельно вектору
 – скалярное произведение векторов
– скалярное произведение векторов 










