Внутреннее представление вещественных чисел в стандарте IEEE754

Тема: " Внутреннее представление вещественных чисел в стандарте IEEE754".

Цель работы: 

Получение практических навыков представления вещественных чисел в двоичной системе счисления, перевод вещественных чисел из десятичной системы счисления в двоичную систему счисления.

Количество часов на выполнение работы

Продолжительность выполнения данной практической работы составляет 2 академических часа.

Оборудование

• тетрадь;

• ручка (карандаш);

• калькулятор.

Краткие теоретические сведения

При представлении вещественных чисел в любой системе счисления используют запись с плавающей точкой. Любое число в любой системе счисления можно представить в виде:

,

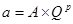где:

Q – основание системы счисления;

A – мантисса;

p – порядок.

Например в десятичной системе счисления число 3,14 можно представить в виде:

3,14=0,314*10¹

Здесь мантисса равна 0,314, а порядок равен 1.

Такое представление чисел далеко не однозначно. Число 3,14 можно представить как:

3,14=3,14*100=0,314*10¹=0,0314*10²=…

Порядок числа определяет положение запятой и записи мантиссы. При изменении порядка соответствующим образом меняется положение запятой. Запятая как бы «плавает». Это изменение запятой и дало название способу представления чисел.

Число с плавающей точкой представляется неоднозначно. Одно из этих представлений называется нормализованным. В этом случае для десятичной системы счисления мантисса должна удовлетворять требованию:

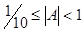
Другими словами, первая цифра мантиссы после запятой должна быть отличной нуля. Для числа 3,14 представление в нормализованной форме будет иметь следующий вид:

3,14=0,314*10¹

Здесь A=0,314, p=1. Аналогично для числа -0,00062 имеем -0,00062=0,62*10^-3 A=0,62, p=-3.

Точно также в любой системе счисления с основанием Q число a неравное нулю записывается в форме с плавающей точкой. Число a называется нормализованным, если выполняется условие:

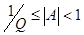
Дано A(10)=43,97. Найти A(2).

Сначала переводим целую часть B(10)=43

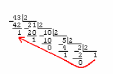
Рисунок 1 – Перевод целой части

B(2)=101011

Затем дробную C(10)=97

C(2)= 1100001

Записываем результат

D(2)= 101011,1100001

Теперь приводим число к нормализованному виду. Для этого сдвигаем запятую на шесть разрядов 6(10)= 110(2).

Получили мантиссу равную 0,1010111100001 и порядок равный 110.

Ответ:

A(2)=0,1010111100001*10¹¹⁰

Рассмотрим число 567.25 и переведем его в двоичную систему счисления.

Перевод целого числа из десятичной системы счисления в двоичную систему.

Целая часть числа равна 567. Будем последовательно делить это число, а затем частное на 2 до тех пор, пока это возможно, фиксируя при этом остаток от деления:

567:2 = 283 (остаток 1)

283:2 = 141 (остаток 1)

141:2 = 70 (остаток 1)

70:2 = 35 (остаток 0)

35:2 =17 (остаток 1)

17:2 = 8 (остаток 1)

8:2 = 4 (остаток 0)

4:2 = 2 (остаток 0)

2:2 = 1 (остаток 0)

Теперь запишем число, начиная с последнего частного, приписывая ему остатки в противоположном порядке. Получим

567₁₀ = 1000110111₂

Эти же операции можно записать последовательным делением в столбик:

Перевод дробной части вещественного числа из десятичной системы счисления в двоичную.

Дробную часть, а затем дробные части получающихся произведений следует последовательно умножать на 2 до тех пор, пока очередная дробная часть произведения не окажется равной нулю или не будет достигнута нужная точность дроби.

Целые части полученных произведений, записанные последовательно слева направо после запятой в искомом числе, образуют дробную часть искомого числа.

Переводим дробную часть числа:

0.25 * 2 = 0.50.

0.50 * 2 = 1.00 (дробная часть числа равна 0, стоп).

Записываем последовательно слева направо целые части полученных произведений

0.25₁₀ = 0.01₂

Таким образом

567,25₁₀ = 1000110111,01₂

Задания по практической работе

1. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 110100100₂ и 100011₂.

2. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 100110100₂ и 11100₂.

3. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 101111001₂ и 11101₂.

4. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 110111100₂ и 101100₂.

5. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 101101100₂ и 11010₂.

Контрольные вопросы

1. Что такое система счисления?

2. Какие системы счисления называются непозиционными?

3. Что такое основание, алфавит и базис системы счисления?

4. По каким правилам выполняется перевод вещественного числа из десятичной системы счисления в двоичную систему?