ГБПОУ «Починковский сельскохозяйственный техникум»
Утверждаю
Директор ГБПОУ ПСХТ
_________ А.А. Пузырев
«___» __________ 2024г.
Положение
о проведении общетехникумовской олимпиады
по дисциплине «Информатика»
с. Починки, 2024 г.
1.Общие положения
1.1. Настоящее Положение определяет цели и задачи общетехникумовской олимпиады по дисциплине «Информатика» среди обучающихся, порядок её проведения.
1.2. Олимпиада имеет статус общетехникумовской и проводится в соответствии с планом работы методиста на 2024-2025 учебный год.
1.3. Для проведения Олимпиады создаётся жюри из преподавателей техникума.
2. Цели и задачи Олимпиады:
2.1. повышение интереса обучающихся к изучению информатики;
2.2. мотивация обучающихся к углубленному изучению информатики;
2.3. создание оптимальных условий для выявления одаренных и талантливых обучающихся, с ориентацией на дальнейшее интеллектуальное развитие и профессиональную деятельность;
2.4. воспитание здорового духа конкурентной борьбы и стремления к победе.
3. Участники олимпиады
3.1. Участниками Олимпиады являются обучающиеся 1 курсов ГБПОУ ПСХТ.
4. Условия проведения Олимпиады
4.1. Олимпиада проводится 18 октября 2023 г. на базе ГБПОУ ПСХТ.
4.2. Олимпиада проводится в один этап:
общетехникумовский (решение задач) – 60 минут.
4.3. В процессе решения заданий участники не могут общаться.
4.4. Для выполнения заданий Олимпиады каждому участнику персональный компьютер или нетбук.
4.5. Во время олимпиады участникам запрещено пользоваться какими-либо средствами связи.
4.6. За нарушение правил Олимпиады участник, может быть дисквалифицирован.
4.7. Участник олимпиады обязан до истечения отведенного времени сдать свою работу. Участник может сдать работу досрочно, после чего должен покинуть место проведения Олимпиады.
4.8. Проверка заданий Олимпиады осуществляется в течение 1 суток после проведения.
5. Процедура оценивания выполненных заданий
5.1. Задания оцениваются балами в зависимости от сложности задания
5.3. Решение каждой задачи оценивается целым числом баллов.
5.4. Проверка работ осуществляется Жюри олимпиады согласно критерий оценивания для каждого задания:
Приложение 1.
Ведомость оценивания работ участников Олимпиады
| № п/п | Фамилия Имя Отчество | Количество баллов за задание | Итоговый балл | Рейтинг (место) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
| … |
|
|
|
|
|
|
|
|
|
|
|
6. Подведение итогов Олимпиады и награждение победителей.
6.1. Победители олимпиады определяются по сумме набранных баллов в личном зачете.
6.2. Обучающиеся, занявшие первые три места по сумме балов в Олимпиаде награждаются грамотами.
7. Задания Олимпиады
7.1. Олимпиадные задания предусматривают проверку теоретических знаний и практических умений, полученных на занятиях.
Приложение 2. Задание 1
В зале 11112 девочек и 11002мальчиков. Сколько обучающихся в зале?
(5 баллов)
Задание 2
Существует ли треугольник, длины сторон которого выражаются числами 128,1116, и 110122?
(10 баллов.)
Задание 3
Заполните пустые ячейки:
| 2–ая система счисления | 8-ая система счисления | 10-ая система счисления | 16-ая система счисления |
| 10011 |
|
|
|
|
| 233 |
|
|
|
|
| 46 |
|
|
|
|
| AF |
(12 баллов)
Задание 4
Разгадать числовые ребусы, записанные в двоичной системе счисления:
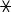
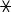
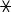

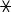

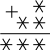
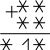
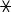
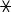
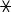

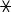
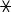
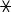

(4 по 3 балла)
Задание 5
Все файлы и каталоги на дисках организованы в виде дерева. Если бы перечисленные ниже термины являлись именами файлов с соответствующим имени содержанием, то как бы организовали структуру этих фалов на диске. Нарисуйте «Дерево» файлов и каталогов:
Один ноль манипулятор «Мышь» CD-ROM
Бейсик ноль сложение Семь
Монитор конъюнкция графопостроитель Сканер
Один клавиатура пять СИ
Звуковые колонки системный блок отрицание три
Четыре вычитание Ассемблер шесть
Умножение отрицание винчестер Паскаль
Деление джойстик эквиваленция дизъюнкция
Принтер следование два Дискета
(13 Баллов)
Задание 6
Составьте алгоритм решения следующей задачи. Как набрать из реки 7 литров воды, если имеются сосуды ёмкостью 3 и 8 литров?
(5 баллов)
Задание 7
Три свидетеля дали показания, что преступники скрылись с места преступления:
на чёрном «Бьюике»;
на синем «Форде»;
Не на чёрном «Крайслере»
Каждый из них в чём-то ошибался. На какой машине скрылись преступники?
(10 баллов)
Задание 8
Квадрат, ромб, круг и треугольник вырезаны из белой, синей, красной и зелёной бумаги. Известно, что круг не белый и не зелёный, синяя фигура лежит между ромбом и красной фигурой, треугольник не синий и не зелёный, квадрат лежит между треугольником и белой фигурой. Какая фигура вырезана из зелёной бумаги?
(10 баллов)
Ответы
Задание 1
1510+1210=2710 (5 баллов)
Задание 2
Такого треугольника не существует, т.к. 1010+1710=27
(10 баллов.)
Задание 3
Заполните пустые ячейки:
| 2–ая система счисления | 8-ая система счисления | 10-ая система счисления | 16-ая система счисления |
| 10011 | 23 | 19 | 13 |
| 10011011 | 233 | 155 | 9В |
| 101110 | 56 | 46 | 2Е |
| 10101111 | 257 | 175 | AF |
(12 баллов)
Задание 4
Разгадать числовые ребусы, записанные в двоичной системе счисления:
| + |
| 1 |
|
| + | 1 | 1 |
|
| — | 1 | 1 |
|
| — | 1 | 0 | 0 |
| 1 | 1 |
| 1 | 1 |
|
| 1 | 0 |
|
|
| 1 | 1 |
| 1 | 0 | 0 |
|
| 1 | 1 | 0 |
|
|
|
| 1 |
|
|
|
|
| 1 |
(4 по 3 балла)
Задание 5
В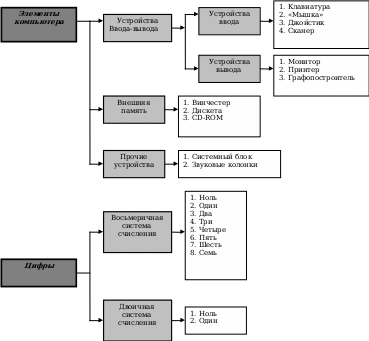 се файлы и каталоги на дисках организованы в виде дерева. Если бы перечисленные ниже термины являлись именами файлов с соответствующим имени содержанием, то как бы организовали структуру этих фалов на диске. Нарисуйте «Дерево» файлов и каталогов:
се файлы и каталоги на дисках организованы в виде дерева. Если бы перечисленные ниже термины являлись именами файлов с соответствующим имени содержанием, то как бы организовали структуру этих фалов на диске. Нарисуйте «Дерево» файлов и каталогов:
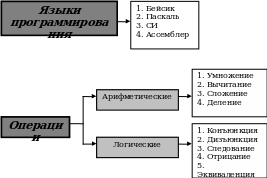
(13 Баллов)
Задание 6
| I способ | II способ |
| 3 литра | 8 литров | 3 литра | 8 литров |
| 3 | 0 | 0 | 8 |
| 0 | 3 | 3 | 5 |
| 3 | 3 | 0 | 5 |
| 0 | 6 | 3 | 2 |
| 3 | 6 | 0 | 2 |
| 1 | 8 | 2 | 0 |
| 1 | 0 | 2 | 8 |
| 0 | 1 | 3 | 7 |
| 3 | 1 |
|
|
| 0 | 4 |
|
|
| 3 | 4 |
|
|
| 0 | 7 |
|
|
(5 баллов)
Задание 7
Ответ: Синий «Бьюик»
Решение:
С – чёрный,
S – синий.
В – «Бьюик»,
F- «Форд»,
К – «Крайслер».
Ложные высказывания: 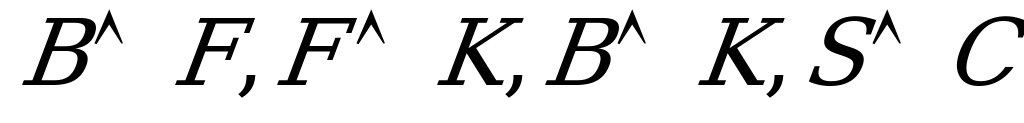
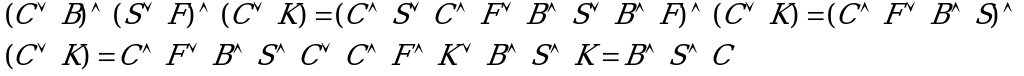
(10 баллов)
Задание 8
Ответ: Квадрат
Используя условия задачи для решения лучше всего воспользоваться следующей таблицей:
|
| Белый | Синий | Красный | Чёрный |
| Круг | 0 | 1 | 1 | 0 |
| Квадрат | 0 | 1 | 1 | 1 |
| Ромб | 1 | 0 | 0 | 1 |
| Треугольник | 0 | 0 | 1 | 0 |
Рассуждения: Из таблицы видно, что треугольник – красный, следовательно, получается следующая таблица:
|
| Белый | Синий | Красный | Чёрный |
| Круг | 0 | 1 | 0 | 0 |
| Квадрат | 0 | 1 | 0 | 1 |
| Ромб | 1 | 0 | 0 | 1 |
| Треугольник | 0 | 0 | 1 | 0 |
Из таблицы видно, что круг – синий. Т. к. квадрат из таблицы синий или зелёный, но из предыдущего высказывания следует, что он не может быть синим, следовательно, квадрат – зелёный.
(10 баллов)
Положение разработал:
Преподаватель ООД Хоршев Р.А.______________________/Хоршев Р.А./







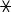


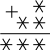
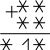
 се файлы и каталоги на дисках организованы в виде дерева. Если бы перечисленные ниже термины являлись именами файлов с соответствующим имени содержанием, то как бы организовали структуру этих фалов на диске. Нарисуйте «Дерево» файлов и каталогов:
се файлы и каталоги на дисках организованы в виде дерева. Если бы перечисленные ниже термины являлись именами файлов с соответствующим имени содержанием, то как бы организовали структуру этих фалов на диске. Нарисуйте «Дерево» файлов и каталогов:










