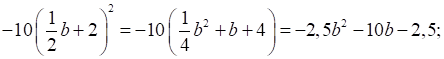Технологическая карта урока
Ф.И.О. учителя: Тагирова Брият Чираговна
| Дата | |
| Предмет | алгебра |
| Класс | 7 |
| Тип урока | Открытие нового знания |
| Технология построения урока | Системно-деятельностный подход |
| Тема | Возведение в квадрат суммы и разности двух выражений |
| Цель | Создать условия для развития умений возводить в квадрат суммы и разности двух выражений по формулам сокращенного умножения |
| Основные термины, понятия | выражение, квадрат разности двух выражений, квадрат суммы двух выражений, тождество, тождественное преобразование (преобразование), множитель, многочлен, понимает формулировку заданий: “упростить выражение”, “найти значение выражения” |
Задачи урока:
o Образовательная: формировать у учащихся умение возведения в квадрат и в куб суммы и разности двух выражений, учить учащихся видеть формулы сокращённого выражения и уметь их применять на практике (квадрат и куб разности, квадрат и куб суммы).
o Развивающая: развитие логического, аналитического, алгоритмического мышлений учащихся; внимания, памяти, математической зоркости.
o Воспитательная: воспитывать усидчивость, аккуратность, самостоятельность, интерес к предмету.
Планируемые результаты
Предметные:Познакомятся с основными формулами сокращенного умножения: квадрата суммы и квадрата разности двух выражений; научатся применять данные формулы при решении упражнений
Метапредметные:
Личностные УУД: формировать интерес к изучению темы и желание применять приобретенные знания и умения
Регулятивные УУД: уметь определять и формулировать цель урока; давать оценку своим личностным качествам и чертам характера, определять направление своего развития
Познавательные УУД: уметь отличать новое от уже известного; уметь осознанно и произвольно строить речевое высказывание; самостоятельно создавать алгоритм деятельности; использовать знаково-символические средства; строить логическую цепочку рассуждений
Коммуникативные УУД: учится критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его
Оборудование:
учебник Ю. Н. Макарычев и др. «Алгебра. 7 класс»
рабочая тетрадь по алгебре
черновик
доска, с меловыми записями
Основные понятия: квадрат суммы, квадрат разности, куб суммы, куб разности, формулы сокращённого умножения, многочлен.
Организационная структура урока
1. Организационное начало урока (2 мин)
2. Целеполагание (активизация учащихся) (1 мин)
3. Актуализация знаний (7 мин)
4. Основная часть урока (30 мин)
5. Подведение итогов урока (3 мин)
6. Рефлексия (2 мин)
Список литературы: учебник Ю. Н. Макарычев и др. «Алгебра. 7 класс»
Ход урока
I Организационный момент
Учитель: Здравствуйте, ребята!
«Знание только тогда знание, когда оно приобретено усилиями своей мысли».
(Л.Н.Толстой )
- Как вы понимаете эти слова?
- Сегодня мы продолжим изучение темы «Умножение многочлена на многочлен». Еще в глубокой древности было подмечено, что некоторые многочлены можно умножать короче, быстрее, чем все остальные.
Так появились формулы сокращенного умножения. Их несколько. Сегодня нам предстоит сыграть в роли исследователей и «открыть» две из этих формул – квадрата суммы и квадрата разности.
- Запишите число и тему урока: « Квадрат суммы. Квадрат разности».
II Актуализация знаний
Устная работа.
1. Выполните возведение в степень.
а) (–2х)2; в) 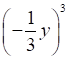 ; д) (–7х3у2)2;
; д) (–7х3у2)2;
б) (5а2)2; г) 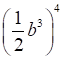 ; е) (–0,6п4т5)2.
; е) (–0,6п4т5)2.
2. Выполните умножение.
а) 2х2 · 3х7; в) 3а (2а2 – 5а); д) (х – 3) (у + 4);
б) 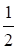 y5 · (–4y3); г) –2x4
y5 · (–4y3); г) –2x4 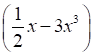 ; е) (2a – 1) (b – 5).
; е) (2a – 1) (b – 5).
Объяснение нового материала.
Объяснение нового материала следует производить в несколько этапов. 1. представить выражение (a + b)2 в виде многочлена.
(a + b)2 = (a + b) (a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2.
Аналогично возводится в квадрат выражение a – b:
(a – b)2 = (a – b) (a – b) = a2 – ab – ab + b2 = a2 – 2ab + b2.
2 полученные тождества называются формулами квадрата суммы и разности двух выражений. Они нужны, чтобы сделать проще преобразования.
3. Разобрать примеры 1 и 2 из учебника. Остальные примеры приводить пока не нужно
III. Формирование умений и навыков.
1. № 799.
2. № 803.
решение:
(Во избежание ошибок следует вести подробные записи.)
а) (2x + 3)2 = (2x2) + 2 · 2x · 3 + 32 = 4x2 + 12x + 9;
д) 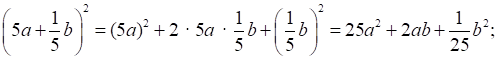
е) 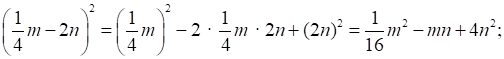
з) (10с + 0,1у)2 = (10с)2 + 2 · 10с · 0,1у + (0,1у)2 = 100с2 + 2су + 0,01у2.
3. № 812.
Решение:
а) (а2 – 3а)2 = (а2)2 – 2а2 · 3а + (3а)2 = а4 – 6а3 + 9а2;
б) 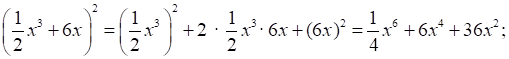
в) 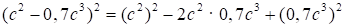 = c4 – 1,4c5 + 0,49c6;
= c4 – 1,4c5 + 0,49c6;
г) 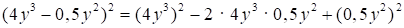 = 16y6 – 4y5 +
= 16y6 – 4y5 +
+ 0,25y4;
д) 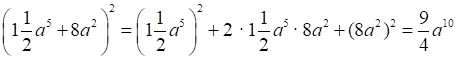 + 24a7 +
+ 24a7 +
+ 64a4;
е)  = 0,36b2 – 72b3 +
= 0,36b2 – 72b3 +
+ 3600b4.
№ 819.
Решение:
| а) (х – 6)2 – х (х + 8) = 2; х2 – 12х + 36 – х2 – 8х = 2; –20х = –34; х = 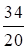 ; ; х = 1,7. | б) 9х (х + 6) – (3х + 1)2 = 1; 9х2 + 54х – 9х2 – 6х – 1 = 1; 48х = 2; х = 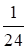 . . |
| Ответ: 1,7. | Ответ: 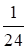 . . |
| в) у (у – 1) – (у – 5)2 = 2; у2 – у – у2 + 10у – 25 = 2; 9у = 27; у = 3. | г) 16у (2 – у) + (4у – 5)2 = 0; 32у – 16у2 + 16у2 – 40у + 25 = 0; –8у = –25; у = 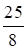 . . |
| Ответ: 3. | Ответ: 3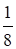 . . |
4. № 821.
При решении этого номера учащимся предстоит выполнять более сложные преобразования. Зачастую они делают очень распространенную ошибку: сначала умножают число на выражение в скобках, а потом результат возводят в квадрат.
Необходимо напомнить учащимся, что действие возведения в степень является приоритетным среди всех остальных, поэтому его выполняют в первую очередь.
Решение:
а) 7 (4а – 1)2 = 7 (16а2 – 8а + 1) = 112а2 – 56а + 7;
в) 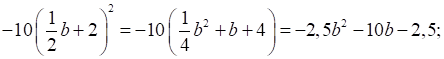
д) 9с2 – 4 + 6 (с – 2)2 = 9с2 – 4 + 6 (с2 – 4с + 4) = 9с2 – 4 + 6с2 – 24с +
+ 24 = 15с2 – 24с + 20.
5. № 823 (а, в).
Решение:
а) 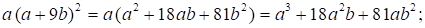
в) 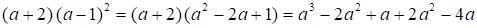 + 2 =
+ 2 =
= a3 – 3a + 2.
IV. Самостоятельная работа (с самопроверкой) Представьте в виде многочлена:
| 1. (х-2) ² |
| 2. (у-3) ² |
| 3. (4+х) ² |
| 4. (3-у) ² |
| 5. (-х-7) ² |
| 6. (-5-а) ² |
| 7. (2х-у) ² |
Ответы:
| 4х²-4ху+у² | 25+10а+а² | у²-6у+9 | 16+8х+х² | х²-4х+4 | х²+14х+49 |
| Ц | Е | О | Л | М | Д |
(получившееся слово: молодец)
1. (а + 2b)2
2. (3m + 4c)2
3. (5d – 3c)2
4. (2r – 4x)2
5. (3x + 2y)2
Обсуждение ошибок, допущенных учащими
V Домашнее задание.
П 32, доказать геометрический смысл
формулы (а - в) 2;
№ 805 (а, б), 810 (а-г).
VI Подведение итогов.
-С какими формулами мы познакомились сегодня на уроке?
Ребята.На уроке мы познакомились с новыми формулами - одними из формул сокращенного умножения:
-Чему равен квадрат суммы двух выражений?
-Чему равен квадрат разности двух выражений?
-Как вы думаете, зачем нужны нам эти формулы и стоит ли их запоминать?
Ребята. Эти формулы позволяют сократить время на вычисление квадрата суммы и разности двух выражений.
Понравился ли вам урок?
VII. Рефлексия
Я, в свою очередь, хочу сказать спасибо вам, ребята, за вашу активную работу на сегодняшнем уроке, думаю, что вы легко сможете применять все изученное в жизни.






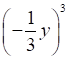 ; д) (–7х3у2)2;
; д) (–7х3у2)2;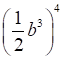 ; е) (–0,6п4т5)2.
; е) (–0,6п4т5)2.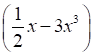 ; е) (2a – 1) (b – 5).
; е) (2a – 1) (b – 5).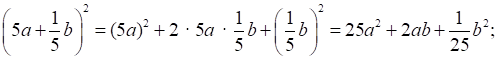
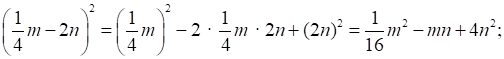
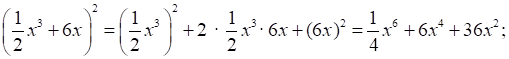
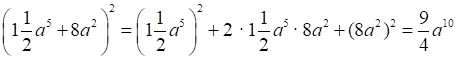 + 24a7 +
+ 24a7 +