Возвратные последовательности и рекурсивные фуркции

Рекурсивные функции

Под рекурсией понимают метод определения функции через её предыдущее и ранее определенное значение, а так же способ организации вычислений, при котором функция вызывает сама себя с другим аргументом. Основной задачей исследования рекурсивно заданных функций является получение f(n) в явной или «замкнутой» форме, т.е. в виде аналитически заданной функции.

Примеры рекурсивного задания функций

1. Методы решения рекурсивных соотношений

а) Метод индукции в том, что б снач угад реш, а затем дока его правильн по индукции. Пример:

f(0)=1 f(n+1)=2*f(n) Предположение: f(n)=

Базис: если f(n)= , то f(0)=1, что выполнено по определению.

Индукция: Пусть f(n)= , тогда для n+1 f(n+1)= 2 * =

Заметим, что базис сущес влияет на реш, так, например: Если f(0)=0, то f(n)=0;

если f(0)=1/7, то f(n)=(1/7)*; если f(0)=1/64, то f(n)=(2)

б) Метод итерации (подстановки) Суть метода в послед подст – итерации рекурс определения, с послед выявл общих закономерностей:

Пусть f(n)=3*f(n/4)+n, тогда:

f(n)=n+3*f(n/4)=n+3*[n/4+3*f(n/16)]=n+3*[n/4+3{n/16+3*f(n/64) }], и раскр скобки, получ:

f(n)=n+3*n/4+9*n/16+27*n/64+…+ *n/

Остановка рекурсии произойдет при , в этом сл последнее слагаемое не больше, чем

, то окончательно:

Совместная рекурсия. Пусть две одноместные функции f и g заданы соотношениями:

f(0) = a, g(0) = b, f(n+1) = F(n,f(n),g(n)), g(n+1) = G(n,f(n),g(n)),

где a и b нек числа, а функции F и G примитивно рекурсивн функции трех арг. Покажем, что тогда функции f и g примитивно рекурсивны.

Возвратная рекурсия. при рекурсивном определ м использ не только знач в предыдущей точке, но и любое предшествующее значение.

Теор Пусть функция g 1 аргум примитивно рекурсивна, причем g(x) при x0 ; пусть F примит рекурс функция 2 аргум; пусть c произв конст. Тогда функция h, заданная соотношением

h(0) = c, h(x) = F(x,h(g(x))) при x0

примитивно рекурсивна.

Определение возвратной последовательности

Последовательность может быть определена:
  1) формулой для общего члена посл-ти a_n = (n);
  2) рекуррентн соотн. При этом зад неск 1х членов посл-ти и ф-лы, позв послед шаг за шагом, опр любой член посл-ти. Таким образом, заданные последовательности называют еще возвратными последовательностями.

Например, геометрическую прогрессию x₁ ,  x₂ , … x_n , …можно зад,ать как с помощью ф-лы общего члена x_n = b₁q ^{n – 1},       n = 1, 2, 3, … , так и рекуррентной ф-лой

x₁ = b₁;       x_n = q x_{n – 1},       n = 2, 3, …

a_n = a₀ + d(n-1) –арифметическая прогрессия

Напр, зад 2 первых члена посл-ти а₁, а₂ и ур (a_n-2, a_n-1, a_n) = 0. Тогда, полагая п = 3, м составить ур для а3: (a₁, а₂, а₃) = 0, из кот найти a₃. Далее, полаг п = 4, из ур (a₂, a₃, a₄)= 0 находится а4 и т.д.

Формальную сумму, составленную из элементов данной посл-ти an, называют рядом, а слагаемые с номером п (общий член посл-ти) называют общим членом ряда.

Ряд записывают в виде а₁+а₂+а₃+ ... 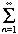+a_n+ ...a_n
определяем частичные суммы: S₁ = а₁, S₂ = а₁+а₂, S₃ = а₁+а₂ +а₃, — и т.д.
  Посл-ть частичных сумм Sn ест опр в виде рекурр соотн:
S₀ = 0,   S_n = S_n-1 + a_n   ( n = 1, 2, 3 ... ) или S₁ = а₁,   S_n = S_n-1 + a_n   ( n = 2, 3, 4 ... )

Пусть u₁, u₂, u₃, . . . , u_n, . . . , - возвр посл-ть порядка k, члены кот удовл ур:

u_{n + k} == a₁u_{n +k – 1} + a₂u_{n + k – 2} + … + a_ku_n (n m). Посл-ть сумм S₁ = u_1,

S₂ = u₁ + u₂ , . . . , S_n = u₁ + u₂ + . . . + u_n, . . . также возвратна и удовл ур

S_{n + 1 + k} = (1 + a₁) S_{n + k} + (a₂ - a₁) S_{n + k - 1} + . . . + (a_k – a_{k - 1}) S_{n + 1} - a_kS_n

Т к члены {u_n} удовл ур вида u_{n + 1} = q u_n , то члены {S_n} д удовл ур S_n (1 + q) S_{n + 1} - q S

Б)Посл-ть квадр нат чисел.

Здесь u_n = n² и S_n = 1 + 2² + . . . + n² . Т к члены {u_n} удовл ур u_{n + 3} = 3u_{n + 2} - 3u_{n + 1} + u_n ,

то члены {S_n} удовл ур вида S_{n + 4} = 4S_{n + 3} - 6u_{n + 2} + 4S_{n + 1} - S_n .

Прим. Подобрать формулу для общего члена ряда

10)1/2•1 + 1/2•2 + 1/2•3 + 1/2•4 + 1/2•5 + ... , 11)1 + 1/2 + 1•2/4 + 1•2•3/8 + 1•2•3•4/16 + ... ,

12)1 + 1/4 + 1/12 + 1/32 + 1/80 + ...Отв.

Опр. . Возвратной (рекуррентной) посл-тью порядка r называют последовательность, для зад кот треб зад 1е её r членов, т.е. числаx₁ ,  x₂ , … x_k , а ост члены  посл-ти опред с пом рекур ф=лы (рекур ур) n k , где q₁ ,  q₂ , … q_k ,– зад числа (коэфф рекуррентной формулы). 

Замечание 1. Числа x₁ ,  x₂ , … x_k ,наз нач усл.

Примеры

1 последовательность квадратов натуральных чисел: u₁ = 1², u₂ = 2², u₃ = 3², . . . , u_n = n², . . .

Здесь u_{n + 1} = (n + 1)² = n² + 2n + 1 т е , u_{n + 1} = u_n + 2n + 1. Увеличивая n на , получим:

u_{n + 2} = (n + 2)² = n² + 4n + 4 = (n² + 2n + 1) + 2n + 3 = u_{n + 1} + 2n + 3. u_{n + 2} = u_{n + 1} + 2n + 1

Вычитая почленно (1) из (2), получим:

u_{n + 2} - u_{n + 1} = (u_{n + 1} + 2n + 3) – (u_{n + 1} = u_n + 2n +1) = u_{n + 1} - u_n+2,u_{n + 2} = 2u_{n + 1} - u_n +2.

Увеличивая в равенстве (3) n на 1, будем иметь:

u_{n + 3} = (n +3)² = n² + 6n + 9 = (n² + 4n +4) + 2n +5 = u_{n + 2} + 2n +5,u_{n + 3} = u_{n + 2} + 2n + 5.

Вычитая почленно (2) из (4), получим:

u_{n + 3} - u_{n + 2} =(u_{n + 2} +2n +5) – (u_{n + 1} + 2n + 3) = u_{n + 2} - u_{n + 1} +2,u_{n + 3} = 2u_{n + 2} - u_{n + 1}+2,

Вычитая почленно (3) из (5), получим:

u_{n + 3} - u_{n + 2} = (2u_{n + 2} - u_{n + 1} + 2) – (2u_{n + 1} - u_n + 2) = 2u_{n + 2} - 3u_{n + 1} + u_n ,

или u_{n + 3} = 3u_{n + 2} - 3u_{n + 1} + u_n.. (6)

Получили возвратное уравнение 3 порядка, т. е. k = 3, a₁ = 3, a₂ = -3, a₃ = 1.

Производящая функция посл-ти -

Многочлен м рассм как производящ функц посл-ти

Рассмотрим производящую функцию произведения функций . Коэф-т   при  и  определен соотнощением

 и=0.

То есть многочлен  имеет степень самое больш  r-1, значит степень числителя функции   меньше степени знаменателя.

Характеристическое уравнение

Характеристический многочлен линейного рекуррентного уравнения – многочлен  

Характеристический многочлен  и многочлен   связаны меж собой соотношением

Прим. r=2 или можно с пом числа λ, при кот посл-ть вида удовл рек ф-ле (1) тогда подст в (1) возн ур (4)

Общее решение рекуррентного уравн 2 порядка

 1) 2различных вещественных корня  λ₁ и  λ₂ , каждая из посл-тей и удовлетворяет рекуррентной ф=ле (1), т.е для любых чисел c₁ и c₂ посл-ть с общ членомтакже удовлетворяет рекуррентной ф-ле (1).c₁ и c₂ наз произв пост.

2) 2 совпавших вещественных корня  λ₁ = λ₂, проверкой показывается, что каждая из посл-тей и удовлетворяет рекуррентной ф-ле (1), поэтому для любых чисел c₁ и c₂ посл-ть с общим членом также удовлетворяет рекуррентной формуле (1).

3) 2 комплексно-сопряженных корня   λ_{1, 2} = α ± i β,  каждая из посл-тей

и

удовлетворяет рекуррентной ф=ле (1), поэтому для любых чисел c₁ и c₂ посл-ть с общим членом

также удовлетворяет рекуррентной ф-ле (1).

Пр1 c граничными условиями

Пр3. Найти ф-лу общего члена посл-ти, заданной рекуррентной формулой

с нач усл

    Реш. Б действ в соотв со схемой Характ уравнение для этой посл-ти имеет вид

его корни:

1. Поск хар ур имеет 2 компл сопряж корня, то общее реш рекурр ур (7) имеет вид

,c₁ и c₂ - произв вещ .

1. Найдем теперь зн произв пост c₁ и c₂ так, чтобы для посл-ти

2. вып нач усл (8). Это озн, что числа c₁ и c₂ д удовл след с-ме из 2 лин уравн с 2 неизвест:

4. Для того, чтобы решить эту систему ур, перепишем её в следующем виде:

1. Подст найд зн произв пост c₁ и c₂ в (9), получ иск ф-лу общего члена посл-ти:

Прим.4

Гармонические последовательности

Числовые посл-ти Фибоначчи и Люка явл прим гармонич посл-тей. Конст посл-тей Фибоначчи и Люка или их числ инвар явл золотая пропорция (Ф=1,618033). Интерес к золотой пропор и числам Фибоначчи и Люка порожд не только тем, что с ними связ целые обл в культуре и науке, но в боль степени тем, что они очень часто встреч во мн явл ок мира. Поэтому важно выясн к каким обобщ классам посл-тей отн числа Фибоначчи и Люка, и как связаны числ инварианты других посл-тей с золотой пропорцией. Нек посл-ти Люка носят собственные имена:

— числа Фибоначчи — числа Люка

— числа Пелля (англ.) — числа Пелля—Люка (англ.)

числа Мерсенна числа Ферма числа Якобшталя 

Явные ф-лыХарактерист многочл посл-тей Люка и явл:

Его дискр предп не-0. Корни характ многочл и м использ для получ явных формул:

и

2. Гармонические посл-ти с рекуррентным свойством: a(n)=ka(n-1)+a(n-2)

Рассм посл-ти вида: .При k=1 получим рекурр ф-лу:.

Эта рекурр ф-ла при a(0) = 1, a(1)=1 порож числа Фибоначчи: Ф(n) = 1, 1, 2, 3, 5, 8, 13… При a(0) =2 и при a(1)=1 ф-ла порожд числа Люка: L(n)= 2, 1, 3, 4, 7, 11…Для этих посл-тей отн соседн членов стрем в пред к зол пропорц: Число Ф явл числ инвар или конст этих посл-тей. Число Ф единств положит число, кот перех в обр ему при вычит 1. Обр вел числа Ф в точн= числу, стоящ после зпт. Конст этого сем посл-тей явл корнем уравн вида: X₁–1/X₁=1.

При k=2 получим рекурр формулу: Эта рекур ф-ла при a(0) = 2 и при a(1)=2 порож гл посл-ть вида: K₂(n) = 2, 2, 6, 14, 34, 82, 198… В энц Нейла Слоуна эта посл-ть зареги под ном A002203 [1].Для посл-тей этого класса: Число X₂ явл числ инвар или конст этого сем посл-тей. Число X₂ обл особ св-вом - оно пере в обр ему при вычит целой части. Обр вел числа X₂ в точн= числу, стоящ после запятой. В этом число X₂ проявл сходство с золотой пропорцией. Конст этого семе посл-тей явл корнем ур вида: X₂–1/X₂=2. У всякой посл-ти с рекур свойством a(n) = 2a(n-1) + a(n-2) с любыми нач членами отн соседних членов по мере удал от начала стрем к X₂=2,41421356…

При k=3 получ рек ф-лу: Эта рекур ф=ла при a(0) = 2 и при a(1)=3 порождает главную посл-ть вида: K₃(n) = 2, 3, 11, 36, 119, 393, 1298… В энц Нейла Слоуна эта посл-ть зарег под ном A006497 [1].Для посл-тей этого класса:

Число X₃ явл числ инвар или конст этих посл-тей. Число X₃ перех в обратное ему при вычит целой части. Обратная вел числа X₃ в точн= числу, стоящему после запятой. Конст этого семе посл-тей явля корнем уравн вида: X₃–1/X₃=3.

При k=8 получим рек формулу:

Эта рекурр формула при a(0) = 2 и при a(1)=8 порож главную посл-ть вида: K₈(n) = 2, 8, 66… В энц Нейла Слоуна эта посл-ть зарег под номером A086594 [1]. Для посл-тей этого класса:

Число X₈ явл числ инвар или конст этих посл-тей. Число X₈ перех в обратное ему при вычит целой части. Обр вел числа X₈ в точн равна числу, стоящ после зпт. Конс этого сем посл-тей явл корнем ур вида: X₈–1/X₈=8.

Ур X–1/X= k позв получить для посл-тей, имеющих рекурр соотн a(n) = ka(n-1) + a(n-2), большое семейство числовых инвар, близких по св-вам к золотой пропорции. Прим чисел со свойствами, близкими к свойствам золотой пропорции, явл: X₂ = 2,414213562…, X₃ = 3,302775637…, X₄ = 4,23606…, X₅ = 5,192582403…, X₁₁ = 11,0901… Их обр зн дают числа, стоящие после запятой: 1/X₂ = 0,414213562…, 1/X₃ = 0,302775637…, 1/X₄ = 0,23606…, 1/X₅ = 0,192582403…, 1/X₁₁ = 0,0901…

Прим:

А)Геом прогр. возвр посл-ть 1 порядка

Б)арифм прогр возвр посл-ть 2 порядка

В)посл-ть Фибоначчи возвр посл-ть 2 порядка

Геометрическое изображение

- определит Вронского

Г.м.т. пар точек

В зависимости от при гипербола, при пара прямых,

,эллипс.Оси-биссектрисы корд узлов

При C=-4 получим посл-ть 0, 2, 2, 0, −2, −2, 0, 2, ..

Примеры.задач

1.Посл-ть задана рекуррентно Найти общий член ряда

2. Посл-ть задана рекурр Док.по индукции что общий член посл-ти вычи по ф-ле

3. . Посл-ть задана рекурр при n2, Док.по индукции что общий член посл-ти вычисляется по ф-ле

4. Найти 1987-й член посл-ти

5. Пусть Выразить и через и .

6. Дана посл-ть : Выяснить, при каких зн явл периодической.

7. Дана посл-ть :

Выяснить, сущ ли такие положит и , что явл периодич.

8. Решить рекурр соотн а) Б)

арифметико-геометрические посл-ти

Выведите ф-лу общего члена и суммы первых n членов след рекурр посл-ти  x_n+1 = a· x_n + b (такая посл-ть наз арифметико-геометрической).

3.Рассм посл-ть {r_n}, удовл соотн r_n+2 = 5 · r_n+1−6 · r_n  (наз это соотн (1)).

a)Док, что для любого числа α посл-ть {α·r_n} также удовл этому соотн;

b)Док, что если 2 посл-ти {r_n} и {s_n} удовл (1), то и посл-ть {r_n + s_n} ему также удовл;

c)Найдите геом прогрессию, удовл соотн (1). Ск разлих таких прогрессий?

d)Исп рез предыд п этой задачи, напиш ф-лу с 2 произв парам c₁ и c₂, явл ф-лой n-го члена для посл-тей, удовл (1);

e)Док, что ваша ф-ла исчерп все посл-ти, удовл (1) (обр вн, что каждая такая посл-ть однозначно зад своими 2 первыми членами).

4.Продел анал опер и найд ф-лу n-го члена посл-ти Фибоначчи: F₁ = F₂ = 1, F_n+2 = F_n+1 + x_n..Получ явная ф-ла для чисел Фибоначчи наз ф-лой Бине. Не верится, что она задает целочисл посл-ть, но это так. Впр, если всп про бином Ньютона, то это стан очев. Док целочисл этой формулы при каждом нат n через бином Ньютона.

Напом: Под биномом Ньютона поним следующая формула:

6.На 1й клетке полоски 1×n стоит шашка. За 1 ход разреш передв шашку вправо на 1 или 2 клетки. Обозн через  f_n число разл способов перемест шашку из 1й клетки в n-ую. Найдите реккурентную зависимость f_n от f_{n − 1} и f_{n − 2}.

7.Найдите сумму n чисел 1 + 11 + 111 + ... + 11...11.

8.Сколькими способами можно разбить число N на слагаемых, каждое из кот равно одному из натуральных чисел 1, 2, 3, ..., n? Порядок слагаемых не важен.

8.Посл-ть {a_n}, сост из нат чисел, такова, что a₁  a₀ и a_n+1 = 3·a_n − 2·a_n−1. Док, что a₁₀₀ ≥ 2¹⁰⁰.

9.Дана посл-ть {x_n}. Изв x₁ = x₂₀₁₀ = 2010 и x_n = −x_n−1 + 2·x_n−2. Док, что x_n = 2010 для всяк n.

10.Найдите колич способов раскр полоску 1×n в три цвета: красный, синий и зеленый — так, что за красным цветом не следует зеленый (но при этом м ему предшеств).

Посл-ть () явл периодической (пров). При каких числах k и l посл=ть получается периодической? Какой длины может быть период?