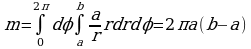Просмотр содержимого документа
«Вычисление массы плоской материальной фигуры»
ББК 22.21
ВЫЧИСЛЕНИЕ МАССЫ ПЛОСКОЙ МАТЕРИАЛЬНОЙ ФИГУРЫ
А.С. Тирский, старший преподаватель кафедры
«Естетственных и технических наук»,
Л.С. Толмачева., студентка группы Мех 09
Олёкминский филиал
ФГБОУ ВПО Якутская ГСХА»,, г. Олёкминск
Как известно, математика все больше и больше внедряет свои методы в технические науки. Целью такого внедрения является оптимизация решения данной задачи. Кроме того, зачастую решить задачу можно только математически. Рассмотрим одну из таких задач механики «Вычисление массы материальной фигуры»
Рассмотрим некоторую плоскую материальную фигуру Д. Геометрически будем считать эту фигуру квадрируемой замкнутую ограниченной областью. Поставим задачу вычисления массы такой фигуры. Если эта фигура однородна, а 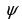 - ее плотность , то вычисление массы производится непосредственно:
- ее плотность , то вычисление массы производится непосредственно: 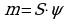 ,где S-площадь фигуры.
,где S-площадь фигуры.
Предположим теперь, что данная плоская фигура не является однородной.Для определения массы фигуры, будем теперь ее рассматривать в системе координат. Если взять произвольно точку фигуры Р(х,у), то плотность 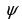 в этой точке будет зависеть от координат точки, т.е
в этой точке будет зависеть от координат точки, т.е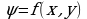 . Перейдем теперь к задаче нахождения массы рассматриваемой фигуры по данной функции
. Перейдем теперь к задаче нахождения массы рассматриваемой фигуры по данной функции 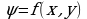 . Разобьем фигуру Д на части
. Разобьем фигуру Д на части 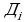 , являющиеся какими-либо квадрируемыми фигурами без общих внутренних точек и имеющими площади
, являющиеся какими-либо квадрируемыми фигурами без общих внутренних точек и имеющими площади 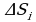 (
(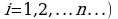 . Выберем в пределах каждой площадки
. Выберем в пределах каждой площадки 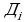 произвольным образом точку
произвольным образом точку 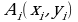 . Будем считать из наглядных соображений, что при малой площади
. Будем считать из наглядных соображений, что при малой площади 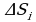 значение плотности
значение плотности 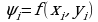 в точке
в точке 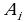 будет мало отличаться от значений плотности в остальных точках этой же части
будет мало отличаться от значений плотности в остальных точках этой же части 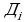 , и мы можем приближенно принять за массу части
, и мы можем приближенно принять за массу части 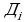 произведение
произведение 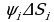 , а сумму таких произведений для всех частей
, а сумму таких произведений для всех частей 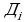 :
:
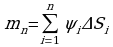 - за приближенное выражение массы всей пластинки. При этом ясно, что чем больше n (тогда размеры каждой части
- за приближенное выражение массы всей пластинки. При этом ясно, что чем больше n (тогда размеры каждой части 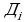 меньше),тем естественнее видеть в сумме
меньше),тем естественнее видеть в сумме 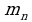 приближенное значение массы пластинки. Поэтому за массу пластинки можно принять предел этой суммы, при условии что
приближенное значение массы пластинки. Поэтому за массу пластинки можно принять предел этой суммы, при условии что 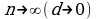 , где d- наибольшее расстояние между точками частичных областей
, где d- наибольшее расстояние между точками частичных областей 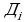 . Таким образом, мы получили
. Таким образом, мы получили
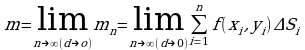
Сравнивая полученную формулу с определением двойного интеграла, получим:
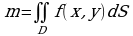
Рассмотрим пример.
Плоское кольцо ограничено двумя концентрическими окружностями 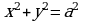 и
и 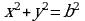
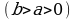 . Зная, что плотность материала кольца в данной точке обратно пропорциональна расстоянию этой точки от общего центра О этих окружностей, найти массу кольца(плотность на окружности внутреннего круга равна
. Зная, что плотность материала кольца в данной точке обратно пропорциональна расстоянию этой точки от общего центра О этих окружностей, найти массу кольца(плотность на окружности внутреннего круга равна 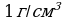 .
.
Решение:
Здесь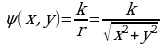 , где к – коэффициент пропорциональности. По условию, при
, где к – коэффициент пропорциональности. По условию, при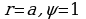 , поэтому к=а и
, поэтому к=а и 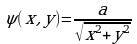 . Находим массу:
. Находим массу:
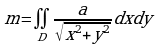 . В полярных координатах уравнения линий, ограничивающих кольцо, будут:
. В полярных координатах уравнения линий, ограничивающих кольцо, будут:  и
и 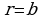 , причем
, причем 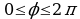 . Поэтому
. Поэтому 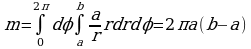
Литература:
Шипачев В.С. Задачник по высшей математике: Учебное пособие для вузов – М. Высшая школа, 2001.- 345с.
Шипачев В.С. Основы высшей математики: Учебное пособие для вузов – М: Высшая школа, 1998.- 380с.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, в 2-х частях Ч.1,Ч.2.:Учебн. пособие для вузов – М.: Высшая школа, 1999.- 280с.







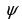 - ее плотность , то вычисление массы производится непосредственно:
- ее плотность , то вычисление массы производится непосредственно: 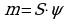 ,где S-площадь фигуры.
,где S-площадь фигуры.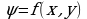 . Перейдем теперь к задаче нахождения массы рассматриваемой фигуры по данной функции
. Перейдем теперь к задаче нахождения массы рассматриваемой фигуры по данной функции 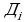 , являющиеся какими-либо квадрируемыми фигурами без общих внутренних точек и имеющими площади
, являющиеся какими-либо квадрируемыми фигурами без общих внутренних точек и имеющими площади 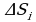 (
(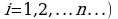 . Выберем в пределах каждой площадки
. Выберем в пределах каждой площадки 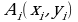 . Будем считать из наглядных соображений, что при малой площади
. Будем считать из наглядных соображений, что при малой площади 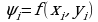 в точке
в точке 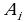 будет мало отличаться от значений плотности в остальных точках этой же части
будет мало отличаться от значений плотности в остальных точках этой же части 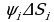 , а сумму таких произведений для всех частей
, а сумму таких произведений для всех частей 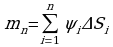 - за приближенное выражение массы всей пластинки. При этом ясно, что чем больше n (тогда размеры каждой части
- за приближенное выражение массы всей пластинки. При этом ясно, что чем больше n (тогда размеры каждой части 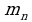 приближенное значение массы пластинки. Поэтому за массу пластинки можно принять предел этой суммы, при условии что
приближенное значение массы пластинки. Поэтому за массу пластинки можно принять предел этой суммы, при условии что 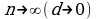 , где d- наибольшее расстояние между точками частичных областей
, где d- наибольшее расстояние между точками частичных областей 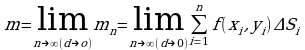
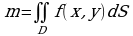
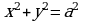 и
и 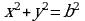
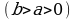 . Зная, что плотность материала кольца в данной точке обратно пропорциональна расстоянию этой точки от общего центра О этих окружностей, найти массу кольца(плотность на окружности внутреннего круга равна
. Зная, что плотность материала кольца в данной точке обратно пропорциональна расстоянию этой точки от общего центра О этих окружностей, найти массу кольца(плотность на окружности внутреннего круга равна 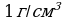 .
.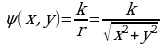 , где к – коэффициент пропорциональности. По условию, при
, где к – коэффициент пропорциональности. По условию, при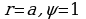 , поэтому к=а и
, поэтому к=а и 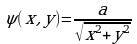 . Находим массу:
. Находим массу: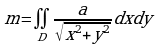 . В полярных координатах уравнения линий, ограничивающих кольцо, будут:
. В полярных координатах уравнения линий, ограничивающих кольцо, будут:  и
и 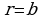 , причем
, причем 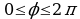 . Поэтому
. Поэтому