Практическое занятие
Вычисление площадей поверхностей и объемов многогранников.
Теоретический этап (Приложение)
Подготовительный этап
Перепишите и заполните пропуски:
Пример 1. Высота правильной треугольной пирамиды 4 см, а ее апофемы 8 см. Вычислите площадь боковой поверхности пирамиды.

Дано: SABC – правильная пирамида, h = SO = 4 см, l = SD = 8 см
Найти: Sбок
Решение: Т.к. пирамида правильная, то Sбок = 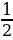 Росн ∙ l
Росн ∙ l
Pосн = 3а, а = 2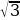 ∙ r, r = OD.
∙ r, r = OD.
Из прямоугольного 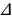 SOD по теореме Пифагора:
SOD по теореме Пифагора:
r = OD = 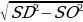 =
= 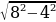 =
= 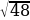 = 4
= 4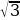 (см)
(см)
Тогда по свойству равностороннего треугольника a = 2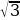 ∙ 4
∙ 4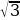 = 24 (см).
= 24 (см).
Теперь, зная размер основания найдем периметр основания: Pосн = 3 ∙ 24 = … (см)
Откуда площадь боковой поверхности пирамиды Sбок = 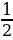 ∙ 72 ∙ 8 = … (см2 )
∙ 72 ∙ 8 = … (см2 )
Ответ: 288 см2.
Пример 2. Дано: правильная усеченная пирамида, n = 4, h = 3, 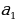 = 16
= 16 ,
, 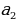 = 8 . Найти: Sполн
= 8 . Найти: Sполн 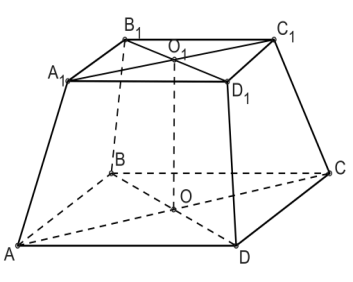
Решение: Sполн = S1осн + S2осн + Sбок
Т.к пирамида правильная, то основания – квадраты.
S1осн = 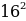 = … , S2осн = 82 = …
= … , S2осн = 82 = …
Sбок = 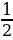 l (P1 + P2 ), P1 = 4 ∙ 16 = … , P2 = 4 ∙ 8 = …,
l (P1 + P2 ), P1 = 4 ∙ 16 = … , P2 = 4 ∙ 8 = …,
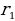 =
= 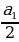 =
= 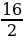 = … ,
= … , 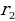 =
= 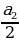 =
= 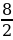 = …,
= …,
l2 = h2 + (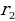 -
- 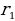 )2, l2 = 32 + (4
)2, l2 = 32 + (4 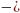 8)2 = 9 + 16 = …, l = ….
8)2 = 9 + 16 = …, l = ….
Sбок = 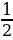 ∙ 5 ∙ (64 + 32) = 5 ∙ 48 = …, Sполн = 256 + 64 + 240 = …
∙ 5 ∙ (64 + 32) = 5 ∙ 48 = …, Sполн = 256 + 64 + 240 = …
Ответ: 560
Пример 3. Площадь грани прямоугольного параллелепипеда равна 12 см2. Ребро, перпендикулярное этой грани, равно 4 см. Найдите объем параллелепипеда.
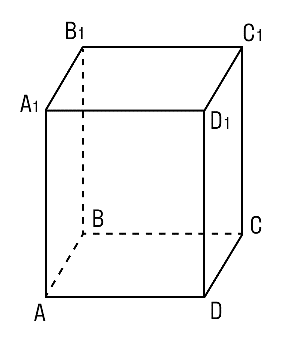
Дано: ABCDA1B1C1D1 прямоугольный параллелепипед, SABCD = 12 см2 , АА1 = 4 см
Найти: V
Решение: V = a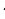 b
b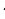 h
h
Каждая грань прямоугольного параллелепипеда – прямоугольник.
SABCD = a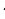 b = 12 см2 , тогда АА1= h = 4 см, т.к. АА1 ⊥ АВСD
b = 12 см2 , тогда АА1= h = 4 см, т.к. АА1 ⊥ АВСD
Используем формулу V = 12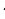 4 = ... (см3)
4 = ... (см3)
Ответ: 48 см3.
Пример 4. Два ребра прямоугольного параллелепипеда (рис. к Примеру 3), выходящие из одной вершины, равны 2 см и 4 см. Диагональ параллелепипеда равна 6 см. Найдите объем параллелепипеда.
Дано: ABCDA1B1C1D1 прямоугольный параллелепипед, a = 4 см, b = 2 см, d = 6 см
Найти: V
Решение:
Формула объема прямоугольного параллелепипеда: V = a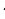 b
b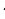 h
h
Формула диагонали прямоугольного параллелепипеда:
d2 = a2 + b2 + h2, 36 = 16 + 4 + h2, h2 = … , h = ... (см), V = 4 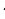 2
2 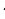 4 = ... (см3 )
4 = ... (см3 )
Ответ: 32 см3.
Пример 5. Стороны основания прямоугольного параллелепипеда 3 см и 4 см (рис. к Примеру 3). Найти его объём, если высота равна длине диагонали его основания.
Дано: ABCDA1B1C1D1 прямоугольный параллелепипед, a = 3 см, b = 4 см, h = BD
Найти: V
Решение: BD - диагональ основания прямоугольного параллелепипеда.
Из прямоугольного треугольника ABD по теореме Пифагора: BD2 = АВ2 + АD2,
BD2 = 32 + 42 = 9 + 16 = …, BD = … см, h = 5 см. V = 3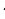 4
4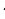 5 = … (см3).
5 = … (см3).
Ответ: 60 см3.
Практический этап
Высота правильной треугольной пирамиды 8 см, а ее апофемы 16 см. Вычислите площадь боковой поверхности пирамиды.
Дано: правильная усеченная пирамида, n = 4, h = 8, 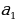 = 16
= 16 ,
, 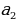 = 4 . Надо найти площадь полной поверхности усеченной пирамиды.
= 4 . Надо найти площадь полной поверхности усеченной пирамиды.
Площадь грани прямоугольного параллелепипеда равна 15 см2. Ребро, перпендикулярное этой грани, равно 6 см. Найдите объем параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 см и 4 см. Диагональ параллелепипеда равна 13 см. Найдите объем параллелепипеда.
Стороны основания прямоугольного параллелепипеда 6 см и 8 см. Найти его объём, если высота равна длине диагонали его основания.
Дополнительные задания*
Дана правильная четырехугольная пирамида со стороной основания a = 12 см и высотой h = 8 см. Найдите площадь полной поверхности пирамиды.
Найдите объем прямоугольного параллелепипеда с ребрами 3 см, 5 см и 8 см.
Длина прямоугольной комнаты в 2 раза больше ширины и на 2 м больше высоты. Найдите объем комнаты, если ее длина равна 6 м.
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1; 0,5; 16. Найдите ребро равновеликого ему куба.








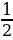 Росн ∙ l
Росн ∙ l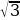 ∙ r, r = OD.
∙ r, r = OD. 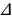 SOD по теореме Пифагора:
SOD по теореме Пифагора: 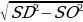 =
= 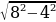 =
= 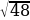 = 4
= 4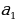 = 16
= 16 ,
, 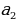 = 8 . Найти: Sполн
= 8 . Найти: Sполн 
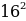 = … , S2осн = 82 = …
= … , S2осн = 82 = …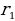 =
= 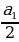 =
= 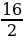 = … ,
= … , 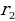 =
= 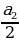 =
= 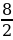 = …,
= …,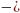 8)2 = 9 + 16 = …, l = ….
8)2 = 9 + 16 = …, l = ….
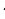 b
b









