Просмотр содержимого документа
«Вычисление статических моментов и координат центра тяжести плоской фигуры»
ББК 22.21
ВЫЧИСЛЕНИЕ СТАТИЧЕСКИХ МОМЕНТОВ И КООРДИНАТ ЦЕНЬРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ
А.С. Тирский, старший преподаватель кафедры
«Естетственных и технических наук»,
К.В. Майоров, студент группы Мех 09
Олёкминский филиал
ФГБОУ ВПО Якутская ГСХА»,, г. Олёкминск
Как известно, математика все больше и больше внедряет свои методы в технические науки. Целью такого внедрения является оптимизация решения данной задачи. Кроме того, зачастую решить задачу можно только математически. Рассмотрим одну из таких задач механики «Вычисление статических моментов и координат центра тяжести плоской материальной фигуры»
Пусть дана материальная плоская фигура(пластинка), ограниченная кривой 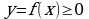 и прямыми
и прямыми 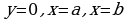 . Будем считать, что поверхностная плотность
. Будем считать, что поверхностная плотность 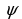 пластинки постоянна . Тогда масса всей пластинки равна
пластинки постоянна . Тогда масса всей пластинки равна 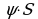 , т.е.
, т.е. 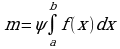 . Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.
. Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.
Тогда масса его равна 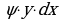 . Центр тяжести С прямоугольника лежит на пересечении диагоналей прямоугольника. Эта тоска С отстоит от оси Ох на
. Центр тяжести С прямоугольника лежит на пересечении диагоналей прямоугольника. Эта тоска С отстоит от оси Ох на 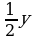 , а от оси Оу на х (приближенно). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения:
, а от оси Оу на х (приближенно). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения:
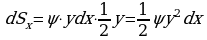 и
и 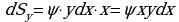 , следовательно, получим
, следовательно, получим
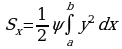 и
и 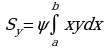 .
.
По аналогии с получением координат центра тяжести С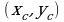 плоской кривой, получаем координаты центра тяжести плоской фигуры(пластинки)
плоской кривой, получаем координаты центра тяжести плоской фигуры(пластинки)
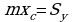 и
и 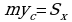 . Отсюда
. Отсюда 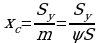 и
и 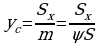 , или
, или
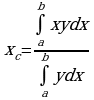
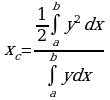
Рассмотрим пример: Найдем координаты центра тяжести полукруга 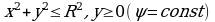
Решение: Очевидно, ввиду симметрии фигуры относительно оси Оу, 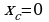 . Площадь полукруга равна
. Площадь полукруга равна 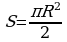 . Находим
. Находим 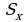 :
:
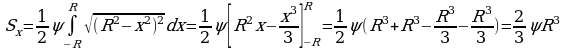 .
.
Таким образом, получаем:
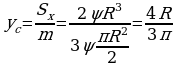 . Итак, центр тяжести имеет координаты:
. Итак, центр тяжести имеет координаты: 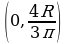 .
.
Литература:
Шипачев В.С. Задачник по высшей математике: Учебное пособие для вузов – М. Высшая школа, 2001.- 345с.
Шипачев В.С. Основы высшей математики: Учебное пособие для вузов – М: Высшая школа, 1998.- 380с.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, в 2-х частях Ч.1,Ч.2.:Учебн. пособие для вузов – М.: Высшая школа, 1999.- 280с.







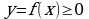 и прямыми
и прямыми 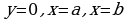 . Будем считать, что поверхностная плотность
. Будем считать, что поверхностная плотность 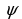 пластинки постоянна . Тогда масса всей пластинки равна
пластинки постоянна . Тогда масса всей пластинки равна 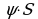 , т.е.
, т.е. 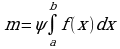 . Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.
. Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.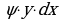 . Центр тяжести С прямоугольника лежит на пересечении диагоналей прямоугольника. Эта тоска С отстоит от оси Ох на
. Центр тяжести С прямоугольника лежит на пересечении диагоналей прямоугольника. Эта тоска С отстоит от оси Ох на 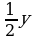 , а от оси Оу на х (приближенно). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения:
, а от оси Оу на х (приближенно). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения: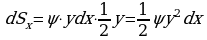 и
и 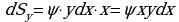 , следовательно, получим
, следовательно, получим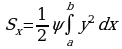 и
и 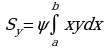 .
. 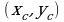 плоской кривой, получаем координаты центра тяжести плоской фигуры(пластинки)
плоской кривой, получаем координаты центра тяжести плоской фигуры(пластинки) 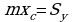 и
и 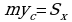 . Отсюда
. Отсюда 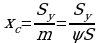 и
и 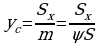 , или
, или 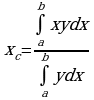
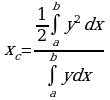
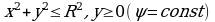
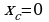 . Площадь полукруга равна
. Площадь полукруга равна 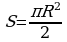 . Находим
. Находим 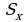 :
: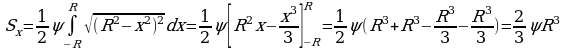 .
.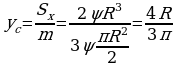 . Итак, центр тяжести имеет координаты:
. Итак, центр тяжести имеет координаты: 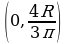 .
.









