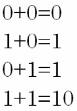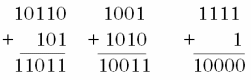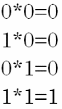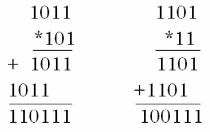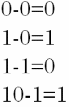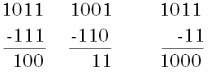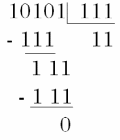Выполнение арифметических операций с дополнительным двоичным кодом целых чисел

Тема: "Выполнение арифметических операций с дополнительным двоичным кодом целых чисел".

Цель работы: 

Получение практических навыков выполнения арифметических операций с дополнительным двоичным кодом целых чисел.

Количество часов на выполнение работы

Продолжительность выполнения данной практической работы составляет 2 академических часа.

Оборудование

• тетрадь;

• ручка (карандаш);

• калькулятор.

Краткие теоретические сведения

Система счисления – совокупность приемов и правил для обозначения и наименования чисел. Системы счисления подразделяются на позиционные (десятичная, двоичная, восьмеричная, шестнадцатеричная) и непозиционные (римская система счисления).

Алфавит системы счисления – множество всех символов (знаков), используемых для записи чисел в данной системе счисления.

Система счисления называется непозиционной, если количественный эквивалент значения любого символа не зависит от его положения (позиции) в коде числа.

Пример: Римская система счисления (2,5тыс. лет до н.э.) 1 -I, 10 - Х, 100 -C, 1000 -M, 5 -V, 50 -L, 500 -D

Для записи числа его раскладывают на сумму цифр 1000, 500, 100, 50, 10, 5, 1.

Система счисления называется позиционной, если количественный эквивалент (значение символа) зависит от его положения в записи числа.

Базисом позиционной системы счисления называется последовательность чисел, каждое из которых определяет количественный эквивалент (вес) символа в зависимости от его места в коде числа.

Основанием позиционной системы счисления называется целое число, которое возводится в степень для получения базиса. Основание в позиционной системе счисления показывает, во сколько раз изменяется вес цифры при перемещении ее на соседнюю позицию. За основание системы счисления можно принять любое натуральное число n (n=1 - недопустимо, т.к. получим унарную систему счисления).

Для того чтобы лучше освоить системы счисления, необходимо освоить выполнение арифметических действий над числами в различных системах счисления.

Все позиционные системы счисления ”одинаковы”, а именно, во всех них арифметические операции выполняются по одним и тем же правилам:

• справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный;

• справедливы правила сложения, вычитания, умножения и деления столбиком;

• правила выполнения арифметических операций опираются на таблицы сложения и умножения.

Правила сложения:

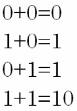
Рисунок 1 – Правила сложения разрядов двоичных чисел

Результат сложения двух единиц: ноль и единица переноса в старший разряд.

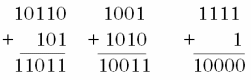
Рисунок 2 – Примеры сложения двоичных чисел

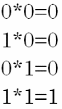
Рисунок 3 – Правила умножения разрядов двоичных чисел

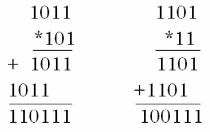
Рисунок 4 – Примеры умножения двоичных чисел

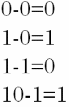
Рисунок 5 – Правила вычитания разрядов двоичных чисел

Из нуля вычесть единицу нельзя, поэтому для вычитания необходимо занять единицу у старшего разряда.

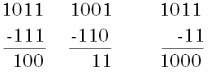
Рисунок 6 – Примеры вычитания двоичных чисел

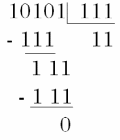
Рисунок 7 – Пример деления двоичных чисел

Задания по практической работе

1. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 110100100₂ и 100011₂.

2. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 100110100₂ и 11100₂.

3. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 101111001₂ и 11101₂.

4. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 110111100₂ и 101100₂.

5. Выполнить в двоичной системе счисления сложение, вычитание, умножение и деление чисел: 101101100₂ и 11010₂.

Контрольные вопросы

1. Что такое система счисления?

2. Какие системы счисления называются непозиционными?

3. Что такое основание, алфавит и базис системы счисления?

4. По каким правилам выполняются арифметические операции с дополнительным двоичным кодом целых чисел?