Муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа №16
Конспект проекта по алгебре
для 9 класса
Автор: Кобелева Ю.А.
учитель математики
Березники.
Урок по алгебре в 9 классе
«Наиболее глубокий след оставляет то, что человек открыл сам». ( Д. Пойя.)
Тема урока: «Вывод формул для вычисления координат вершины параболы».
Цели урока: познавательные:
-
Создать условия для включения учащихся в проблемную ситуацию, принятия и разрешения возникшей проблемы.
-
Формировать учебно - интеллектуальные умения: анализировать, обобщать, сравнивать.
-
Формировать умения применять ранее полученные знания о функции 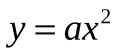 для получения новых знаний.
для получения новых знаний.
-
Нахождение нового способа определения координат вершины и оси симметрии параболы квадратичной функции 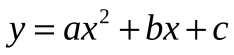 .
.
Метапредметные, в том числе: регулятивные: поставить учебную задачу на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно; определить последовательность действий для решения поставленной задачи; откорректировать результат с учётом оценки самим обучающимся, учителем, учениками; осознать качество и уровень усвоения нового материала. Коммуникативные: научиться инициативному сотрудничеству в поиске решения поставленной задачи; научиться с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.
Ожидаемый результат:
- осознание, принятие и разрешение проблемы учащимися;
-формирование способов получения новых знаний через сравнение и сопоставления фактов, способа от частного к общему;
- узнают формулы нахождения координат вершины и оси симметрии параболы для функций вида 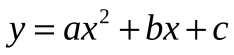
Тип урока: урок постановки учебной задачи.
Методы обучения – наглядно-иллюстративный, словесный, обучение в сотрудничестве, проблемный, элементы технологии критического мышления.
Оборудование: компьютер, мультимедийный проектор, демонстрационный экран, слайды презентации по теме: «Формулы для нахождения координат вершины параболы»; листы формата А3; цветные маркеры.
Технология - системно-деятельностный подход.
Этапы урока:
-
Психологический настрой(мотивация).
-
Актуализация опорных знаний(создание ситуации успеха).
-
Постановка проблемы.
-
Формулирование темы и цели урока.
-
Решение проблемы.
-
Анализ хода решения проблемы.
-
Применение результатов решения проблемы в последующей деятельности.
-
Подведение итогов урока (итог «глазами» ученика, итог «глазами» учителя.).
-
Домашнее задание.
Ход урока:
1) Психологический настрой.
Задача: Учится решать общую задачу и работать в коллективе (работа в группах по 5 чел.).
Ребята, на протяжении последних четырёх уроков мы занимались изучением квадратичной функции, но знания наши пока ещё не совсем полные, поэтому мы продолжаем изучать квадратичную функцию с целью узнать что-то новое об этой функции.
Мотивация учащихся к самостоятельной постановке темы и цели урока.
| Тема урока …. |
|
|
| Знаю 1. 2. 3. …….. | Хочу знать 1. 2. 3. …….. | Узнал 1. 2. 3. …….. |
Таблица заполняется по ходу проведения урока.
2) Актуализация опорных знаний и умений учащихся.
Разминка. 1. Вынести за скобки старший коэффициент: 5x2 + 25x -5; ax2 + bx + c.
2. Выделить удвоенное произведение: ab; ax; b/a.
3. Возвести в квадрат: b/2; c2/a; 2a/3b.
4. Представить в виде алгебраической суммы: а – в; x –(- b/2a).
Объясните, как, зная вид графика функции y =ƒ(x), построить графики функций:
а) y =ƒ(x - a), - с помощью параллельного переноса на а единиц вправо вдоль оси х;
б) y =ƒ(x) + b, - с помощью параллельного переноса на b единиц вверх вдоль оси y;
в) y =ƒ(x - а) + b, ↔ на а единиц, ↕ на b единиц;
г) Как построить график функции y = (x - 2) 2 + 3 ? Что является ее графиком?
Назовите вершину параболы.
Графиком является парабола y = x2 с вершиной в точке (2; 3).
Назовите координаты вершины параболы: y =x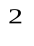 - 4x + 5 (проблема). Почему нельзя определить координаты вершины параболы по виду функции? (другой вид имеет квадратичная функция).
- 4x + 5 (проблема). Почему нельзя определить координаты вершины параболы по виду функции? (другой вид имеет квадратичная функция).
Деятельность учащихся:
Строят речевые конструкции с использованием функциональной терминологии.
Обсуждение ответов. Сравнивают, сопоставляют с ранее изученными функциями, выбирают и записывают на доске знания и умения, которые им могут понадобиться для решения проблемы в столбик «ЗНАЮ»:
1.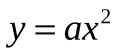
2. 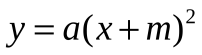
3. 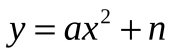
4. 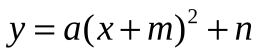
5. знаю, как построить графики этих функций
6. знаю, как найти координаты вершины этих парабол и ось параболы
В столбик «Хочу узнать»: вершину, ось симметрии параболы 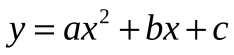 .
.
Учащиеся могут записывать в столбики «ЗНАЮ» и «ХОЧУ ЗНАТЬ» функции как в общем виде, так и частные случаи. Постановка учебной задачи: найти координаты вершины параболы, если квадратичная функция задана в общем виде  y = ax
y = ax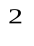 + bx + c. Учащиеся формулируют и записывают в тетрадь тему и цель урока. (Вывод формул для вычисления координат вершины параболы. Научиться находить координаты вершины параболы новым способом – по формулам).
+ bx + c. Учащиеся формулируют и записывают в тетрадь тему и цель урока. (Вывод формул для вычисления координат вершины параболы. Научиться находить координаты вершины параболы новым способом – по формулам).
4. Решение проблемы.
Деятельность учащихся: Сравнивая «старые» знания с новыми знаниями учащиеся предлагают выделить полный квадрат. На конкретных примерах 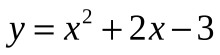 ;
; 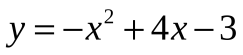 и получают соответственно
и получают соответственно 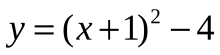 ;
; 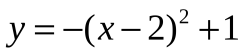 . Находят координаты вершины и уравнение оси симметрии, Понимают, что с задачей справились, т.к. привели новую функцию к знакомому виду.
. Находят координаты вершины и уравнение оси симметрии, Понимают, что с задачей справились, т.к. привели новую функцию к знакомому виду.
Учащиеся выделяют полный квадрат для функции 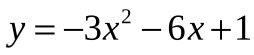 ;
; 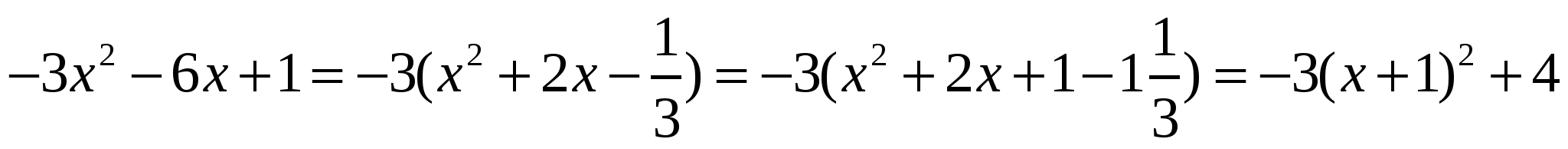 , сравнивают полученный результат, делают вывод по данной функции. Находят координаты вершины и ось симметрии.
, сравнивают полученный результат, делают вывод по данной функции. Находят координаты вершины и ось симметрии.
Сможете ли вы назвать вершину и ось параболы, если функция задана в общем виде 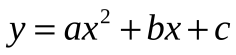 , не выделяя полного квадрата? Как вы будете действовать в этом случае? И как применить ваш предыдущий опыт по нахождению вершины и оси параболы?
, не выделяя полного квадрата? Как вы будете действовать в этом случае? И как применить ваш предыдущий опыт по нахождению вершины и оси параболы?
Деятельность учащихся:
Опираясь на уже имеющиеся знания, опыт учащиеся начинают понимать, что нужно идти дальше, от частного к общему, проводят доказательства в общем виде.
. Появляются новые затруднения. В группах появляется решение:
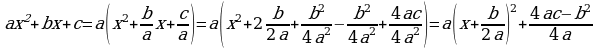 .
.
-
Анализ хода решения проблемы.
-
Формулировка и запись способа решения.
Заслушивается один представитель от каждой группы.
Сравнивают, анализируют записи 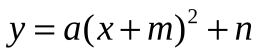 и
и 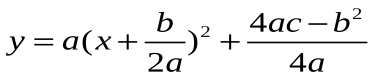 , записывается в тетрадь одно общее решение поставленной задачи - формулы координат вершины параболы
, записывается в тетрадь одно общее решение поставленной задачи - формулы координат вершины параболы 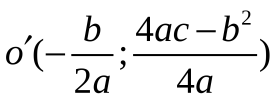 .
.
Учащиеся делают вывод: координаты вершины и ось параболы для функции 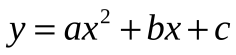 можно найти рациональным способом.
можно найти рациональным способом.
7. Применение результатов по решению проблемы в последующей деятельности.
Деятельность учащихся:
Решение заданий из учебника №121 (Функция 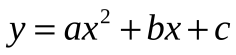 и ее график.)
и ее график.)
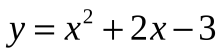 ;
; 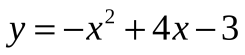 ;
; 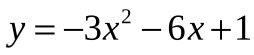
Не выполняя построения графика функций, можем ли мы ответить на вопросы:
-
Что является графиком функций?
-
Какая прямая является осью симметрии (если она существует)?
-
Есть ли вершина, каковы её координаты? Назовите координаты вершины параболы новым рациональным способом.
Запишите уравнение прямой, которая является осью симметрии параболы.
8. Подведение итогов (рефлексия учебной деятельности на уроке).
Вернемся к таблице и заполним столбик «УЗНАЛ».
Итог урока «глазами» учащихся:
| ЗНАЮ | ХОЧУ ЗНАТЬ | УЗНАЛ |
| 1.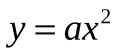 2. 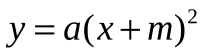 3. 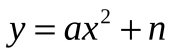 4. 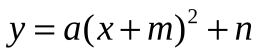 5. знаю, как построить графики этих функций 6. знаю, как найти координаты вершины этих парабол и ось параболы 7. метод выделения полного квадрата 8. как находить координаты вершин, ось параболы. | 1. координаты вершины параболы 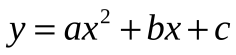
2. уравнение оси симметрии параболы 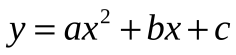
| 1. координаты вершины параболы 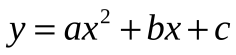 2 .как вывести формулу 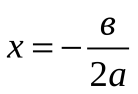 3. рациональный способ нахождения оси параболы и координат вершины параболы
|
Итог « глазами учителя»:
-
Цель урока достигнута.
-
Учащиеся осознали, приняли и разрешили возникшую проблему.
-
В процессе решения учебно-проблемной задачи учащиеся не только приобрели новые знания: зависимость коэффициентов квадратного трехчлена и координат вершины параболы, уравнения оси симметрии, но самое главное на уроке – формирование обобщенных способов приобретения новых знаний, самостоятельного анализа проблемы и нахождения неизвестного.
Домашнее задание: п.7 №122
| Этап урока | Формирование УУД | Деятельность учителя на уроке | Деятельность ученика на уроке |
| Психологический настрой | Формирование мотивации, готовности к саморазвитию, совместному виду деятельности. | Вступительное слово учителя, выдача карточек, анализ содержания карточки | Настраивается на работу, получает карточку, анализирует содержание карточки. |
| Актуализация знаний | Умение анализировать и обобщать изученные знания, достаточно полно и точно выражать свои мысли, развитие самопроверки. | Предлагает знания из уже известного и усвоенного учащимися материала, заполнить карточку. | Решают задания, заполняют первую колонку карточки «ЗНАЮ». |
| Постановка проблемы, цели | Умение поставить и сформулировать учебную задачу (развитие грамотной математической речи), цель занятия, планирование их реализации (определение последовательности поставленной задачи). | Постановка проблемного задания. Записывает тему на доске. | Обсуждение задания, осознание проблемы. Заполняют второй столбик карточки «ХОЧУ ЗНАТЬ». Формулируют проблему, ставят учебную задачу (в карточке), записывают тему урока в тетради |
| Решение проблемы | Развитие навыков учебного сотрудничества в поисках решения поставленной задачи, навыков достижения цели, формирование способов получения новых знаний через сравнение и сопоставление фактов изученного материала. | Регулирует работу групп, оказывает помощь. | Решают поставленную задачу. |
| Анализ и защита решений | Умение внимательно выслушать мнение других, анализировать, сравнивать, оценивать. | Определяет порядок выступлений. | Анализируют результат деятельности группы, защита у доски. Приходят к выводу, что нужен новый способ. Ищут решение в общем виде. |
| Формулировка и запись способа решения | Умение делать выводы, строить алгоритм решения. | Регулирует работу групп, оказывает помощь. | Формулируют новую формулу и алгоритм решения, записывают в тетрадь. |
| Применение способа в последующей деятельности | Применение теоретических положений полученных знаний (воспроизведение на базовом уровне). | Оказывает индивидуальные консультации. | Решают № 121 из учебника. |
| Подведение итогов | Самоанализ и самооценка своей деятельности, полученных результатов, осознание качества и уровня усвоения материала. | Ведет фронтальный опрос, задает домашнее задание. | Анализируют применение нового способа, заполняют колонку «УЗНАЛ», оценивают результат своей деятельности. |






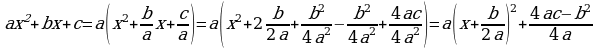 .
. 


















