Зачет по теме «Теорема Пифагора». 8 класс
Цель: - проверить знания, умения и навыки применения теоремы Пифагора при решении
задач;
- развивать логическое мышление, умение анализировать и сравнивать, развивать
вычислительные навыки; умения построения чертежей в измененных условиях;
- воспитывать самостоятельность, внимательность и аккуратность в учебной
работе;
Практическая часть включает в себя 4 варианта дифференцированных задач. 1 и 2 варианты равнозначны по сложности предлагаемых заданий и соответствуют обязательному уровню усвоения материала; 3 вариант и 4 вариант зачетной работы представляют более сложные задания, требующих дополнительных знаний и более высокого уровня вычислительной культуры.
На выполнение работы отводиться 40 минут.
Ответы к заданиям зачетной работы
|
| Задача 1
| Задача 2 | Задача 3 | Задача 4 | Задача 5 |
| Вариант 1 | c =10 см (1б)
| b = 5 см (1б) | h =15 см (1б) | P = 62 cм (1б) | S = 96 см2 (1б) |
| Вариант 2 | c =13 см (1б)
| b = 24 см (1б) | h =8 см (1б) | P = 34 cм (1б) | S = 54 см2 (1б) |
| Вариант 3 | c =17 см (1б)
| P = 52 cм (1б) | PΔ = 52 cм (2б) 36 | абок = 20см (1б) | абок =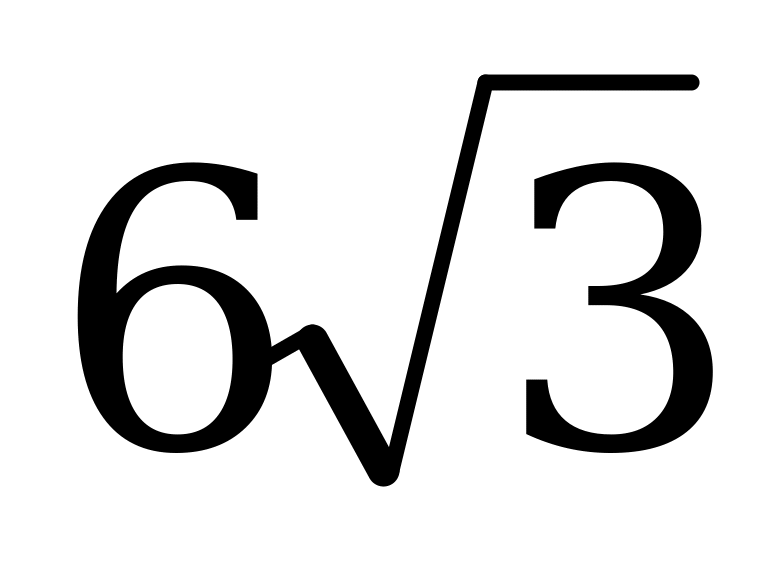 см (2б) см (2б) |
| Вариант 4 | c =25 см (1б) | b = 45 см (1б) c =53 см | Sтрап= 36 см2 (2б) | абок = 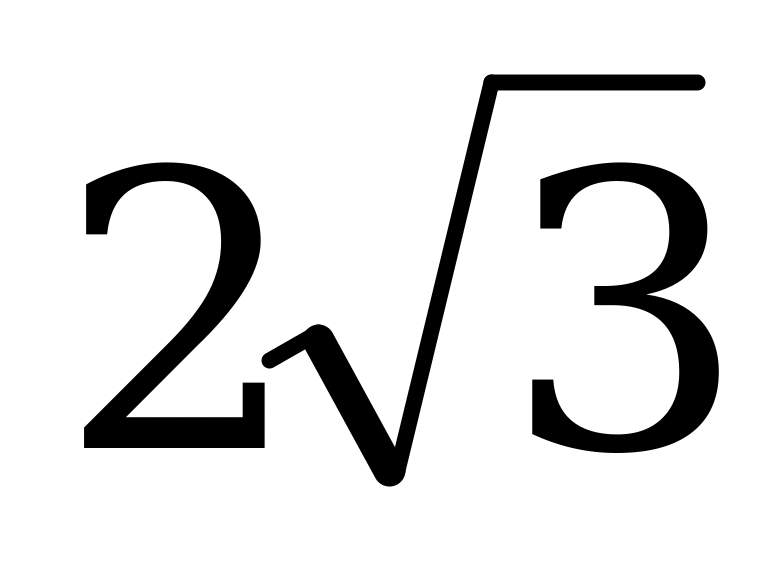 см см (1б) | D = 20 cм (1б) |
 Критерии оценивания зачетной работы
Критерии оценивания зачетной работы
За каждое правильно решенное задание дается 1 балл в 1 и 2 вариантах, в 3 и 4 вариантах
по 1 баллу за задачи № 1, 2 и № 4, по 2 балла - за задачи № 3, 5.
| 1 вариант 2 вариант | Количество баллов | 0- 2 балла | 3 - 4 балла | 5 баллов |
-
|
| Оценка | «2» | «3» | «4» |
| 3 вариант 4 вариант | Количество баллов | 0- 2 балла | 3 - 4 балла | 5 - 6 баллов | 7 баллов |
| Оценка | «2» | «3» | «4» | «5»
|
Вариант – 1
1. В прямоугольном треугольнике катеты равны 8 см и 6 см. Найдите гипотенузу этого треугольника.
2. Гипотенуза прямоугольного треугольника равна 13 см, а катет равен 12 см. Найдите другой катет.
3. Боковая сторона равнобедренного треугольника равна 17 см, его основание равно 16 см. Найдите высоту, проведенную к основанию.
4. Одна сторона прямоугольника равна 7 см, а диагональ равна 25 см. Найдите периметр прямоугольника.
5. Катеты прямоугольного треугольника относятся как 3: 4, гипотенуза равна 20 см. Найдите площадь этого треугольника.
Вариант – 2
1. В прямоугольном треугольнике катеты равны 12 см и 5 см. Найдите гипотенузу этого треугольника.
2. В прямоугольном треугольнике один из катетов равен 7 см, гипотенуза равна 25 см. Найдите второй катет.
3. В равнобедренном треугольнике боковая сторона равна 10 см, его основание равно 12 см. Найдите высоту, проведенную к основанию треугольника.
4. Диагональ прямоугольника равна 13 см, одна из его сторон равна 5 см. Найдите периметр прямоугольника.
5. Катет прямоугольного треугольника равен 9 см, а гипотенуза и второй катет относятся как
5 : 4. Найдите площадь этого треугольника.
Вариант – 3
1. В прямоугольном треугольнике катеты равны 15 см и 8 см. Найдите гипотенузу треугольника.
2. Диагонали ромба равны 10 см и 24 см. Найдите периметр ромба.
3. Катет прямоугольного треугольника равен 9 см, а гипотенуза больше второго катета на 3 см. Найдите периметр треугольника.
4. В равнобедренном треугольнике основание равно 24 см, высота, проведенная к основанию, равна 16 см. Найдите боковую сторону треугольника.
5. Найдите сторону равностороннего треугольника, если его высота равна 9 см.
Вариант – 4
1. В прямоугольном треугольнике катеты равны 7см и 24 см. Найдите гипотенузу треугольника.
2. Катет прямоугольного треугольника равен 28 см. Разность двух других сторон равна 8 см. Найдите неизвестные стороны этого треугольника.
3. В равнобедренной трапеции основания равны 6 см и 12 см., боковая сторона равна 5 см. Найдите площадь трапеции.
4. Высота равностороннего треугольника равна 3 см. Найдите сторону этого равностороннего треугольника.
5. Расстояние от хорды к центру окружности 6 см, длина хорды 16 см. Найдите диаметр этой окружности.















