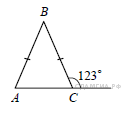| Билет 1 Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств. Признаки равенства прямоугольных треугольников
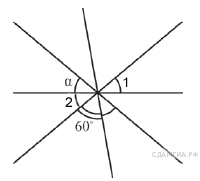
Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.
|
| Билет 2 1. Параллелограмм. Признаки параллелограмма. Доказательство одного из признаков 2. Прямоугольный треугольник. Свойства прямоугольного треугольника. 3. Задание 9 № 311514. На плоскости даны четыре прямые. Известно, что 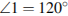 , , 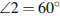 , , 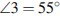 . Найдите . Найдите  . Ответ дайте в градусах. . Ответ дайте в градусах. 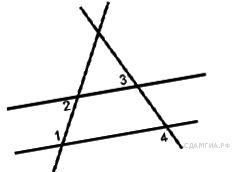
|
| Билет 3 Теорема о соотношениях между сторонами и углами треугольника. Неравенство треугольника Прямоугольник. Свойства прямоугольника. Доказательство особого свойства прямоугольника.
Задание 9 № 340052. На прямой AB взята точка M. Луч MD — биссектриса углаCMB. Известно, что ∠DMC = 60°. Найдите угол CMA. Ответ дайте в градусах. 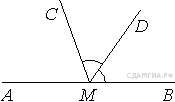
|
| Билет 4 Прямоугольник. Признак прямоугольника. Доказательство признака прямоугольника. Внешний угол треугольника.Виды треугольников Биссектриса угла А параллелограмма АВСD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 15 см, КС = 9 см.
|
| Билет 5 Ромб. Свойства ромба. Доказательство одного из свойств. Теорема о сумме углов треугольника.Доказательство. Найдите площадь треугольника, изображённого на рисунке. ![]()   20 12 13 ![]() ![]()
 
5 11
|
| Билет 6 Аксиома параллельных прямых. Следствия. Квадрат. Свойства квадрата. Доказательство одного из свойств. Найдите площадь ромба, если его диагонали равны 4 м и 6 м.
|
| Билет 7 Теорема Пифагора. Доказательство. Признаки параллельности прямых. Задание 12 № 311400. На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах. 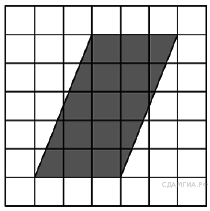
|
| Билет 8 Определение параллельных прямых. Углы, образованные при пересечение двух прямых секущей. Теоремы об отношении площадей треугольников. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма. 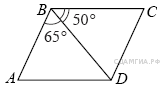
|
| Билет 9 Формула площади ромба (через диагонали; задача 476). Вывод Сформулируйте и докажите свойство биссектрисы равнобедренного треугольника, проведённой к его основанию. На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.

|
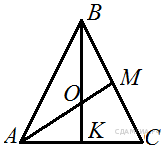
| Билет 10 Сформулируйте свойства смежных и вертикальных углов и докажите одно из них на ваш выбор. Формула площади параллелограмма В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите 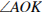 . .
 |
| Билет 11 Формула площади треугольника. Сформулируйте свойство углов при основании равнобедренного треугольника и
докажите его. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
|
| Билет 12 Первый, второй и третий признаки равенства треугольников. Формула площади трапеции. Вывод. Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол. Ответ дайте в градусах.
|
| Билет 13 Сумма углов выпуклого многоугольника. Вывод. Смежные и вертикальные углы. Определение и чертёж. Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах. |
| Билет 14 Равнобедренный треугольник, его элементы. Равносторонний треугольник.
Свойства равнобедренного треугольника. Определение подобных треугольников. Отношение площадей подобных треугольников Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
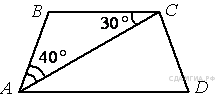
|
| Билет 15 Признаки подобия треугольников Треугольник. Медиана, биссектриса и высота треугольника и их
свойства Задание 9 № 339377. Прямые m и n параллельны. Найдите ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в градусах. 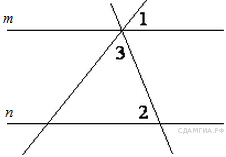 |
| Билет 16 Перпендикулярные прямые, их обозначение. Перпендикуляр к прямой, основание
перпендикуляра. Признаки подобия треугольников На прямой AB взята точка M. Луч MD — биссектриса углаCMB. Известно, что ∠DMC = 60°. Найдите угол CMA. Ответ дайте в градусах. 
|
| Билет 17 Средняя линия треугольника. Доказательство теоремы Отрезок. Середина отрезка. Луч. Угол. Биссектриса угла. Виды углов (прямой, острый,
тупой, развёрнутый) Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? 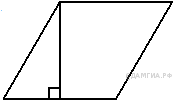
|
| Билет 18 Пропорциональные отрезки в прямоугольном треугольнике. Определение параллельных прямых. Углы образованные при пересечение двух прямых секущей
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине Cравен 123°. Найдите величину угла ABC. Ответ дайте в градусах. 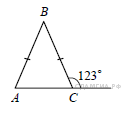
|