Зачет по материалам ФИПИ задания типа В9

Зачет по В9

1)Объем куба равен 8. Найдите площадь его поверхности.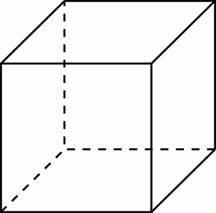

№2 Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .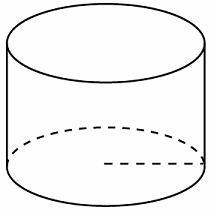

№3 Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

№4 Прямоугольный параллелепипед описан около сферы радиуса . Найдите его объем.

Зачет по В9

№1 Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.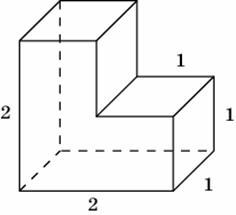

№2 Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 16.

№3 Объем конуса равен 120. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

№4 Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.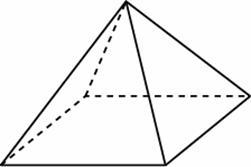

Зачет по В9

Найдите обьем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

№2 Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14.

№3 В основании прямой призмы лежит квадрат со стороной 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.

№4 №4 Прямоугольный параллелепипед описан около сферы радиуса . Найдите его объем.

Зачет по В9

№1Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.

№2 Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 18.

№3 Объем конуса равен 168. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

№4 Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.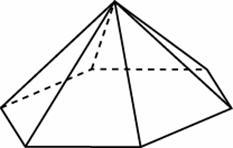

Зачет по В9

Найдите обьем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

№2 Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 11.

№3 Объем конуса равен 64. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

№4 В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого?

Зачет по В9

№1Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?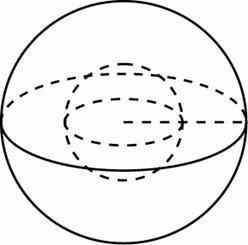

№2Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

№3 Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра

№4 В основании прямой призмы лежит квадрат со стороной 4. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.

Зачет по В9

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

№2 Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.

№3 Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

№4 Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.

Зачет по В9

№1 Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

№2 Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза

№3 Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .

№4 В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

Зачет по В9

№1 В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого?

№2 Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

№3 Объем параллелепипеда равен . Найдите объем треугольной пирамиды .

№4 В основании прямой призмы лежит квадрат со стороной 6. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.

Зачет по В9

№1 Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

№2 Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.

№3 Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.

№4 В основании прямой призмы лежит прямоугольный треугольник с катетами 9 и 6. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.

Зачет по В9 Харченко

№1 Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите

№2 Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

№3 Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.

№4 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4. Площадь ее поверхности равна 132. Найдите высоту призмы.

Зачет по В9 Фроленко

№1 Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите

№2 Найдите объем V части конуса, изображенной на рисунке. В ответе укажите

№3 В основании прямой призмы лежит квадрат со стороной 5. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.

№4 Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 63.

Зачет по В9

№1 Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

№2 Объем конуса равен 24. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

№3 Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

№4 Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на

Зачет по В9

№1 Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

№2 Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .

№3 Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите

№4 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.