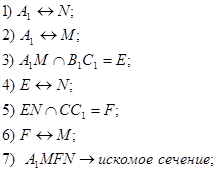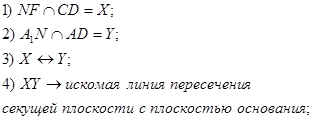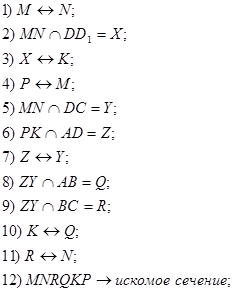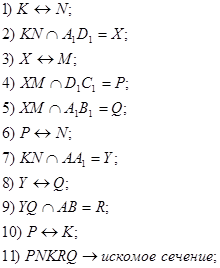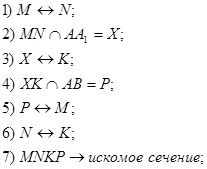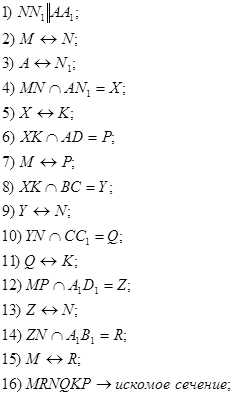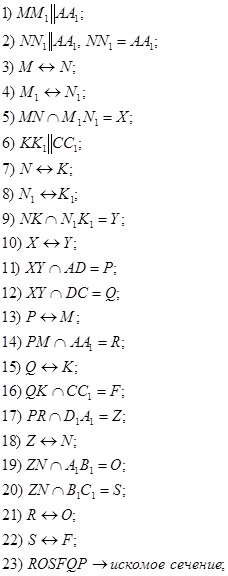Просмотр содержимого документа
«Задачи для работы в классе для учащихся 10 класса по теме "Построение сечений"»
| Построить сечения многогранников плоскостью, проходящей через три выделенные точки. |
| 1 | 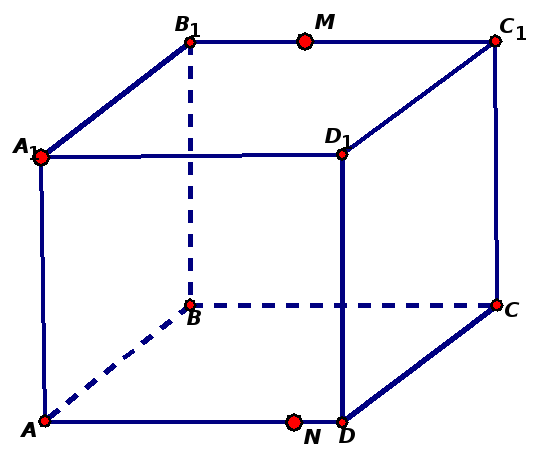
| 6 | 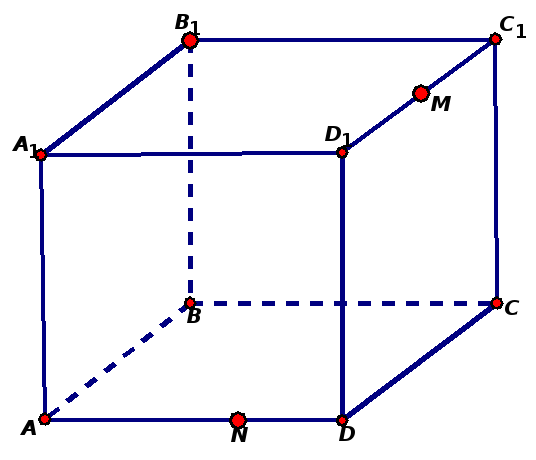
|
| 2 | 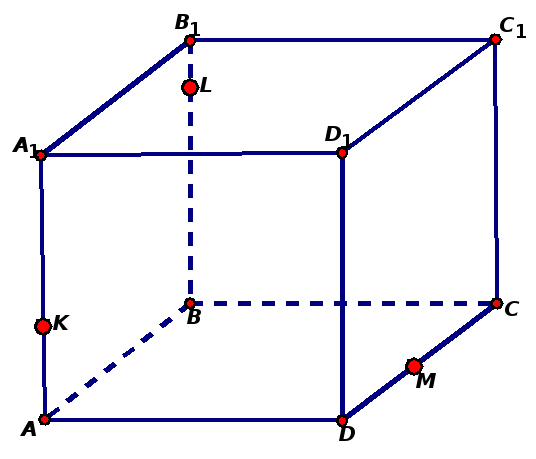
| 7 | 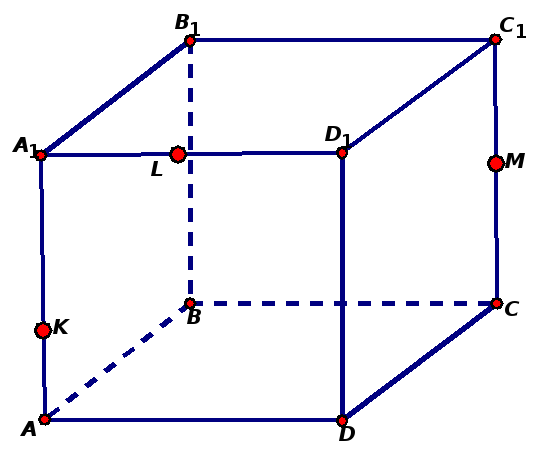
|
| 3 | 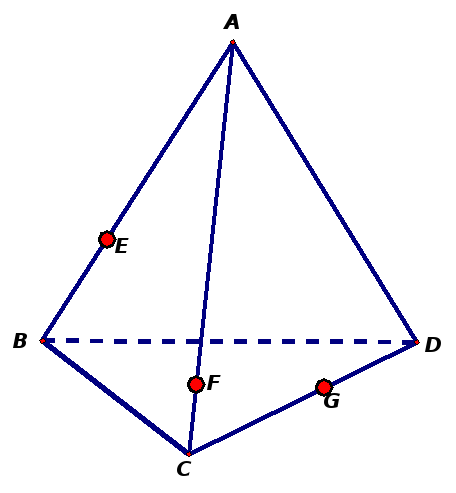
| 8 | 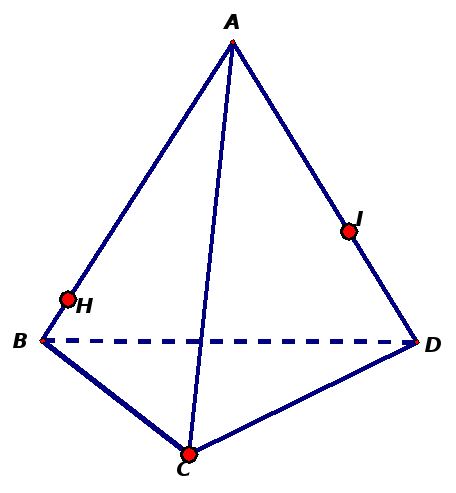
|
| 4 | 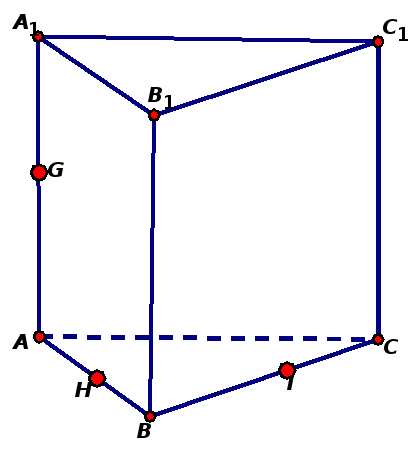
| 9 | 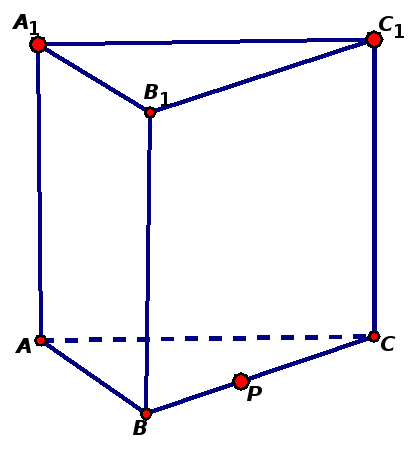
|
| 5 | 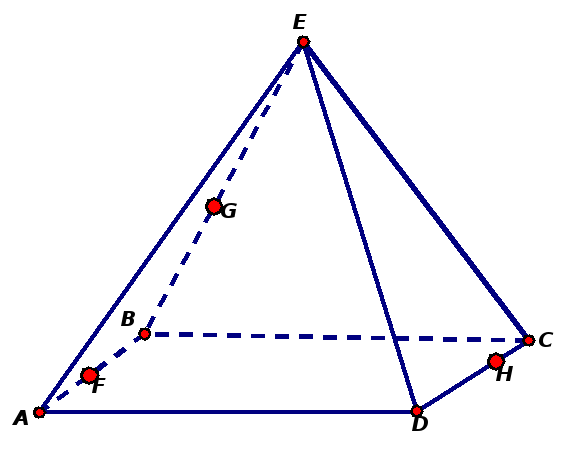
| 10 | 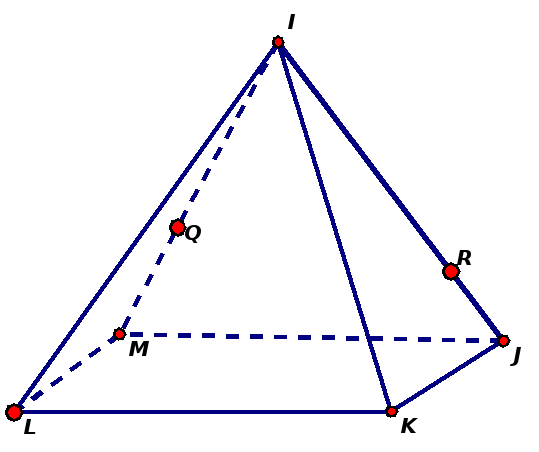
|
Задачи на построение сечений.
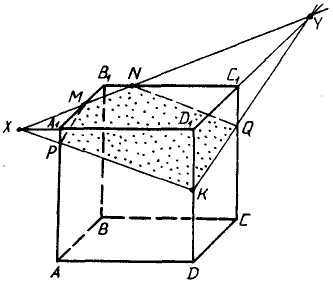
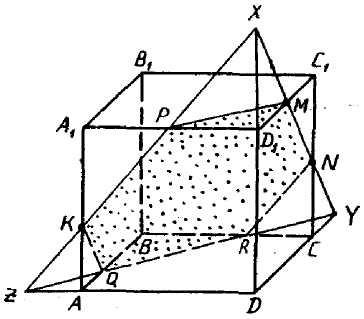
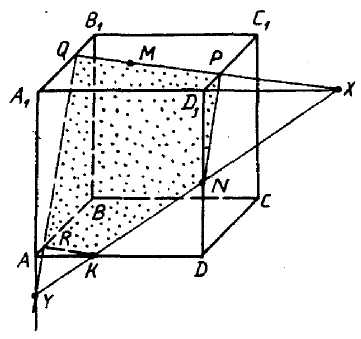
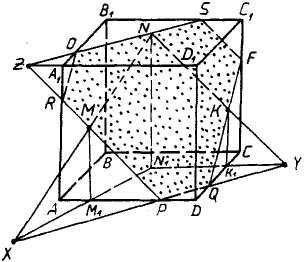
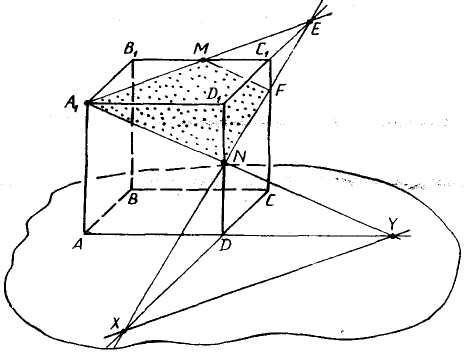
Задача 1. Построить сечение куба плоскостью, проходящей через точки A1, M ∈ B1C1 и N ∈ DD1 и найти линию пересечения секущей плоскости с плоскостью нижнего основания куба.
Задача 2. Построить сечение куба плоскостью, проходящей через точки: M ∈ A1B1; N ∈ B1C1 и K ∈ DD1.
Задача 3. Построить сечение куба плоскостью, проходящей через точки M ∈ D1C1, N ∈ CC1 и K ∈ AA1.
Задача 4. Построить сечение куба плоскостью, проходящей через точки: M ∈ грани A1B1C1D1; N ∈ DD1 и K ∈ AD.
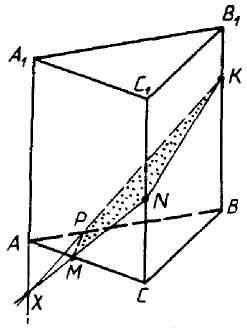
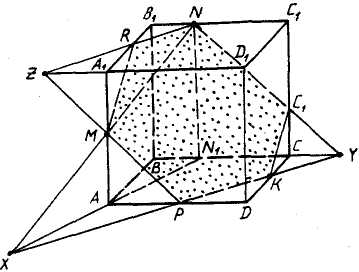
3aдача 5. Построить сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через точки: M ∈ AC; N ∈ CC1; K ∈ BB1 .
Задача 6. Построить сечение куба плоскостью, проходящей через точки: M ∈ AA1; N ∈ B1C1; K ∈ DC. (Точки М, N и К лежат на скрещивающихся ребрах).
Задача 7. Построить сечение куба плоскостью, проходящей через точки: M ∈ AA1D1D; N ∈ A1B1C1D1; K ∈ DDC1C.
Задача 8. В треугольной пирамиде SАВС провести сечение:
а) через середину ребра АС параллельно грани SСВ;
б) через середину ребра SС параллельно грани SАВ.
Задача 9. Дан куб ABCDA1B1C1D1. Постройте сечение куба плоскостью, которая проходит через данные точки: а) С1, К, D; б) С1, К, С, где точка К – середина А1В1. Определите, какая фигура образуется в сечении.
Задача 10. Точка Х делит ребро АВ куба ABCDA1B1C1D1 в отношении АХ : ХВ = 2 : 3. Постройте сечение этого куба плоскостью, которая параллельна плоскости АА1С1 и проходит через точку X. Найдите периметр сечения, если АВ = а.
Задача 5. Построить сечение куба плоскостью, проходящей через точки A1, M ∈ B1C1 и N ∈ DD1 и найти линию пересечения секущей плоскости с плоскостью нижнего основания куба.
| 1-я часть решения 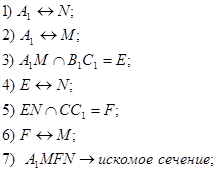
2-я часть решения 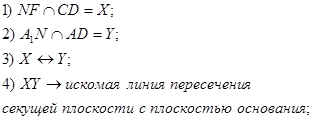
| 
|
Задача 6. Построить сечение куба плоскостью, проходящей через точки: M ∈ A1B1; N ∈ B1C1 и K ∈ DD1.
Задача 7. Построить сечение куба плоскостью, проходящей через точки M ∈ D1C1, N ∈ CC1 и K ∈ AA1.
Задача 8. Построить сечение куба плоскостью, проходящей через точки: M ∈ грани A1B1C1D1; N ∈ DD1 и K ∈ AD.
Зaдача 9. Построить сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через точки: M ∈ AC; N ∈ CC1; K ∈ BB1.
Задача 10. Построить сечение куба плоскостью, проходящей через точки: M ∈ AA1; N ∈ B1C1; K ∈ DC. (Точки М, N и К лежат на скрещивающихся ребрах).
Задача 11. Построить сечение куба плоскостью, проходящей через точки: M ∈ AA1D1D; N ∈ A1B1C1D1; K ∈ DDC1C.
Задача 12. В треугольной пирамиде SАВС провести сечение:
а) через середину ребра АС параллельно грани SСВ;
б) через середину ребра SС параллельно грани SАВ.
Задача 13. Ответ:
а) равнобедренная трапеция; б) прямоугольник.
Задача 14. Ответ:

| Построить сечения многогранника плоскостью, проходящей через три выделенные точки |
|
| |
| |
|
| |
|
|
|
|
|
|
|