Задачи на клетчатой бумаге (Разбор задания №19 из ОГЭ)

Решение задач на нахождение площади геометрических фигур на сетке.

ОГЭ . Задание № 19

Подготовила учитель математики МОУ Школа с.Харсаим Филиппова Р.Р.

Характеристика задания

Задание 19 ОГЭ по математике представляет собой задачу по планиметрии на вычисление по готовому чертежу, изображённому на клетчатой бумаге. В таких задачах данные представлены в виде чертежа на бумаге в клетку, причём размеры клеток одинаковы и заданы условием. Это задачи на вычисление углов, расстояний, площадей, связанные со всеми изучаемыми в школьном курсе фигурами. Клетки в таких задачах по сути выполняют роль линейки: посчитав «по клеточкам» необходимые длины и используя известные геометрические факты и свойства, можно довольно быстро получить ответ на вопрос задачи.

Определение

• Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник

Единицы измерения площади

За единицу измерения площадей принимают квадрат со стороной 1см.

• Квадратный метр , производная единица  Международной системы единиц (СИ) ; 1  м²  = 1 са ( сантиар );
• Квадратный километр , 1 км² = 1 000 000 м²;
• Гектар, 1 га = 10 000 м²;
• Ар (сотка), 1 а = 100 м²:
• Квадратный дециметр, 100 дм² = 1 м²;
• Квадратный сантиметр, 10 000 см² = 1 м²;
• Квадратный миллиметр, 1 000 000 мм² = 1 м²;

Свойства площади

• Фигуры имеющие равные площади называются равновеликими.
• Равные многоугольники имеют равные площади.
• Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
• Площадь квадрата равна квадрату его стороны.

Основные формулы для нахождения площади.

Площади треугольников

S = ½*a*h S = ½*a*b sinα S = r*p

S =

S = - формула Герона

(p = - полупериметр)

S = π*R 2 площадь круга

Основные формулы для нахождения площади.

Площади четырехугольников

Прямоугольник

S=a*b S= ½* d 2 sinφ

а и в – стороны прямоугольника

d - диагональ прямоугольника

φ- угол между диагоналями

Квадрат

S = a 2 S =1/2* d 2

а – сторона квадрата

d - диагональ квадрата

Параллелограмм

S=a*h S=a*b*sinα

S= ½* d 1 *d 2 sinφ

Ромб

S=a*h S=a 2 sinα

S= ½* d 1 *d 2

Трапеция

S = S = ½* d 1 * d 2 sinφ

а и в – основания трапеции; -длина средней линии ; d 1 и d 2 -диагонали трапеции; sinφ -угол между диагоналями

Одним из основных заданий Модуля Геометрия являются задачи на нахождение площади фигур на сетке. Многие ученики сводят решение этого задания к подсчету клеток внутри фигуры. Такой способ не всегда дает точный результат. Поэтому я предлагаю рассмотреть основные способы решения таких задач.

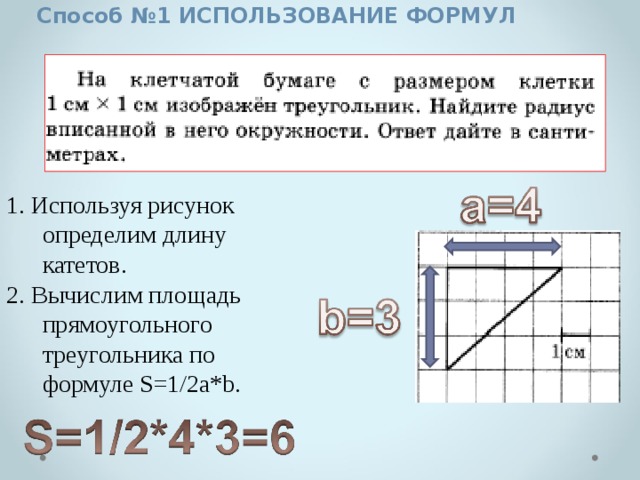
Способ №1 ИСПОЛЬЗОВАНИЕ ФОРМУЛ

1. Используя рисунок определим длину катетов.

2. Вычислим площадь прямоугольного треугольника по формуле S=1/2a*b.

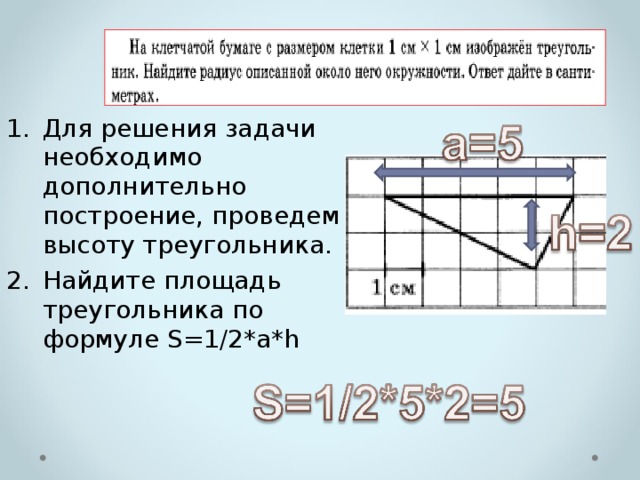
• Для решения задачи необходимо дополнительно построение, проведем высоту треугольника.
• Найдите площадь треугольника по формуле S=1/2*а*h

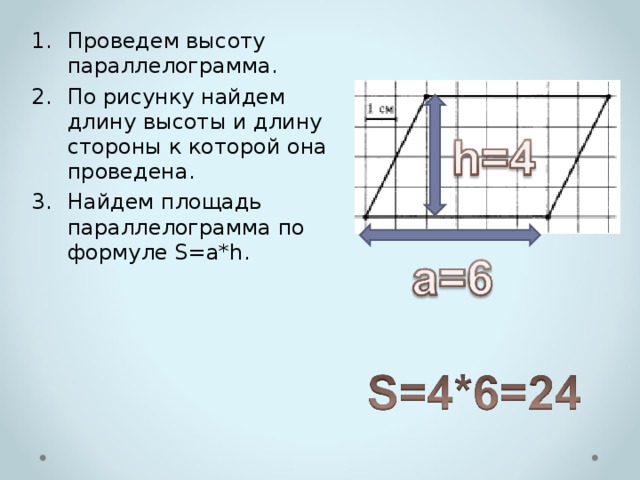
• Проведем высоту параллелограмма.
• По рисунку найдем длину высоты и длину стороны к которой она проведена.
• Найдем площадь параллелограмма по формуле S=a*h.

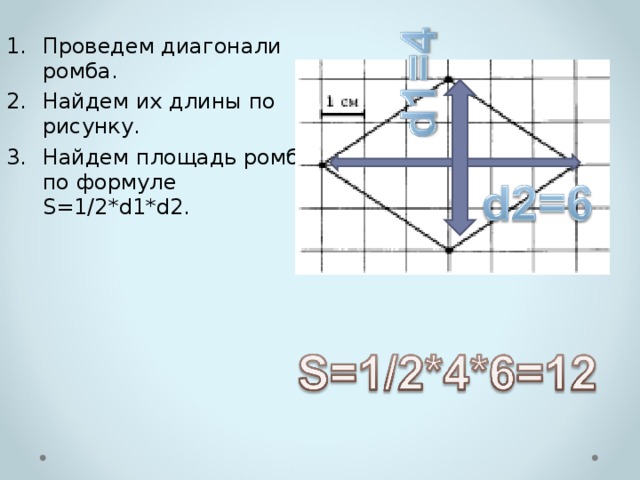
• Проведем диагонали ромба.
• Найдем их длины по рисунку.
• Найдем площадь ромба по формуле S=1/2*d1*d2.

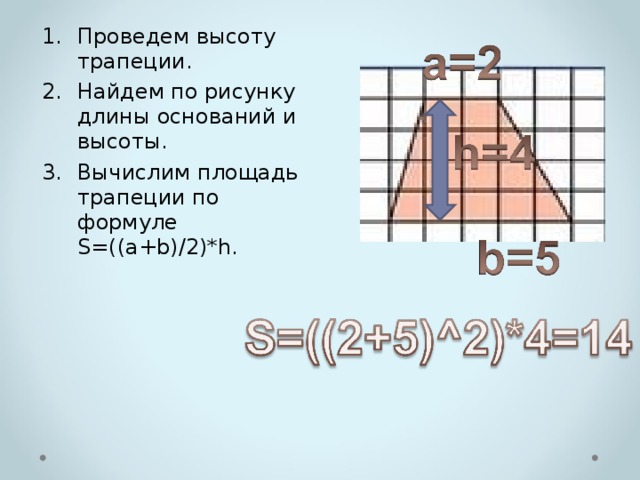
• Проведем высоту трапеции.
• Найдем по рисунку длины оснований и высоты.
• Вычислим площадь трапеции по формуле S=((a+b)/2)*h.

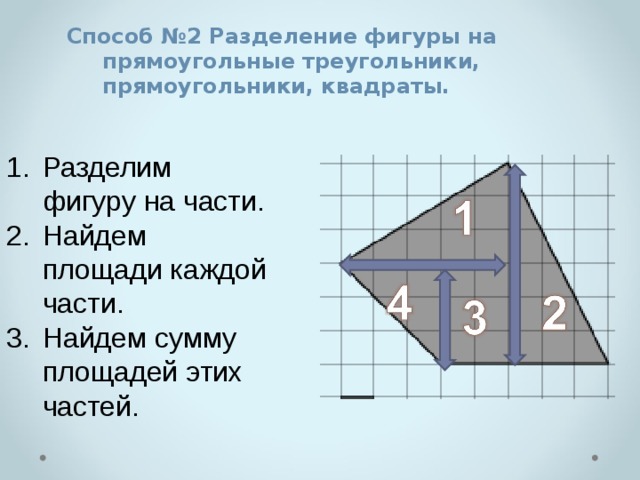
Способ №2 Разделение фигуры на прямоугольные треугольники, прямоугольники, квадраты.

• Разделим фигуру на части.
• Найдем площади каждой части.
• Найдем сумму площадей этих частей.

• Фигуры 1,4,2 –прямоугольные треугольники. Их площади найдем по формуле S=1/2*a*b.
• Фигура 3-прямоугольник. Его площадь легко найти даже подсчетам клеток. Его площадь равна 6.
• Сложив площади треугольников и прямоугольника мы найдем площадь искомой фигуры.

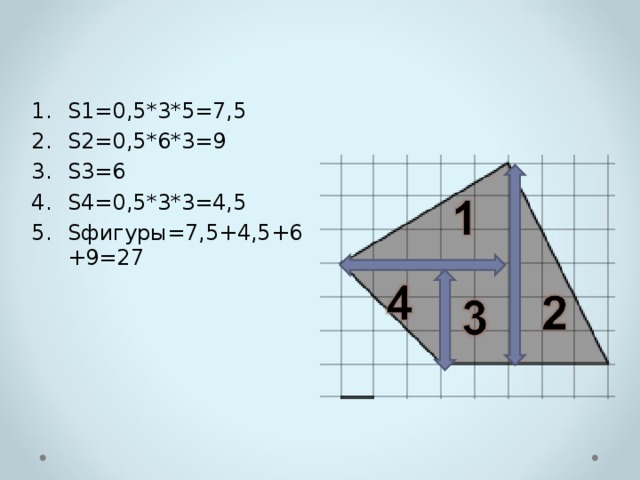
• S1=0,5*3*5=7,5
• S2=0,5*6*3=9
• S3=6
• S4=0,5*3*3=4,5
• Sфигуры=7,5+4,5+6+9=27

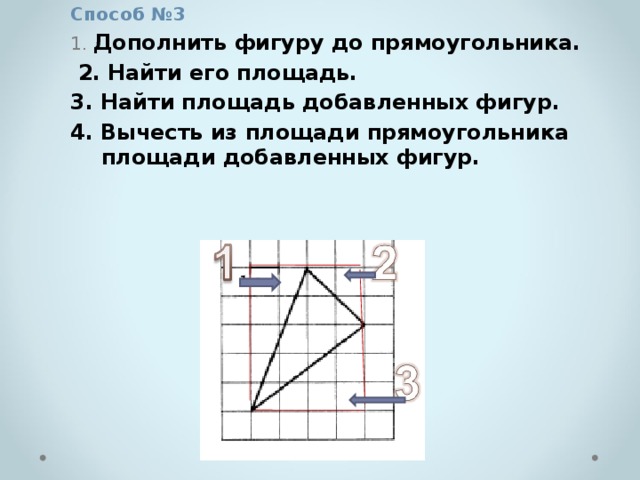
Способ №3

1. Дополнить фигуру до прямоугольника.

2. Найти его площадь.

3. Найти площадь добавленных фигур.

4. Вычесть из площади прямоугольника площади добавленных фигур.

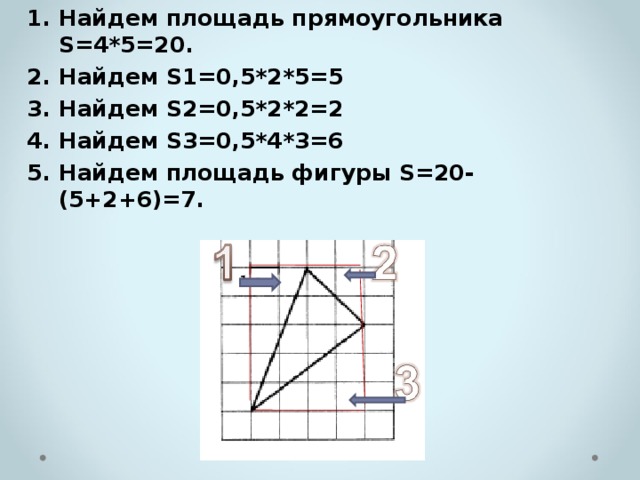
• Найдем площадь прямоугольника S=4*5=20.
• Найдем S1=0,5*2*5=5
• Найдем S2=0,5*2*2=2
• Найдем S3=0,5*4*3=6
• Найдем площадь фигуры S=20-(5+2+6)=7.

Способ №4 Формула Пика.

Площадь многоугольника с целочисленными вершинами равна  В + Г/2 − 1 , где  В  - есть количество целочисленных точек внутри многоугольника, а Г  — количество целочисленных точек на границе многоугольника.

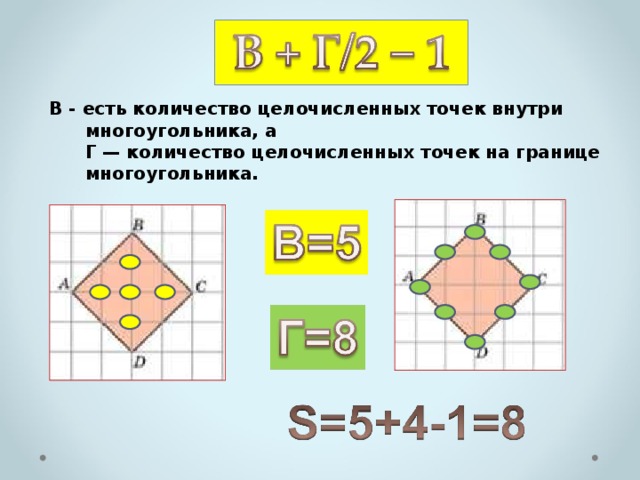
В - есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.

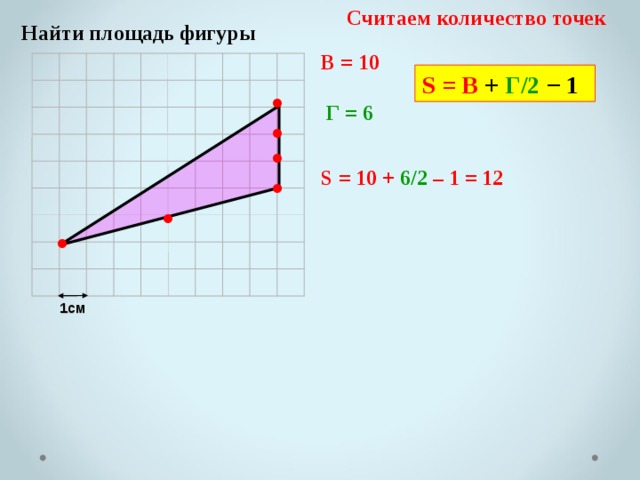
Считаем количество точек

Найти площадь фигуры

В = 10

S = В + Г/2 − 1

●

Г = 6

●

●

S = 10 + 6/2 – 1 = 12

●

●

●

1см

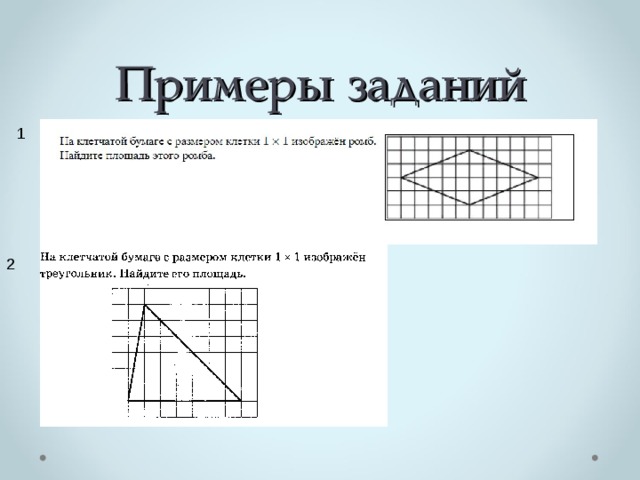
Примеры заданий

1

2

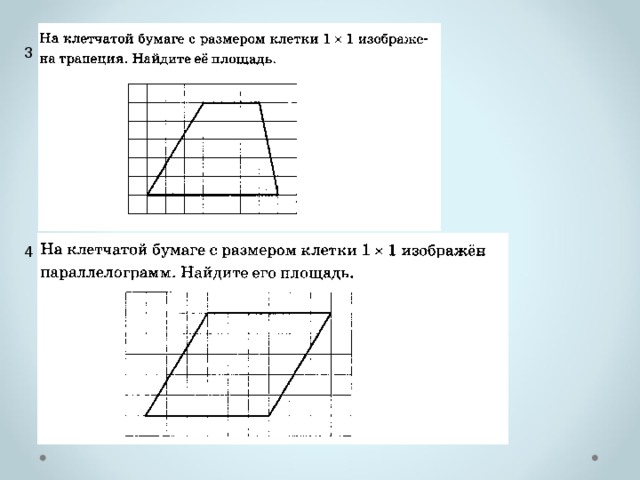
3

4

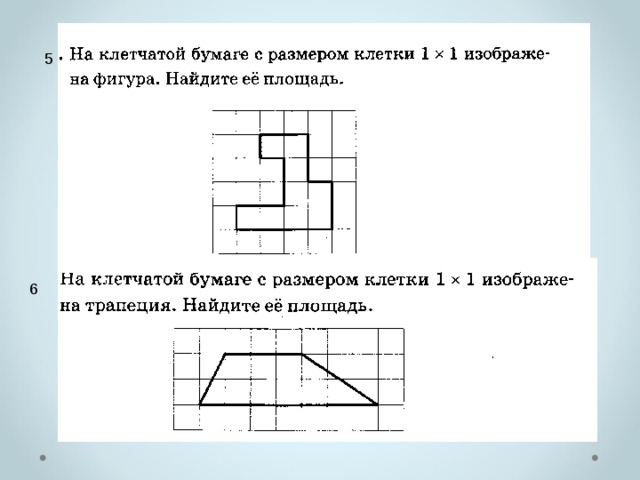
5

6