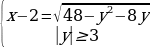Задачи по математическому моделированию 8 класс

Задача 1.

В плоскости лежит треугольник ABC. Угол С острый.

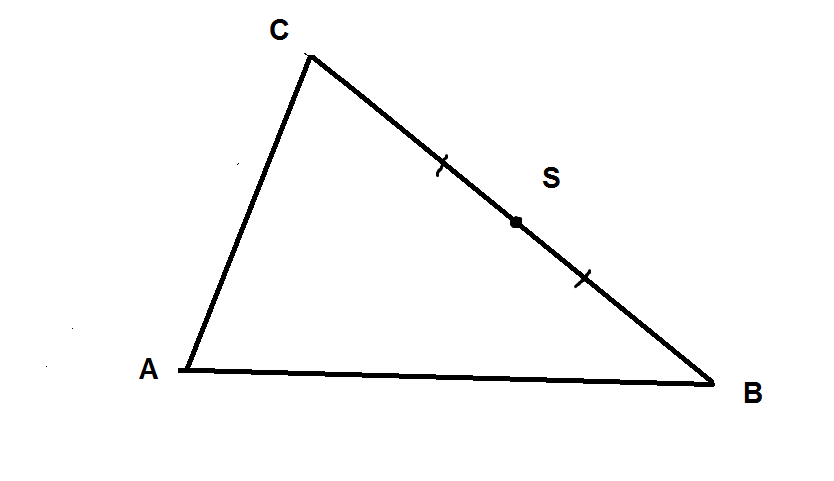
Вершина S квадрата STUV лежит в середине стороны BC, другие вершины не принадлежат стороне BC. Две из трех оставшихся вершин T; U; V квадрата лежат внутри треугольника ABC. Постройте все возможные варианты расположения квадрата STUV на плоскости (возможно выполнить на одном чертеже схематически).

Задача 2.

Запишите все возможные аналитические модели совокупности множества точек, заданных на координатной плоскости

Задача 3.

Составьте модели для решения задачи (решать составленные модели не нужно).

Два поезда выехали одновременно в одном направлении из городов A и B, расположенных на расстоянии 120 км друг от друга, и одновременно прибыли на станцию C. Если бы один из них уменьшил свою скорость на 12 км/ч, а другой на 9 км/ч, то они также прибыли на станцию С одновременно, но на 2 часа позже. Найдите скорости поездов. (Считаем, что пункт В расположен между пунктами А и С).

Задача 4.

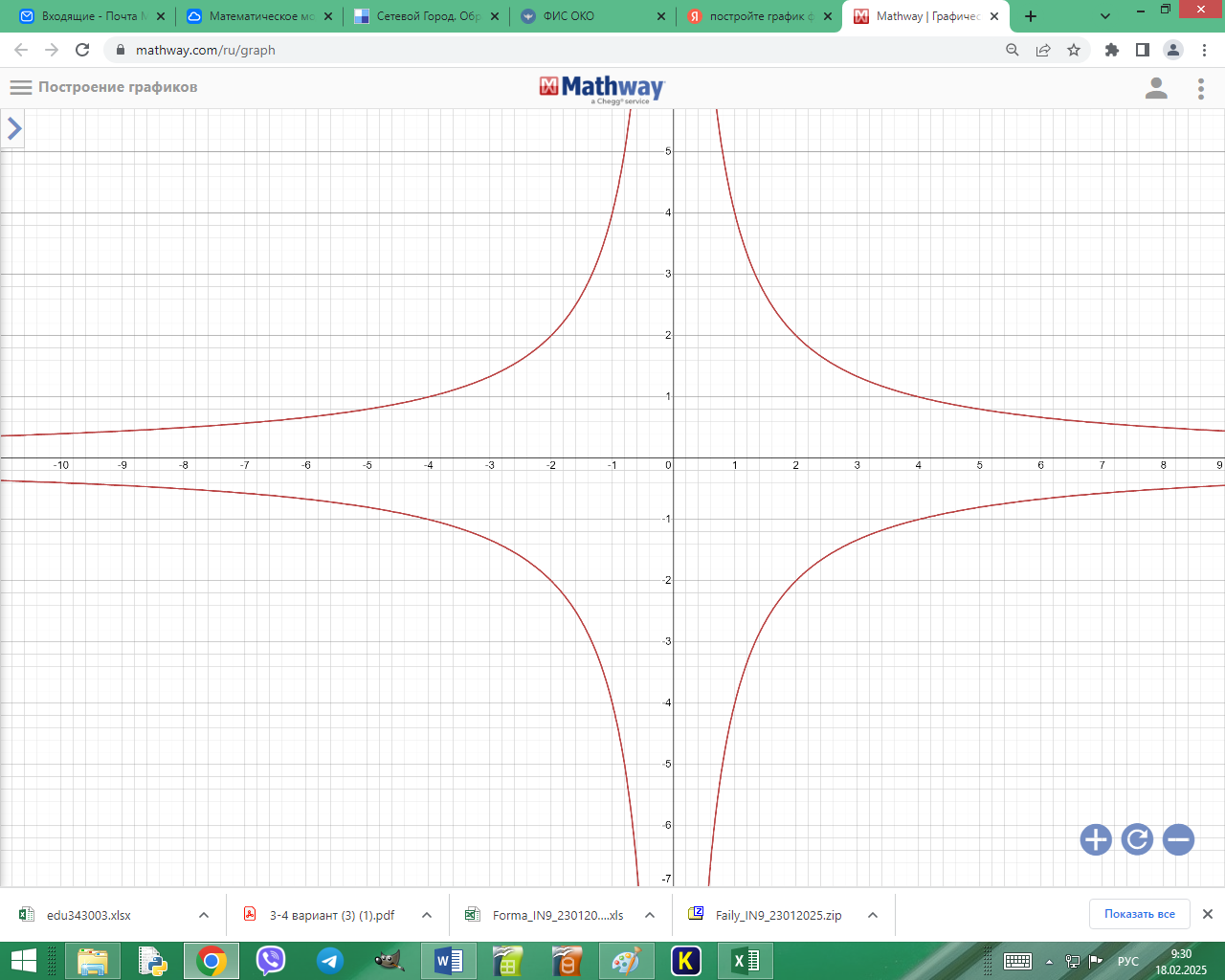
Постройте графическую модель множества точек координатной плоскости, соответствующую условию

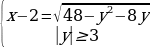
Задача 5.

Сделайте чертеж для решения задачи. Саму задачу решать не нужно.

Окружности радиусов 2 и 10 с центрами О₁ и О₂ соответственно касаются в точке А. Прямая, проходящая через точку А, вторично пересекает меньшую окружность в точке В, а большую - в точке С.

Найдите площадь треугольника BCO₂, если угол ABO₁ равен 22,5°.

Задача 6.

Изобразите все возможные различные графы, с тремя вершинами.