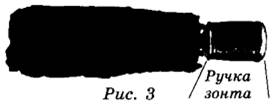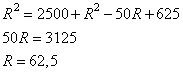Задание 1-5 вариант 3 из 36 вариантов ОГЭ 2023

Задание 1-5 вариант 3 из 36 вариантов ОГЭ 2023

Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

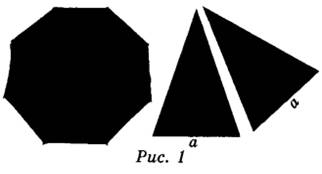
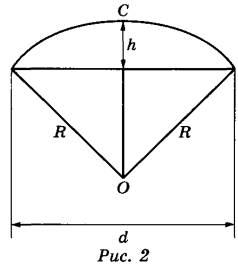
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.

Задание 1. Длина зонта в сложенном виде равна 20 см и складывается из длины ручки (рис. 3) и четверти длины спицы (зонт в четыре сложения). Найдите длину спицы, если длина ручки зонта равна 5,9 см.

Решение.

Четверть спицы будет равна:

20 – 5,9 = 14,1 см

следовательно, длина всей спицы:

14,1 ∙ 4 = 56,4 см

Ответ: 56,4

Задание 2. «Поскольку зонт сшит из треугольников, — рассуждал Петя, — площадь его поверхности можно найти как сумму площадей треугольников». Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение.

Высота h = 53,1 см, проведенная к основанию a = 38 см, дает площадь каждого сегмента, равную:

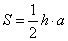
Так как таких сегментов 8, то получаем полную площадь поверхности:

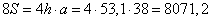 кв. см

Округляем до десятков, получаем 8070 кв. см.

Ответ: 8070

Задание 3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

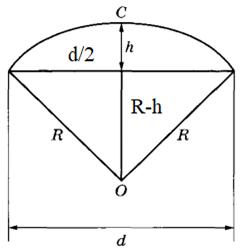
По теореме Пифагора можно записать равенство:

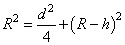
Решаем уравнение относительно R, имеем:

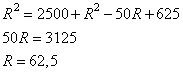
Ответ: 62,5

Задание 4. Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле 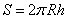 , где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число я округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

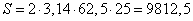
Округляем до целого, имеем: 9813 см. кв.

Ответ: 9813

Задание 5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 35∙100∙80 = 280 000 см. кв.

Площадь клиньев для 29 зонтов, равна:

29∙8∙1050 = 243 600 см. кв.

Площадь обрезков:

280 000 – 243 600 = 36 400 см. кв.

Что составляет:

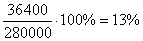
Ответ: 13