ЗАДАНИЕ №12
ИЗ ЕГЭ ПО ПРОФИЛЬНОЙ МАТЕМАТИКЕ
И МЕТОДИКА ЕГО РЕШЕНИЯ
Автор разработки:
Попов Дмитрий Сергеевич
г. Горловка, 2024 г.
Предисловие
Исследование функции – это задача, заключающаяся в определении основных параметров заданной функции. Вообще, это информация, помогающая узнать больше о функции, представить примерно (а затем, может быть, и точно) её график.
Задание №12 из ЕГЭ по профильной математике заключается в исследовании функций с помощью производной функции.
Задачи из задания №12 бывают двух типов:
нахождение точек максимума/минимума, то есть точек, в
которых функция принимает локально самое большое/маленькое
значение;
нахождение наибольшего/наименьшего значения функции
на промежутке.
Чтобы найти наибольшее и наименьшее значения непрерывной на отрезке [a; b] функции, достаточно вычислить значение этой функции в концевых точках, а также во всех точках интервала (a; b), в которых производная равна нулю или не существует, и из полученного набора значений выбрать наибольшее и наименьшее.
Но иногда на этой позиции встречаются задания, которые можно решить без использования производной. Для их решения достаточно уметь исследовать квадратичную функцию.
ВАРИАНТЫ ЗАДАНИЙ И МЕТОДИКА ИХ РЕШЕНИЯ
ТИП №1. Найдите наименьшее значение функции у = 2x – ln(х + 4)2 на отрезке [-3,5; 0].
М Е Т О Д И К А Р Е Ш Е Н И Я.
Для начала в заданиях такого типа необходимо проверить концы данного отрезка. Но здесь, за счёт натурального логарифма никаких целочисленных значений мы не получим, поэтому данный шаг можно опустить.
Нахожу производную функции, но перед этим выношу степень за логарифм:
у = 2x – 2ln(х + 4)
у΄ = 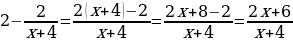 .
.
Приравниваем значение производной функции к нулю:
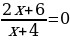
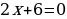
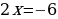
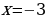
Считаю значение в полученной точке: 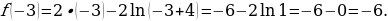
Ответ: 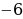 .
.
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите наименьшее значение функции у = 6x – ln(х + 6)6 на отрезке [-5,5; 0].
2) Найдите наименьшее значение функции у = 10x – ln(х + 14)10 на отрезке [-13,5; 0].
3) Найдите наименьшее значение функции у = 12x – ln(х + 20)12 на отрезке [-19,5; 0].
4) Найдите наименьшее значение функции у = 11x – ln(х + 4)11 на отрезке [-3,5; 0].
ТИП №2. Найдите точку максимума функции у = (x – 3)2 е х – 7 .
М Е Т О Д И К А Р Е Ш Е Н И Я.
Нахожу производную функции:
у = (x – 3)2 е х – 7
у΄ = 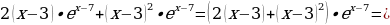
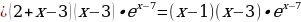
Приравниваем значение производной функции к нулю:
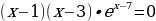
x1 = 1 x2 = 3
Отмечаю точки на чертеже и определяю знаки промежутков:
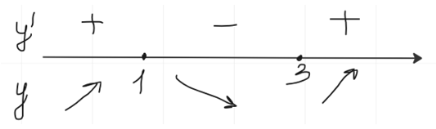
Точка максимума равна 1.
Ответ: 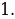
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите точку максимума функции у = (x – 6)2 е х – 3 .
2) Найдите точку максимума функции у = (x + 14)2 е х – 31 .
3) Найдите точку максимума функции у = (x – 10)2 е х – 8.
4) Найдите точку максимума функции у = (x + 16)2 е х – 10.
ТИП №3. Найдите наименьшее значение функции у = x2 – 3х + lnх + 10 на отрезке 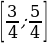 .
.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Проверка концов отрезков не проводится, так как логарифм, который находится в уравнении, является натуральным.
Нахожу производную функции:
у = x2 – 3х + lnх + 10
у΄ = 2х – 3 + 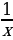
Приравниваю значение производной функции к нулю:
2х – 3 + 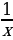 = 0
= 0
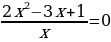
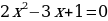
D = 9 – 4 ∙ 2 ∙ 1 = 9 – 8 = 1; 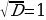 .
.
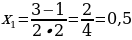 – не принадлежит заданному промежутку
– не принадлежит заданному промежутку 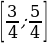 , т.к. 0,5
, т.к. 0,5 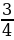 .
.
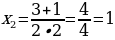 .
.
Вычисляю значение в полученной точке:
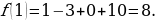
Ответ: 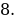
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите наименьшее значение функции у = 2x2 – 5х + lnх – 3 на отрезке 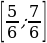 .
.
2) Найдите наименьшее значение функции у = 2x2 – 6х + 2lnх + 7 на отрезке 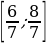 .
.
ТИП №4. Найдите точку минимума функции у = x3 – 3,5х2 + 2х + 16.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Нахожу производную функции:
у = x3 – 3,5х2 + 2х + 16
у΄ = 3х2 – 7х + 2
Приравниваю значение производной функции к нулю:
3х2 – 7х + 2 = 0
D = 49 – 4 ∙ 3 ∙ 2 = 49 – 24 = 25; 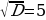 .
.
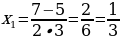
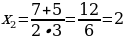 .
.
Отмечаю точки на чертеже и определяю знаки промежутков:
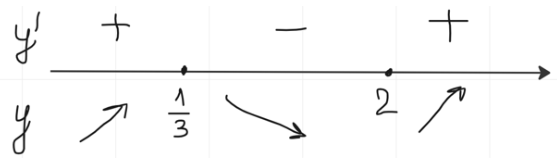
Точка максимума равна 2.
Ответ: 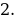
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите точку минимума функции у = x3 + 9,5х2 + 30х + 22.
2) Найдите точку минимума функции у = x3 – 16х2 + 64х + 17.
ТИП №5. Найдите наименьшее значение функции у = 13х – 10 sinx + 1 на отрезке 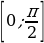 .
.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Считаю значения на концах отрезка. Рациональное значение существует только в точке 0:
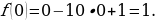
Нахожу производную функции:
у΄ = 13 – 10 cosх
Приравниваю значение производной функции к нулю и решаю уравнение: 13 – 10 cosх = 0
10 cosх = 13
cosх = 1,3 – уравнение решений не имеет т.к. cosx 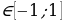 .
.
Ответ выбираем из первого пункта решения.
Ответ: 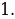
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите наименьшее значение функции у = 7х – 6 sinx + 12 на отрезке 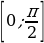 .
.
2) Найдите наименьшее значение функции у = 2х – 2 sinx + 7 на отрезке 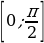 .
.
3) Найдите наименьшее значение функции у = 13х – 5 sinx – 14 на отрезке 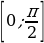 .
.
4) Найдите наименьшее значение функции у = 19х – 10 sinx + 6 на отрезке 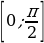 .
.
ТИП №6. Найдите точку минимума функции у = (1 – 2х)cosx + 2sinx + 7, принадлежащую промежутку 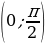 .
.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Нахожу производную функции:
у΄ = – 2cosх + (1 – 2х)( –sinx) + 2cosx = (2х – 1)sinx.
Приравниваю значение производной функции к нулю и решаю уравнение: (2х – 1)sinx = 0
2х – 1= 0 sinx = 0
х = 0,5 x = 0
Отмечаю точки на чертеже и определяю знаки промежутков. Синус на промежутке 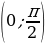 положителен, поэтому определяю знаки первой скобки:
положителен, поэтому определяю знаки первой скобки:
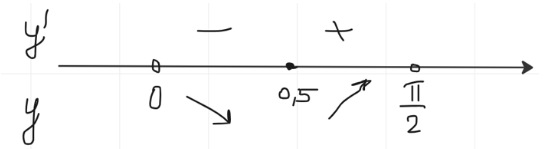
Точка минимума = 0,5.
Ответ: 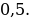
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите точку минимума функции у = (3 – 2х)cosx + 2sinx + 4, принадлежащую промежутку 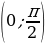 .
.
2) Найдите точку минимума функции у = (6 – 4х)cosx + 4sinx + 4, принадлежащую промежутку 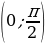 .
.
3) Найдите точку минимума функции у = (1 – 2х)cosx + 2sinx + 3, принадлежащую промежутку 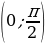 .
.
ТИП №7. Найдите точку минимума функции у = (10 – х)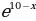 .
.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Т.к. у нас дано произведение двух функций, то считаем производную функции по формуле производной произведения функций.
у΄ = –1 ∙ 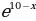 + (10 – х) ∙ (–1)
+ (10 – х) ∙ (–1)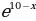 = (–1 – 10 + х)
= (–1 – 10 + х)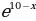 = (х – 11)
= (х – 11)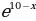 .
.
Приравниваю значение производной функции к нулю и решаю уравнение: (х – 11)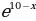 = 0
= 0
х = 11
Ответ: 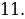
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите точку минимума функции у = (25 – х)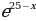 .
.
2) Найдите точку минимума функции у = (16 – х)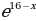 .
.
ТИП №8. Найдите наименьшее значение функции у = 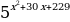 .
.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Поскольку функция у = 2х возрастающая, заданная функция достигает наименьшего значения в той же точке, в которой достигает наименьшего значения выражение
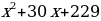 . Квадратный трёхчлен у =
. Квадратный трёхчлен у = 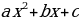 с положительным старшим коэффициентом достигает значения в точке:
с положительным старшим коэффициентом достигает значения в точке:
х = 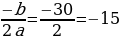
Найдём значение функции в данной точке:
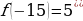
Ответ: 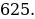
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите наименьшее значение функции у = 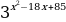 .
.
2) Найдите наименьшее значение функции у = 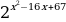 .
.
3) Найдите наименьшее значение функции у = 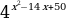 .
.
4) Найдите наименьшее значение функции у = 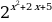 .
.
ТИП №9. Найдите наименьшее значение функции у = 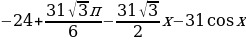 на отрезке
на отрезке 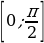 .
.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Т.к. в концах отрезка значения иррациональны, то концы отрезка не рассматриваем. Нахожу производную функции:
у΄ = 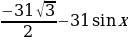 .
.
Приравниваю значение производной функции к нулю и решаю уравнение:
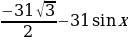 = 0
= 0
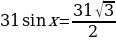
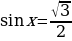
х = 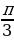 .
.
Считаю значение в полученной точке: 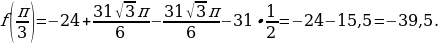
Ответ: 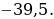
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите наименьшее значение функции у = 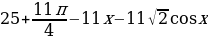 на отрезке
на отрезке 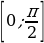 .
.
2) Найдите наименьшее значение функции у = 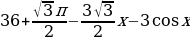 на отрезке
на отрезке 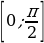 .
.
3) Найдите наибольшее значение функции у = 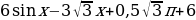 на отрезке
на отрезке 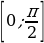 .
.
ТИП №10. В какой точке функция у = 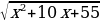 принимает наименьшее значение?
принимает наименьшее значение?
М Е Т О Д И К А Р Е Ш Е Н И Я.
Задания данного типа решаются логически.
Чтобы корень из некоторой функции был наименьшим, то и функция должна принимать наименьшее значение.
Функция – парабола. Ветви параболы направлены вверх. Наименьшее значение функция принимает в вершине параболы. Достаточно найти координату вершины.
х = 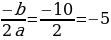
Ответ: 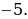
ПОДОБНЫЕ ЗАДАНИЯ:
1) В какой точке функция у = 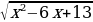 принимает наименьшее значение?
принимает наименьшее значение?
2) В какой точке функция у = 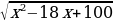 принимает наименьшее значение?
принимает наименьшее значение?
3) В какой точке функция у = 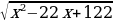 принимает наименьшее значение?
принимает наименьшее значение?
4) В какой точке функция у = 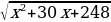 принимает наименьшее значение?
принимает наименьшее значение?
ТИП №11. Найдите точку максимума функции у = 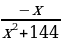 .
.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Нахожу производную функции:
у΄ = 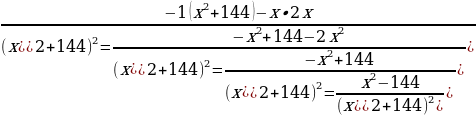 .
.
Приравниваем дробь к нулю (чтобы дробь равнялась нулю, числитель должен равняться нулю):
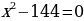
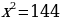
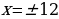
Отмечаю на прямой точки и рассматриваю промежутки:
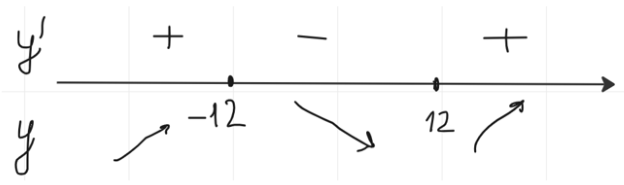
Точка максимума = - 12
Ответ: 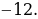
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите точку максимума функции у = 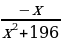 .
.
2) Найдите точку максимума функции у = 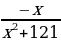 .
.
3) Найдите точку максимума функции у = 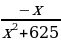 .
.
4) Найдите точку максимума функции у = 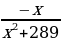 .
.
ТИП №12. Найдите наибольшее значение функции у = 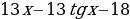 на отрезке
на отрезке 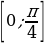 .
.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Проверяю концы отрезка (имеет смысл проверить только 0):
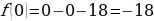 .
.
Нахожу производную функции и приравниваю её к нулю:
у΄ = 13 – 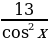
13 – 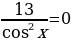
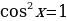
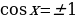
x = 0 (на нашем отрезке)
Ответ: 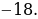
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите наибольшее значение функции у = 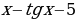 на отрезке
на отрезке 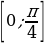 .
.
2) Найдите наибольшее значение функции у = 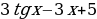 на отрезке
на отрезке 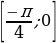 .
.
ТИП №13. Найдите точку максимума функции у = 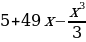 .
.
М Е Т О Д И К А Р Е Ш Е Н И Я.
Нахожу производную функции:
у΄ = 49 – 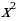 .
.
Приравниваю значение производной функции к нулю:
49 – 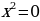
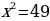
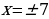
3) Отмечаю данные точки на прямой и рассматриваю промежутки:
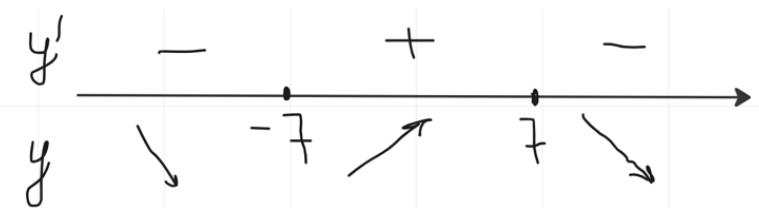
Точка максимума = 7
Ответ: 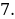
ПОДОБНЫЕ ЗАДАНИЯ:
1) Найдите точку максимума функции у = 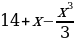 .
.
2) Найдите точку максимума функции у = 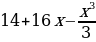 .
.







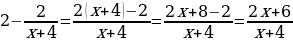 .
.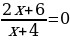
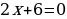
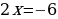
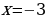
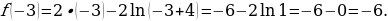
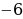 .
.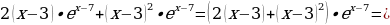
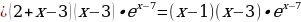
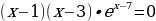

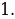
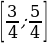 .
.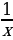
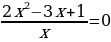
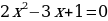
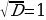 .
.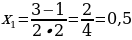 – не принадлежит заданному промежутку
– не принадлежит заданному промежутку 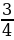 .
. 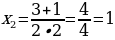 .
.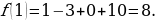
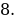
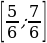 .
.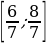 .
.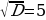 .
.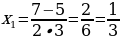
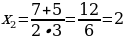 .
.
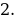
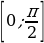 .
.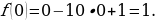
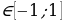 .
. 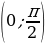 .
.
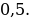
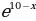 .
.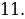
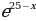 .
.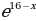 .
.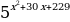 .
.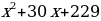 . Квадратный трёхчлен у =
. Квадратный трёхчлен у = 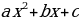 с положительным старшим коэффициентом достигает значения в точке:
с положительным старшим коэффициентом достигает значения в точке: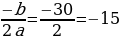
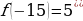
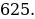
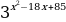 .
.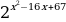 .
.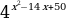 .
.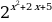 .
.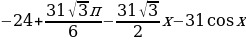 на отрезке
на отрезке 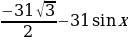 .
.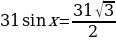
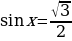
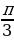 .
.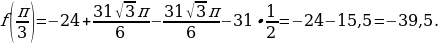
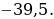
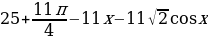 на отрезке
на отрезке 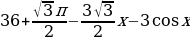 на отрезке
на отрезке 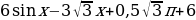 на отрезке
на отрезке 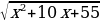 принимает наименьшее значение?
принимает наименьшее значение?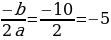
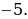
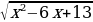 принимает наименьшее значение?
принимает наименьшее значение?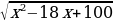 принимает наименьшее значение?
принимает наименьшее значение?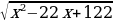 принимает наименьшее значение?
принимает наименьшее значение?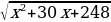 принимает наименьшее значение?
принимает наименьшее значение?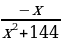 .
.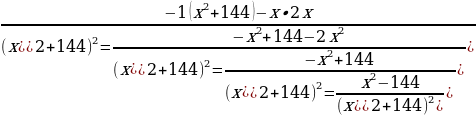 .
.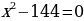
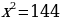
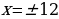

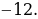
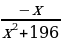 .
.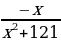 .
.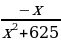 .
.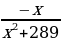 .
.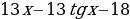 на отрезке
на отрезке 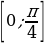 .
.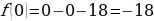 .
.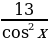
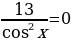
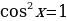
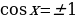
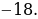
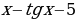 на отрезке
на отрезке 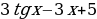 на отрезке
на отрезке 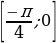 .
.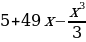 .
.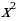 .
.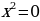
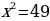
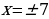

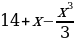 .
.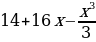 .
.









