Задание 14. Вариант 18. ЕГЭ 2018 из 36 вариантов.

Задание 14. Вариант 18. ЕГЭ 2018 из 36 вариантов.

В правильной четырёхугольной пирамиде SABCD основание ABCD — квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка М так, что AM = 6.

а) Постройте перпендикуляр из точки S на плоскость ВСМ.

б) Найдите расстояние от вершины S до плоскости ВСМ.

Решение.

а) Построим плоскость BCM. Так как плоскость BCM параллельна AD, то она пересекает грань ADS по прямой MN параллельной AD. В результате получаем плоскость, проходящую через точки B, C, M и N (см. рисунок). Опускаем перпендикуляр из точки S на плоскость BCM, который будет располагаться вне пирамиды в точке H (см. рисунок) и лежать на прямой UT.

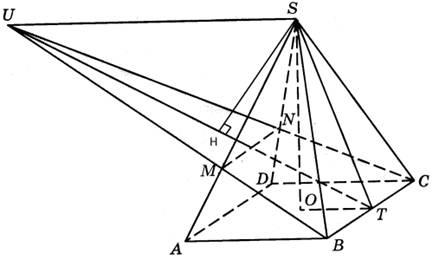
б) Прямые BM и CN пересекаются в точке U, причем прямая US параллельна AB. Докажем это. Рассмотрим две плоскости SAB и SCD, которые пересекаются по прямой SU, причем, линия их пересечения SU будет параллельна основанию пирамиды (следствие из признака параллельности прямой и плоскости). Прямые BU и CU принадлежат плоскостям SAB и SCD, следовательно, они пересекаются в точке U, а сама прямая SU будет параллельна AB. Теперь рассмотрим подобные треугольники USM и BAM, для сторон которых справедливо отношение

,

подставляем числовые значения, получаем

.

Точка T – середина BC. Так как   и  , то плоскость BCM перпендикулярна плоскости UST. То есть SH – это высота треугольника UST. Найдем ее.

Сначала вычислим  . Далее, так как SO – высота пирамиды, то  . По теореме косинусов в треугольнике UST  , при этом  , получаем:

.

Найдем высоту SH из площади треугольника UST:

,

причем площадь можно вычислить как произведение половины стороны US на высоты, проведенной из точки T на нее, но эта высота равна SO, следовательно,

,

откуда

.