Задание 16. Вариант 19 из 36 вариантов ЕГЭ 2021

Задание 16. Вариант 19 из 36 вариантов ЕГЭ 2021

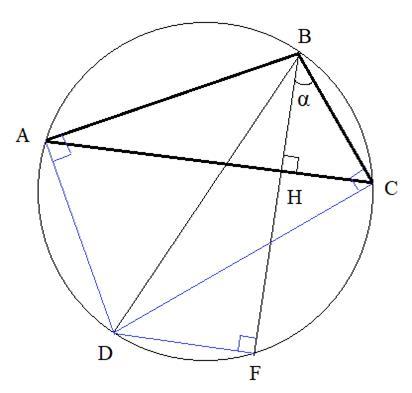
Задание 16. В треугольнике ABC все стороны различны. Прямая, содержащая высоту ВН треугольника ABC, вторично пересекает описанную около этого треугольника окружность в точке F. Отрезок BD — диаметр этой окружности.

а) Докажите, что АВ = CF.

б) Найдите DF, если радиус описанной около треугольника ABC окружности равен 12,  угол BAC = 35°, угол ACB = 65°.

Решение.

а) Угол BCD – вписанный и опирается на диаметр окружности, значит, он равен 90°. Далее, пусть , тогда . Учитывая, что , . Получаем: , откуда следует, что дуги  и, следовательно, CF=AD.

б) Угол , тогда  (так как дуги AD=CF, см. п. а) и . Из треугольника ABC найдем угол ABC:

Значит,

Учитывая, что треугольник DBF прямоугольный с гипотенузой DB=2∙12=24 и углами 30° и 60°, катет DF, лежащий против угла в 30°, равен:

Ответ: 12.

Задание 13. а) Решите уравнение .

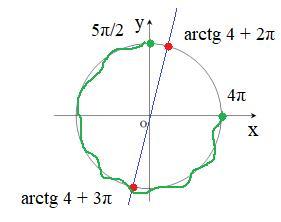
б) Найдите все корни этого уравнения, принадлежащие промежутку [5π/2; 4π].

Решение.

а) Преобразуем выражение:

Далее, переходим к равенству степеней:

Разделим обе части уравнения на , получим:

Пусть , имеем:

Обратная подстановка дает два уравнения:

б) Вычислим корни уравнения, принадлежащие промежутку [5π/2; 4π]. Для первого корня

Имеем один корень . Для второго корня получаем значение

Ответ: а) ; ; б)