Задание 16. Вариант 2 ЕГЭ 2021 из 36 вариантов

Задание 16. Вариант 2 ЕГЭ 2021 из 36 вариантов

Задание 16. Две окружности разных радиусов касаются внешним образом в точке С. Вершины А и В равнобедренного прямоугольного треугольника ABC с прямым углом С лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.

а) Докажите, что прямые AD и BE параллельны.

б) Найдите ВС, если радиусы окружностей равны √15 и 15.

Решение.

а)Две окружности разного радиуса касаются внешним образом в точке C, причем  , AC = BC. Также  , так как AD – диаметр первой окружности и  , так как BE–диаметр второй окружности. Далее, O1D = O1C как радиусы, значит,  ,  (как вертикальные),  (так как треугольник BCO2 –равнобедренный). Следовательно,  . Эти же углы являются накрест лежащими для прямыхAD, BE и секущей BD. Значит,   по признаку параллельности прямых.

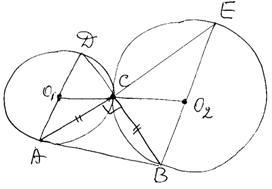
б)По условию задания  , тогда  . Рассмотрим прямоугольный треугольник ACD. Пусть CD = x, AC = y. Тогда:

Рассмотрим подобные треугольники BCE и DCA (по двум углам), для которых запишем отношение:

Значит,  . По условию задания AC = CB, следовательно,   и

И отрезок BC, равен:

Ответ: 7,5