Задание 16. Вариант 3 ЕГЭ из 10 вариантов 2021

Задание 16. Вариант 3 ЕГЭ из 10 вариантов 2021

В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин — точка О.

а) Докажите, что около четырёхугольника ABCD можно описать окружность.

б) Найдите радиус вписанной окружности, если АС = 10, BD = 26.

Решение.

а)В четырехугольнике ABCD диагонали AC и BD взаимно перпендикулярны, следовательно,

Пусть (так как треугольники ABO и CBO подобны по условию задания). Также  и  из подобия треугольников CBO и DCO. Причем должно выполняться условие: . Наконец, из подобия треугольников DCO и DAO следует, что . Имеем:

Из последних двух равенств следует, что вокруг четырехугольника ABCD можно описать окружность.

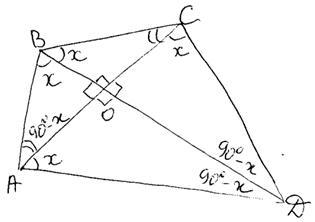
б)Рассмотрим равнобедренный треугольник ABC с биссектрисой BO, следовательно, она же является и высотой и медианой, поэтому AO=OC=5. Учитывая, что

треугольник BCD – прямоугольный с высотой CO. Пусть BO = x, тогда OD = 26-x и

Решаем квадратное уравнение, получаем два корня:

Следовательно, BO = 1, OD = 25 или, наоборот, BO = 25, OD = 1. Предположим, что BO = 1, OD = 25, тогда:

Для второго варианта: . Так как AB = BC, AD = CD, то периметр четырехугольника ABCD, равен:

Площадь четырехугольника ABCD:

И также ее можно определить по формуле:

Ответ: