Задание 16. Вариант 30 из 36 вариантов ЕГЭ 2021

Задание 16. Вариант 30 из 36 вариантов ЕГЭ 2021

Задание 16. Дан прямоугольный треугольник ABC с прямым углом С. На катете АС взята точка М. Окружность с центром О и диаметром СМ касается гипотенузы в точке N.

а) Докажите, что прямые MN и ВО параллельны.

б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM : МС = 1:3.

Решение.

а) Касательная к окружности перпендикулярна ее радиусам в точке касания, то есть, треугольники OCB и ONB – прямоугольные. Кроме того, треугольники OCB и ONB равны по катету (OC=ON как радиусы) и гипотенузе OB (общая). Следовательно, углы 1 и 2 также равны и это значит, что дуги CF и NF, на которые они опираются, тоже равны.

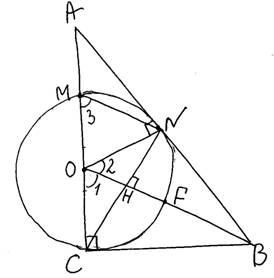
Угол CMN – вписанный и опирается на дугу CN и равен половине ее градусной меры. Получаем, что   (см. рисунок) и   по признаку параллельных прямых.

б) Пусть x – коэффициент пропорциональности. По условию задания AM:MC=1:3, то есть, AM=x, а MC=3x. Также MC – диаметр окружности, поэтому, MO=CO=1,5x (радиусы окружности).

Рассмотрим подобные треугольники ACB и ANO (подобны по двум углам:  , угол A – общий). Для подобных треугольников можно записать следующее отношение:

,

откуда

.

По теореме об отрезках касательных, имеем:

CB = BN = 3x.

Рассмотрим прямоугольный треугольник ABC, в котором  . Тогда из треугольника CNB по теореме косинусов, получаем:

В результате, имеем:

Рассмотрим подобные треугольники AOB и AMN (так как  ). Запишем следующее отношение:

Рассмотрим равнобедренный треугольник NOC (так как OC = ON – радиусы окружности), в котором OH – биссектриса, а значит, и высота и медиана, то есть,   и NH = CH = 2, NH – высота трапеции MNBO. Найдем площадь трапеции MNBO:

Ответ: 7.