Задание 16. Вариант 4 ЕГЭ 2021 из 36 вариантов

Задание 16. Вариант 4 ЕГЭ 2021 из 36 вариантов

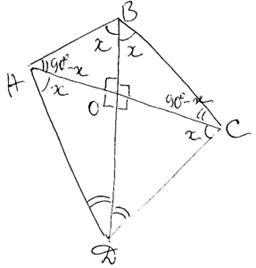
Задание 16. В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке О под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин — точка О.

а) Докажите, что в четырёхугольник ABCD можно вписать окружность.

б) Найдите радиус вписанной окружности, если АС = 12, BD = 13.

Решение.

а)В четырехугольнике ABCD диагонали AC и BD взаимно перпендикулярны и пересекаются в точке O, следовательно,

Пусть  (так как треугольники ABO и CBO подобны по условию задания). Так как  , то   и  . Так как треугольники BCOи COD подобны, то  . Так как треугольники OCDи OADподобны, то  . Треугольники ABC и ADC – равнобедренные со сторонами AB = BC и AD = DC. Следовательно,

AB+CD = BC+AD

и это означает, что в четырехугольник ABCD можно вписать окружность.

б)Радиус r вписанной окружности можно найти из площади четырехугольника ABCD:

где P – периметр четырехугольника ABCD. Отсюда следует, что

Рассмотрим равнобедренный треугольник ABC с биссектрисой OB, которая также является его высотой и медианой. Следовательно, AO=OC=6. Рассмотрим прямоугольный треугольник BCD с прямым углом  . Следовательно, CO – высота. Пусть BO = y, тогда OD=13-yи

Решаем квадратное уравнение, получаем корни:

То есть, BO=4, OD = 9 или, наоборот, BO=9, OD=4. Возьмем первый вариант. Тогда:

Следовательно,  . Получаем периметр и площадь четырехугольника ABCD:

И радиус вписанной окружности, равен:

Ответ: