Задание 19.Вариант 21 из 36 вариантов ЕГЭ 2017

Задание 19.Вариант 21 из 36 вариантов ЕГЭ 2017

Задание 19. Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 14 раз больше, либо в 14 раз меньше предыдущего. Сумма всех членов последовательности равна 7424.

а) Может ли последовательность состоять из двух членов?

б) Может ли последовательность состоять из трёх членов?

в) Какое наибольшее количество членов может быть в последовательности?

Решение.

а) Число 7424 при разложении на простые множители дает

.

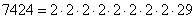Предположим, что последовательность состоит из двух членов. Если обозначим через a наименьшее число, то набольшее будет равно 14a. Получаем уравнение

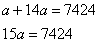
Как видим, числа 15 и 7424 взаимно простые, т.к. 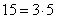  не содержит множителей из 7424, а значит уравнение неразрешимо в целых значениях.

Ответ: нет.

б) Для трех членов имеем уравнение вида

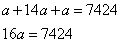
и число 16 при разложении на простые множители дает

,

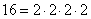является делителем числа 7424, следовательно, последовательность может состоять из трех членов, например,

.

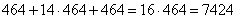Ответ: да.

в) Число 7424 можно представить в виде

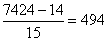
это означает, что его можно представить в виде сумм чисел

(14+1)+(14+1)+...

с последним значением 14. Таким образом, общее число членов будет равно  .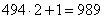

Ответ: 989.