№5
Задание 1.
У исполнителя РОБОТ две команды, которым присвоены номера:
1. Движение вниз на две клетки.
2. Движение влево на b клетку.
Выполняя первую из них, РОБОТ снижается на 2 клетки, а выполняя вторую, уходит влево на b клетку(ки). Программа для исполнителя РОБОТ — это последовательность номеров команд. Известно, что программа 21212 переводит РОБОТА в пункт назначения (крестик). Определите значение b.

Задание 2.
Вам необходимо написать программу, по которой компьютер нарисует змею.
Компьютер знает несколько команд, вот их список:
1. Вверх на две клетки.
2. Вправо на две клетки.
3. Вниз на две клетки.
4. Влево на две клетки.
5. Уменьшить предыдущую команду в два раза (Например: комбинация 1,5 будет считаться как «вверх на одну клетку).
Если написать, например, «1,1,5.», то компьютер нарисует линию в три клетки вверх.
Начинайте с команды №1. (Глаз змеи рисовать компьютеру не нужно).
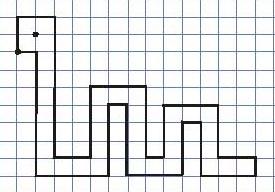
Ответ: 1, 2, 3,3,3,3, 2, 1,1, 2,2,5, 3,3, 2,5, 1,1,5, 2,2,5, 3,3,5, 2, 3,5, 4,4,5, 1,1,5, 4,5, 3,3,5, 4,4,5, 1,1, 4,5, 3,3, 4,4, 1,1,1,1,5, 4,5. (Я отделил пробелами каждую сторону змеи)
Задание 3.
В компьютере сломалась функция отрисовки маршрута, у нас имеется только начало пути, конец и программа, по которой необходимо двигаться, вот маршрут:

Вам необходимо указать в какой из красных точек окажется «Ева», если начнёт двигаться из зелёной точки по указанной программе-алгоритму.
Сама программа закодирована в восьмизначной системе счисления, где:
1 – движение вверх на две клетки
2 – движение вниз на две клетки
3 – движение вправо на две клетки
4 – движение влево на две клетки
Программа выглядит так:
4,4, 1, 3, 1, 4, 1,1, 3, 1, 3,3, 2, 3. (Для удобства я разделил пробелами и запятыми, иначе бы она выглядела так: «44131411313323» – это было бы неудобно).
Задание 4.
Теперь вам нужно самому составить путь к точке, но на карте существуют магнитные поля, в которых робот «Ева» выключается и не может продолжать свой путь, поэтому вам нужно объезжать эти поля. Начало магнитных полей отмечены жёлтым, а сами магнитные поля обозначены значками «магнитами». Ева может ездить только по сторонам клеток. Если силуэт (диаметр зелёной точки) Евы касается магнитного поля, то Ева выходит из строя.

Ева

Сама программа должна быть закодирована в восьмизначной системе счисления, где:
1 – движение вверх на две клетки
2 – движение вниз на две клетки
3 – движение вправо на две клетки
4 – движение влево на две клетки
Пример: 1,2,4,1,3.
Задание 5.
У меня закончилась фантазия, пускай это будет таблица с пропусками.
У исполнителя Делитель две команды, которым присвоены номера:
1. раздели на 2
2. вычти 1
Первая из них уменьшает число на экране в 2 раза, вторая уменьшает его на 1. Исполнитель работает только с натуральными числами. Составьте алгоритм получения из числа 65 числа 4, содержащий не более 5 команд. В ответе запишите только номера команд.
Начало – 65.
| Номер команды | Номер необходимой операции (1 или 2) | Получившийся результат |
| 1 | ? | 64 |
| 2 | 1 | ? |
| 3 | ? | 16 |
| 4 | 1 | ? |
| 5 | ? | 4 |
Необходимо вместо «?» вставить необходимый ответ, чтобы из числа 65 получилось число 4.
Ответ: 1) 2 2) 32 3) 1 4) 8 5)1
№10
Задание 1.
Число 111010002 (в двоичной системе счисления). Оно переводится в десятичную систему счисления по следующей схеме.
Каждый отдельный символ в этом числе умножается на число, которое соответствует системе счисления в степени, соответствующей порядковому номеру числа (Примечание: начинается с 0, расставляются справа-налево). Например:

По такой же схеме переведите число 10101111 в десятичную систему счисления.
Ответ: 17510
Задание 2.
Для перевода из любой системы счисления в двоичную систему счисления необходимо произвести деление этого числа на 2.

Записываем в обратном порядке, как показано на рисунке.
А теперь задание: переведите число 57110 в двоичную систему счисления.
Ответ: 10001110112
Задание 3.
Известный факт, что века считаются римскими цифрами, так, например сейчас 21 век, записывается римскими цифрами, как «XXI».
В «римской системе счисления» некоторые цифры обозначаются так:
1 – I (Если например требуется 2 или 3, то палочки увеличиваются, то есть 2-II, 3-III)
5 – V (Если необходимо написать 4, то пишется IV. Это значит, что у 5 отнимается 1)
10 – X (Если необходимо написать 8, то это можно сделать 2 путями: 1) VIII; 2) IIX)
100 – C
500 – D
1000 – M
И так далее. В моём задании вам необходимо вспомнить даты событий и написать их век римскими цифрами. Помните, что век считается после прошествии 100 лет, то есть время с 1 января 1901 года по 31 декабря 2000 года всё ещё считается 20 веком.
1. Распад СССР
2. Отмена крепостного права в России
3. Правление Ивана Грозного
4. Крещение Руси
5. Гибель Римской империи
Ответ: 1) XX 2) IXX 3) XVI 4) X 5) V
Задание 4.
Вам необходимо перевести римские числа в привычные нам. То есть перевести из «римской системы счисления» в привычную нам десятичную.
DC; 2) CM; 3) XC?
Ответ: 1) 600; 2) 900; 3) 90.
Задание 5.
В двоичной системе счисления существуют всего 2 числа: 0 и 1. Если мы сложим их, то получится следующее: 0+1=1. Если мы сложим две единицы: 1+1=? – мы не можем написать 2, так как такого символа не существует в двоичной системе счисления, поэтому нам следует писать так: 1+1=10. Далее если мы прибавим к 10 1, то получится 11: 10+1(или 01)=11. Каждый раз, когда разрядные единицы заполняются максимальными значениями системы счисления, то разрядные единицы увеличиваются: единицы, десятки и единицы, сотни, десятки и единицы и т.д.

А теперь составьте таблицы сложения:
В пятеричной системе счисления;
В троичной системе счисления.
Примечание: достаточно лишь сложить единицы. Десятки, сотни и прочее не нужно складывать.
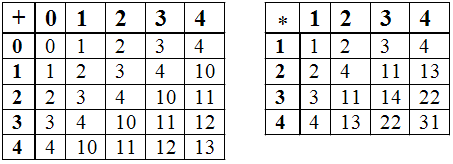
Ответ:
1) 
2) 



























