Задания с параметрами в учебнике 10 класса (авторы учебника: Алимов Ш.А., Колягин Ю.М., Ткачева М.В., Федорова Н.Е., Шабунин М.И.)
Десятиклассники завершают изучение традиционных тем алгебры, что дает возможность решать всевозможные уравнения и неравенства, в том числе и по темам, которые изучались в основной школе, и готовит почву для изучения начал математического анализа в 11 классе.
В учебнике 10 класса встречаются следующие задания с параметрами:
Уравнения:
– линейные уравнения (№ 1322, № 1323);
– квадратные уравнения (№ 1396, № 1397)
– логарифмические уравнения (№ 353);
– тригонометрические уравнения (№ 646, 647, 687, 688, 689, 1605).
Системы уравнений:
– система логарифмических уравнений (№ 1569);
– система уравнений, одно из которых тригонометрическое (№ 1570, № 1609).
Неравенства:
дробно-рациональные неравенства (№ 1611);
неравенства с модулем (№ 1579);
иррациональные неравенства (№ 191)
логарифмические неравенства (№ 406, № 1616).
Многие из приведенных номеров могут использоваться для систематического повторения курса алгебры, поэтому приведены в разделах «Упражнения для итогового повторения курса алгебры и начал математического анализа», «Задачи для внеклассной работы». Некоторые задания доступны для решения учащимися основной школы и могут быть предложены способным учащимся 8-9 классов.
У
№ 1322. При каком значении а, уравнение а(х – 3) + 8 = 13 (х + 2) имеет корень, равный 0?
равнения
?
Решение
Корень уравнения обращает его в верное равенство. Подставим х = 0 в уравнение, получим:
а (–3) + 8 = 13.2,
–3а = 18,
а = –6.
Ответ: –6.
Задание для самостоятельного решения
№ 1323. При каком значении b уравнение 1 – b (x + 4) = 2 (x – 8) имеет корень, равный 1?
О
№ 1396. При каком наименьшем целом значении m уравнение (m – 1) x2 – 2 (m + 1) x + m – 3 = 0 имеет два различных действительных корня?
твет:
b = 3.
?
Решение
При m = 1 уравнение является линейным и не может иметь два корня. Рассмотрим случай m 1. Квадратное уравнение имеет два различных действительных корня, если дискриминант уравнения положительный.

 .
.
Наименьшее целое число, большее числа  и не равное 1 – это 2.
и не равное 1 – это 2.
Ответ: 2.
Задания для самостоятельного решения
№ 1397. При каких целых значениях m уравнение (m – 7)x2 + 2(m – 7)x + 3 = 0 не имеет действительных корней?
Ответ: 8, 9.
№ 353. Найти все значения параметра а, при которых уравнение  имеет корни.
имеет корни.
?
Решение
ОДЗ: х 0, a 0, a 1.

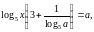

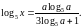
Выражение имеет смысл при 
Ответ: а 0, a 1,  .
.
№ 646. Найти все значения а, при которых уравнение  имеет корни, и решить это уравнение.
имеет корни, и решить это уравнение.
?
Решение



Имеем: 4t2 – 2(a – 3)t – 3a = 0;
D1 = (a – 3)2 + 12a = a2 – 6a + 9 + 12a = (a + 3)2 0 для любых значений а.

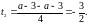
1)  . Уравнение имеет корни, только если
. Уравнение имеет корни, только если  ,
,  .
.

2)  . Уравнение не имеет корней.
. Уравнение не имеет корней.
Ответ: при а a 2 корней нет,
при  корни
корни  .
.
№ 647. Найти все значения а, при которых уравнение  не имеет корней.
не имеет корней.
?
Решение
Воспользуемся формулами понижения степени, получим:



Введем вспомогательный угол, разделив обе части на  .
.
 .
.
Уравнение не имеет корней, если




Ответ:  или
или  .
.
№ 688. Найти все значения а, при которых уравнение  имеет корни.
имеет корни.
?
Решение

Воспользуемся формулой (а + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5:


Пусть  , 0 t 1.
, 0 t 1.
5t2 + 10t + 1 – 16a = 0;

Уравнение имеет корни, если 20 + 80а 0, то есть а –0,25. Тогда

Учитывая ограничения на t, получим:



Из первого неравенства  , что удовлетворяет условию а –0,25. Второе неравенство решений не имеет.
, что удовлетворяет условию а –0,25. Второе неравенство решений не имеет.
Ответ:  .
.
Задания для самостоятельного решения
№ 687. При каких значениях а уравнение  имеет корни? Найдите эти корни.
имеет корни? Найдите эти корни.
Ответ:
№ 1605. Найти все значения а, при которых уравнение  имеет корни, и решить это уравнение.
имеет корни, и решить это уравнение.
О
№ 689. Найти все значения а, при которых уравнение имеет корни, и решить это уравнение.
твет:
?
Решение
Воспользовавшись формулами приведения и двойного угла, учитывая четность функции y = cos x, получим:
.
Преобразуем выражение и подставим в уравнение. Получим:
Разделив обе части уравнения на 2 и заменив  , получим:
, получим:

 уравнение имеет корни.
уравнение имеет корни.

 .
.
1) Если  то есть
то есть  , то
, то 
.
2) Если  , то есть
, то есть  , то
, то 
.
Таким образом, если  или
или  , то
, то
,
если  , то
, то
и .
Если а a 1, уравнение решений не имеет.
Ответ: при  и
и 
при  ,
,
Системы уравнений
№ 1569 (1). Решить систему уравнений и установить, при каких значениях параметра а она имеет решение:
?
Решение
ОДЗ: х 0, y 0, x 1, y 1.
Решим первое уравнение системы:




Получаем две системы уравнений.


Решим второе уравнение системы:



 , при этом a 0, –a – 1 0.
, при этом a 0, –a – 1 0.




Воспользуемся результатом решения предыдущего уравнения:


Получим совокупность:


Учитывая условия х 0, y 0, x 1, y 1, получим ряд ограничений:
a 0;
a 1;
–a – 1 0, a ;
–a – 1 1, a –2.
Итак, если a 0 и a 1, решениями являются пары  и
и  .
.
Если a a –2, решениями являются пары  и
и  . В остальных случаях решений нет.
. В остальных случаях решений нет.
Ответ: при a 0, a 1  ,
,
при a a –2  ,
, 
Задания для самостоятельного решения
№ 1569 (2) Решить систему уравнений и установить, при каких значениях параметров а и b она имеет решение:

О
?
твет:

,

при
b 0,
b 1,

№ 1570. Для всех значений параметра а решить систему уравнений
имеет хотя бы одно решение?
Решение
Представим второе уравнение системы в виде
Все слагаемые неотрицательны, значит,







 (верно).
(верно).
Проверим, является ли решение второго уравнения (0; 1) при а = 3 решением системы, подставив значения в первое уравнение системы:
9 – 6 – 1 – 2 = 0 (верно).
Проверим, является ли пара (0; 1) решением второго уравнения при 



Уравнение решений не имеет.
Итак, при а = 3 система имеет решение, при а3 решений нет.
Ответ: при а = 3 решение (0; 1);
при а 3 решений нет.
№ 1609. При каких значениях а система уравнений
имеет хотя бы одно решение?
?
Решение
Область допустимых значений: y 3, x 0.
Решим первое уравнение системы:



 .
.

Решим второе уравнение системы:



По условию система должна иметь хотя бы одно решение, поэтому рассмотрим два случая:
1)  .
.
 .
.
Тогда 
Убеждаемся, что  , значит, система имеет решение
, значит, система имеет решение 
2)  .
.


Проверим, какие значения  удовлетворяют области допустимых значений.
удовлетворяют области допустимых значений.
1) 




Итак, 
2) 


Итак, 
Окончательно получаем  .
.
Ответ:  .
.
Неравенства
№ 1611 (1). Найти все значения а, при которых является верным при всех значениях х неравенство:

?
Решение
Квадратный трехчлен, находящийся в знаменателе дроби, имеет отрицательный дискриминант, положительный первый коэффициент, поэтому знаменатель не обращается в 0 при любых х.

.
В случае если 8 – 4а = 0, то есть а = 2, неравенство 0х2 + 0х + 3 – 2 0 решений не имеет.
При а 2 неравенство является верным при всех значениях х, если первый коэффициент отрицательный и дискриминант квадратного трехчлена неположительный, то есть

Уравнение  имеет корни
имеет корни

Имеем систему неравенств:




Ответ: 
Задания для самостоятельного решения
№ 1611 (2) Найти все значения а, при которых является верным при всех значениях х неравенство 
Ответ: 
№ 1579. При всех а решить неравенство  и указать все значения а, при которых решения этого неравенства являются решениями неравенства x2 – 4х – 5
и указать все значения а, при которых решения этого неравенства являются решениями неравенства x2 – 4х – 5
?
Решение
Рассмотрим различные случаи в зависимости от знака выражения, стоящего под знаком модуля.
1) Пусть x 5a, x – 5a 4a – 3, x 9a – 3.
a) 9a – 3 = 5a, 4a = 3,  , тогда неравенство имеет решение
, тогда неравенство имеет решение 
б) 9a – 3 5a, 4a 3,  , тогда 5а х 9а – 3;
, тогда 5а х 9а – 3;
в) 9a – 3 a,  , решений нет.
, решений нет.
2) Пусть x a, –x + 5a 4a – 3, x a + 3.
a) 5a a+ 3, 4a 3,  , тогда a + 3 x a;
, тогда a + 3 x a;
б) 5a a+ 3,  , нет решений.
, нет решений.
Итак, если  , решений нет, если
, решений нет, если  , то
, то  , если
, если  , то
, то
а + 3 х 9а – 3.
Рассмотрим неравенство x2 – 4х – 5
(х – 5)(х + 1) x
Решения первого неравенства являются решениями второго, если



Ответ: если  , решений нет;
, решений нет;
если  , то
, то  ;
;
если  , то а + 3 х 9а – 3.
, то а + 3 х 9а – 3.
Решения первого неравенства являются решениями второго, если  .
.
№ 191 (1). При различных значениях а решить неравенство 
?
Решение
ОДЗ:  х 6.
х 6.
При х = 6 левая часть неравенства принимает наименьшее значение, то есть 
Таким образом, если а 2, то неравенство не имеет решений.
Пусть а 2. Обе части неравенства неотрицательные, возведем их в квадрат.





Учитывая ОДЗ, получим  .
.
Ответ: при а 2 решений нет;
при а 2  .
.
Задания для самостоятельного решения
№ 191 (2) При различных значениях а решить неравенство 
Ответ: при а 0 
при а = 0 решений нет.
№ 406. Решить неравенство 
?
Решение
ОДЗ: 

а 1.
Введем замену  . Получим:
. Получим:





Если а 1, то 
Если 0 a
Ответ: при а 1  ;
;
при 0 a .
Задания для самостоятельного решения
№ 1616. Найти все значения а, при которых неравенство  выполняется для всех х из промежутка (–; 0).
выполняется для всех х из промежутка (–; 0).
Ответ:  .
.








 .
. и не равное 1 – это 2.
и не равное 1 – это 2. имеет корни.
имеет корни.
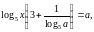

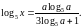

 .
. имеет корни, и решить это уравнение.
имеет корни, и решить это уравнение.



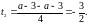
 . Уравнение имеет корни, только если
. Уравнение имеет корни, только если  ,
,  .
.
 . Уравнение не имеет корней.
. Уравнение не имеет корней. корни
корни  не имеет корней.
не имеет корней.










