Задание 20.1 (Робот)

1. Выполните задание.

На бесконечном поле имеется лестница. Сначала лестница спускается вниз справа налево, затем спускается вниз слева направо. Высота каждой 
ступени – одна клетка, ширина – две клетки. Робот находится справа от верхней ступени лестницы.

Количество ступенек, ведущих влево, и количество ступенек, ведущих вправо, неизвестно.

На рисунке указан один из возможных способов расположения лестницы и Робота (Робот обозначен буквой «Р»).

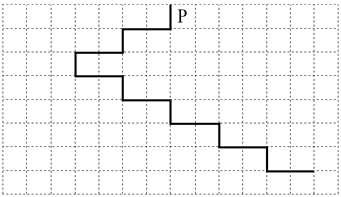
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно над ступенями лестницы, спускающейся слева направо. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок):

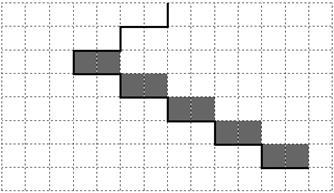
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения ступеней внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

Алгоритм может быть выполнен в среде формального исполнителя или  записан в текстовом редакторе.

Сохраните алгоритм в текстовом файле. Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

1. Выполните задание.

На бесконечном поле имеются две горизонтальных стены, соединенных лестницей. Верхняя стена бесконечно продолжается влево, нижняя - вправо. Количество ступеней лестницы неизвестно. Высота каждой ступени 2 клетки, ширина - 3 клетки. Робот находится на нижней горизонтальной стене, правее лестницы.

На рисунке указан один из возможных способов расположения лестницы, стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий клетки, расположенные рядом с вертикальной частью каждой ступени. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок):

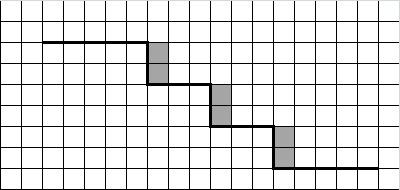
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого количества ступеней.

При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе.

Сохраните алгоритм в текстовом файле. Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

1. Выполните задание

Робот находится в верхней клетке узкого вертикального коридора. Ширина коридора – одна клетка, длина коридора может быть произвольной. Возможный вариант начального расположения Робота приведён на рисунке (Робот обозначен буквой «Р»):

Напишите для Робота алгоритм, закрашивающий все клетки внутри коридора и возвращающий Робота в исходную позицию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок):

Алгоритм должен решать задачу для произвольного конечного размера коридора. При исполнении алгоритма Робот не должен разрушиться.

Алгоритм может быть выполнен в среде формального исполнителя или  записан в текстовом редакторе.

Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

1. Выполните задание.

На бесконечном поле имеются четыре стены, соединённые между собой, которые образуют прямоугольник. Длины стен неизвестны. В левой вертикальной стене есть ровно один проход, в нижней горизонтальной стене также есть ровно один проход. Проход не может примыкать к углу прямоугольника. Точные места проходов и ширина проходов неизвестны. Робот находится около нижнего конца левой вертикальной стены, снаружи прямоугольника и выше нижней стены.

На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные вдоль стен прямоугольника с внутренней стороны. Проходы должны остаться незакрашенными. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера прохода внутри стены.

Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле. Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

1. Выполните задание.

На бесконечном поле имеются две одинаковые вертикальные стены и одна горизонтальная, соединяющая верхние концы стен. Длины стен неизвестны. Робот находится в одной из клеток, расположенных между нижними краями  вертикальных стен.

На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).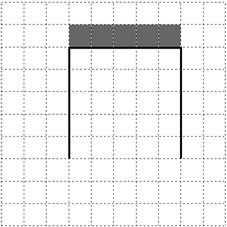

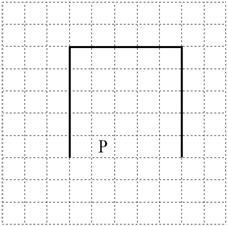
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные выше горизонтальной стены непосредственно над ней. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

1. Выполните задание.

На бесконечном поле имеется вертикальная стена. Длина стены неизвестна. От верхнего конца стены вправо отходит горизонтальная стена также неизвестной длины. От правого конца этой стены отходит вниз вторая вертикальная стенанеизвестной длины. Робот находится в клетке, расположенной справа от нижнего края первой вертикальной стены.

На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»):

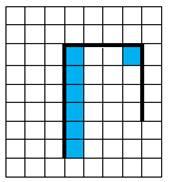
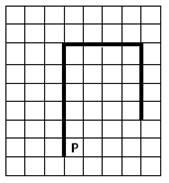
Напишите для Робота алгоритм, закрашивающий клетки, расположенные правее первой вертикальной стены, и угловую клетку, расположенную на пересечении горизонтальной и второй вертикальной стены. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок):

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться.

1. Выполните задание.

Робот находится в левом верхнем углу огороженного пространства, имеющего форму прямоугольника. Размеры прямоугольника неизвестны. Где-то посередине прямоугольника есть вертикальная стена, разделяющая прямоугольник на две части. В этой стене есть проход, при этом проход не является самой левой или самой нижней клеткой стены. Точное расположение прохода также неизвестно. Одно из возможных расположений стены и прохода в ней приведено на рисунке (робот обозначен буквой «Р»):

Напишите для робота алгоритм, перемещающий робота в правый нижний угол прямоугольника (см. рисунок):

Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться.

Алгоритм может быть выполнен в среде формального исполнителя или  записан в текстовом редакторе.

Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

1. Выполните задание.

На бесконечном поле имеется стена, состоящая из 5 последовательных отрезков, расположенных змейкой: вправо, вниз, влево, вниз, вправо, все отрезкинеизвестной длины. Робот находится в клетке, расположенной снизу от левого края первой горизонтальной стены.

На рисунке указан один из возможных способов расположения стен

и Робота (Робот обозначен буквой «Р») .

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные ниже первого и левее второго отрезков стены и левее четвертого и ниже пятого отрезков стены и угловой клетки. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок)

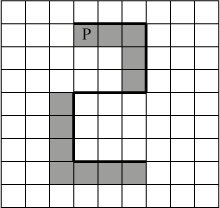
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться.

Алгоритм может быть выполнен в среде формального исполнителя или  записан в текстовом редакторе.

1. Выполните задание.

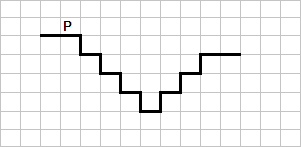
На бесконечном поле имеется лестница. Сначала лестница справа налево спускается вниз, затем поднимается вверх. Высота каждой ступени – одна клетка, ширина – две клетки. Робот находится на правой ступеньке лестницы, в правой клетке.

Количество ступеней, ведущих вниз, и количество ступеней, ведущих вверх, неизвестно.

На рисунке указан один из возможных способов расположения лестницы и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно над ступенями лестницы. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок):

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения ступеней поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

Алгоритм может быть выполнен в среде формального исполнителя или  записан в текстовом редакторе.

Сохраните алгоритм в текстовом файле. Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

10. Выполните задание.

На бесконечном поле имеется лестница. Сначала лестница слева направо поднимается вверх, затем спускается вниз. Высота каждой ступени – две клетки, ширина – одна клетка. Робот находится на нижней ступеньке лестницы слева.

Количество ступенек, ведущих вверх, и количество ступенек, ведущих вниз, неизвестно.

На рисунке указан один из возможных способов расположения лестницы и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно над ступенями лестницы. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок):

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

Алгоритм может быть выполнен в среде формального исполнителя или  записан в текстовом редакторе.

Сохраните алгоритм в текстовом файле. Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

1. Выполните задание

Робот находится в левой клетке узкого горизонтального коридора. Ширина коридора – одна клетка, длина коридора может быть произвольной. Возможный вариант начального расположения Робота приведён на рисунке (Робот обозначен буквой «Р»):

Напишите для Робота алгоритм, закрашивающий все клетки внутри коридора и возвращающий Робота в исходную позицию. Например, для привёденного выше рисунка Робот должен закрасить следующие клетки (см. рисунок):

Алгоритм должен решать задачу для произвольного конечного размера коридора. При исполнении алгоритма Робот не должен разрушиться.

Алгоритм может быть выполнен в среде формального исполнителя или  записан в текстовом редакторе.

Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

1. Выполните задание.

На бесконечном поле имеется лестница. Сначала лестница спускается вниз слева направо, потом поднимается вверх также слева направо. После подъема лестница переходит в вертикальную стену. Высота каждой ступени 1 клетка, ширина – 1 клетка. Количество ступенек, ведущих вверх, и количество ступенек, ведущих вниз, неизвестно. Между спуском и подъемом ширина площадки 1 клетка.

Робот находится в клетке, расположенной в начале спуска.
На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно над лестницей, как показано на рисунке. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для бесконечного поля и любого количества ступеней. При исполнении алгоритма Робот не должен разрушиться.

1. Выполните задание.

На бесконечном поле имеется лестница. Высота подъема лестницы неизвестна. Сначала лестница поднимается вверх, затем спускается вниз. Высота спуска также неизвестна. Высота и ширина каждой ступени – одна клетка. Робот находится под нижней ступенькой у левого края лестницы.

На рисунке указан один из возможных способов расположения лестницы и Робота. Робот обозначен буквой «Р».

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные под ступенями лестницы. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок):

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения лестницы. При исполнении алгоритма Робот не должен разрушиться.

Алгоритм может быть выполнен в среде формального исполнителя или  записан в текстовом редакторе.

Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

1. Выполните задание.

На бесконечном поле имеется лестница. Сначала лестница поднимается вверх справа налево, затем поднимается вверх слева направо. Высота каждой ступени – одна клетка, ширина – две клетки. Робот находится справа от нижней ступени лестницы.

Количество ступеней, ведущих налево, и количество ступеней, ведущих направо, неизвестно.

На рисунке указан один из возможных способов расположения лестницы и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно под ступенями лестницы, поднимающейся слева направо. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок):

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения ступеней внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

Алгоритм может быть выполнен в среде формального исполнителя или  записан в текстовом редакторе.

Сохраните алгоритм в текстовом файле. Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

1. Выполните задание.

На бесконечном поле имеется стена, огораживающая некоторый прямоугольник. В стене, являющейся нижней стороной прямоугольника, имеется проход шириной в одну клетку. При этом данная клетка не является крайней клеткой стены. Размеры стены неизвестны. Робот находится внутри огороженного прямоугольника, его точное расположение также неизвестно. Одно из возможных положений робота приведено на рисунке (робот обозначен буквой «Р»):

Напишите алгоритм, который перемещает робота вне огороженного прямоугольника, независимо от размеров прямоугольника и начального расположения робота. Например, после исполнения данного алгоритма робот может оказаться в следующей клетке:

Алгоритм напишите в текстовом редакторе и сохраните в текстовом файле. Название файла и каталог для сохранения вам сообщат организаторы экзамена.